结构分析时，常需在不同维度的向量空间之间进行数据传送，或实现维度扩张、收缩、矩阵初等变换等基本操作。为使用矩阵变换实现以上操作，本书特别定义了一类矩阵，称为数据传送矩阵（也简称为传送矩阵）。

如需要将一个n维向量X中第i个元素，送至m维向量Y中的第j个元素位置（仅空间维度扩充或缩减，物理量大小、性质均不变），可以使用矩阵变换的方式表达为：

此时的变换矩阵S（m×n），即为需构造的数据传送矩阵。构造传送矩阵时，除指定传送位置所对应于i行j列处sij=1外，其余元素皆为0。

式（1.2）的逆向空间变换，即将m维向量Y中第j个元素，变换传送至n维向量X中的第i个元素位置时，可利用前述传送矩阵S的转置运算来实现，即

在进行结构分析时，通过构造不同的传送矩阵，可容易地实现单元分析和整体分析间的数据传送、子块划分等基本操作。

1）单元和整体的数据传送

若n维子空间（如对应于单元，若设为3维）与m维空间（如对应于整体，若设为5维），在自由度之间的对应关系如下式：

子空间内单元向量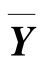对整体向量空间内向量Y的贡献可以用下式表达：

构造传送矩阵S时，可利用整体空间维度下单位阵，划除缺失自由度对应的列来得到。考虑FORTRAN中多维数组为按列存储，从程序编制调试的便利性出发，本书使用的传送矩阵为划列取得，读者若习惯使用其他程序语言，也可选用划行模式）。

而在单元空间内各向量间的变换矩阵，也可根据传送矩阵转换至整体空间内。若在单元空间两向量间存在变换关系：(www.daowen.com)

则变换矩阵对整体空间内变换矩阵A的贡献，可表达为：

2）矩阵的子块划分

若因算法需要，某矩阵A需拆分为4个子块，如下所示：

根据传送矩阵的性质，可构造

则有：

【说明】

结构分析时，在单元分析和整体分析之间需要传送大量数据；或因算法的需要，按一定规则进行矩阵的重排、切割，分析程序通常在此有大量语句，很难直接与力学概念对应，阅读难度大。

使用传送矩阵，利用矩阵线性变换进行数据传送，需要进行大量0元素的空操作，从算法的角度来看或许并非最优。但本书秉承结构分析中全过程线性变换的原则，在此处牺牲程序的计算效率，却可令程序编制过程简洁、易读、易理解、易修改，矩阵变换方式与结构化分析模块可直接全过程对应。

下面两段程序分别是：（1）利用定位向量集成总刚；（2）利用传送矩阵集成总刚的方式进行。显然，传送矩阵方式更能表达结构分析中的矩阵变换思维。