1.JRC抗力衰减摩擦抗力补偿模型原理

上述JRCW模型的过程其实是结构面内部JRC所提供的抗力逐渐衰减、摩擦抗力逐渐启动或增强的过程。目前，很多有关蠕变的试验表明，在蠕变状态下，具有非常显著的声发射现象，蠕变变形和试样内部裂隙的发生与扩展具有密切的联系［162 164］。蠕变应力保持不变，持续的能量输入导致结构面内部发生微破裂，JRC强度同样会不断降低，而随着蠕变变形不断增加，摩擦抗力也随之启动。

对于蠕变试验，JRC抗力衰减量要得到摩擦抗力的充分补偿才能维持试样稳定于蠕变应力，否则一旦摩擦强度无法补偿JRC强度的衰减量，结构面不能提供足够的抗力，内部抗力与外力不能平衡，那么试样便会发生破坏，即进入加速蠕变阶段。

2.JRC抗力衰减摩擦抗力补偿模型

根据式（4.4）可得蠕变（包括瞬时变形中的等效塑性变形部分）的等效塑性变形的表达式：

式中，Dci为起裂应力时的变形；Di－Dci为瞬时变形中的等效塑性变形，记为Dps，Dp－Dps为蠕变变形中的等效塑性变形，记为Dpc。

根据式（7.13），蠕变过程中JRC强度的衰减量为

式中，f（mmaxJRC，Dps）为瞬时变形时的JRC抗力。

蠕变应力τc为恒定值，为了维持蠕变应力的恒定，有下列不等式：

即蠕变过程中，试样中所能调动的摩擦抗力增量必须大于JRC抗力组分的衰减量，蠕变中才能表现出蠕变应力恒定的现象。

3.结构面剪切蠕变机理及破坏时间预测

（1）计算参数

以试验c -10 -6.52为例，对上述模型进行分析，根据第2章中直剪试验可得在JRC＝19、法向应力为6.52MPa时JRC衰减模型的参数，如表7.6所示，模拟结果见图7.22。

表7.6　计算参数（法向应力为6.52MPa）

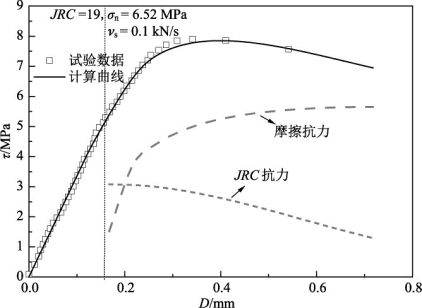
图7.22　结构面剪切曲线及计算结果

根据第4章的拟合结果及式（4.4），蠕变计算参数如表（7.7）所示。

表7.7　蠕变计算参数

（2）蠕变稳定及破坏解释

当剪切应力加载到蠕变应力时，由于变形速率不断减小，根据不同加载速率条件下剪切过程中（7.2.3节）摩擦抗力稳定临界变形Df与JRC抗力临界变形DJ的变化规律可知，加载速率减小，裂隙有足够的时间发育，不利于法向应力的传递以及摩擦强度的启动，摩擦抗力稳定的临界变形值Df增大，并且DJ和Df的差值增大，如图7.23所示，蠕变时摩擦抗力随塑性变形的发展速度低于剪切时摩擦抗力的发展速度，并且由于蠕变速率是不断减小的，Df也是动态变化的，JRC抗力的衰减是与裂隙发展及塑性变形Dp直接相关的，因而可以推测其变化不大。

当摩擦抗力始终大于JRC抗力需要补偿的强度时，结构面会一直保持稳定，而当摩擦抗力不足以补偿JRC抗力衰减的量值时，如果尚未达到摩擦强度最大值，摩擦抗力会随着蠕变速率的增大（加速蠕变阶段）而迅速增大，直到达到最大摩擦强抗力τf -max，摩擦强度不能再增大，外部应力大于结构面内部抗力，此时会发生蠕变破坏。因此，摩擦抗力形态会随着蠕变速率的变化而变化，摩擦强度的发挥会根据蠕变速率的大小而调整，判断蠕变稳定与否只需判断补偿抗力曲线是否大于最大摩擦抗力τf -max。

需要补偿的摩擦抗力曲线为(www.daowen.com)

式中，f（σntanφb，Dps）为瞬时加载至蠕变应力中的摩擦抗力组分。

根据试验参数（表7.6，表7.7）以及蠕变条件下等效塑性变形的发展规律［式（7.19），式（7.20）］，低蠕变应力状态下结构面的JRC抗力衰减以及补偿曲线如图7.23所示。当蠕变应力为4.9MPa，5.6MPa时，补偿强度曲线一直位于最大的摩擦强度下方，因此，摩擦抗力完全可以补偿JRC抗力的损失。因此，该应力状态下岩石一直处于稳态，不会发生蠕变破坏。

起裂应力以后摩擦强度不断增大，当蠕变应力较小时，摩擦强度与蠕变强度曲线相交，如图7.23中点A所示，该点摩擦抗力已经完全可以维持蠕变应力，外部应力与摩擦抗力平衡，因而此时裂隙不会发展，JRC抗力组分也不会下降，蠕变停止。

图7.23　蠕变中的强度损失以及补偿（长期强度以下）

同样地，当蠕变应力较高时，JRC抗力损失与补偿强度曲线如图7.24所示，参数Df也随着蠕变速率的变化而变化，以补偿JRC抗力的损失。但是需要补偿的抗力超过最大摩擦抗力时，结构面就会发生蠕变破坏，而临界状态下，补偿抗力曲线的强度值正好与摩擦抗力的最大值相等，即

如图7.24所示，当蠕变应力为6.3MPa，7.0MPa时，补偿曲线在图7.24中点B处与摩擦强度曲线相交，并且如果继续加载，则补偿曲线继续上升，逐渐大于摩擦强度，此时已经达到摩擦抗力极限，摩擦抗力组分不能对JRC抗力的衰减进行补偿，如图7.24中阴影部分，此时内部抗力不能与外部应力平衡，试样发生破坏。根据式（7.24）、式（7.22）和式（7.23）可预测其破坏时的等效塑性变形、蠕变变形以及破坏时间如下：当蠕变应力为6.3MPa时，等效塑性变形为0.77mm，蠕变变形为0.742mm，蠕变破坏时间为1 852h；当蠕变应力为7.0MPa时，等效塑性变形为0.54mm，蠕变变形为0.477 2mm，蠕变破坏时间为732h。

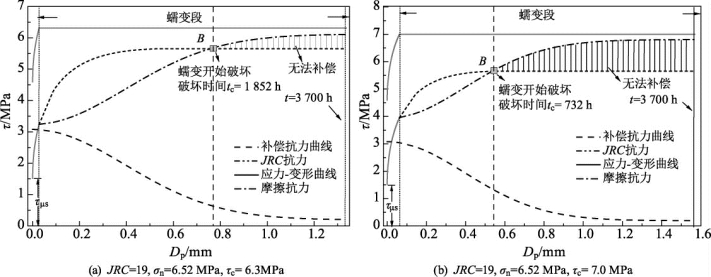
图7.24　蠕变中的强度损失以及补偿（长期强度以上）

从图7.24中可以看出，蠕变破坏时的蠕变变形以及破坏时间主要与以下两个因素有关：

（1）蠕变应力：结构面在高应力下发生蠕变破坏的时间比较短，蠕变变形也较小；反之，蠕变破坏需要的时间越长，蠕变变形也就越大。

（2）同一蠕变应力条件下，瞬时变形（初始变形）越大，蠕变变形越小，相应的蠕变破坏时间也就越短，即蠕变性质与瞬时加载段的应力路径有关。

4.结构面蠕变及松弛机理解释

根据上述论述，可将结构面看成不可回弹刚性体与摩擦片串联、与岩柱并联的物理模型，如图7.25所示，图中力学元件的性质如下：

①岩柱：表示JRC强度，该岩柱所能提供的强度在达到起裂应力之后会下降。

②刚性体：压缩时具有弹性的性质，但不具有回弹的性质。

③摩擦片：当该元件承担的应力低于摩擦片的阈值应力时，摩擦片不发生相对滑动，此时刚性体发生变形，而当该元件承担的应力高于摩擦片的阈值应力时，刚性体不发生变形，摩擦片发生相对滑动。摩擦片的阈值应力为τf max。

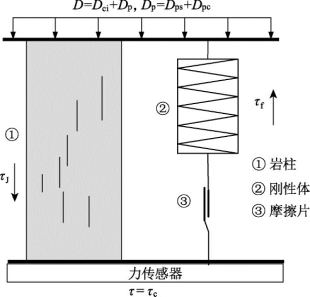
图7.25　蠕变机理

根据上述元件的基本特征，蠕变的机理可有如下解释：当结构面稳定在蠕变应力以后时，岩柱不断地破坏，造成了岩柱内抗力减小，同时由于蠕变变形的发展，刚性体所承受的应力不断上升，这时外部应力逐渐由岩柱转换到刚性体上承担。如果刚性体承担的应力小于摩擦片的启动阈值，那么此时内部抗力与外部应力平衡，摩擦片不会启动，结构面稳定。如果刚性体的应力大于摩擦片的启动阈值，则摩擦片启动，继而持续滑动导致大变形，如果一直维持大变形状态，外部应力无法降低，最终会引起结构面的破坏。

根据文献［165］中所述，固体材料在松弛时会产生声发射现象，虽然目前反映该现象的室内岩石试验结果还很少见，但是在现场试验中，李正旺等（2001）［166］在岩石隧洞的松弛区监测到了明显的声发射现象，上述现象表明，即使岩石的变形保持不变，在一定的应力条件下，岩石内部也同样会发生破裂。

如图7.26和图7.27所示，结构面加载至τri开始松弛，此时瞬时变形为D，保持初始变形不变，刚性体所产生的抗力恒定，但是在该应力条件下，岩柱内部出现裂隙，岩柱维持在该变形下所产生的抗力减小，此时外部并没有能量供给，系统底部所测得的应力减小，从而出现了应力松弛的现象。

图7.26　松弛在应力-变形曲线中的状态

图7.27　松弛物理模型