1.蠕变与应力松弛特征的联系

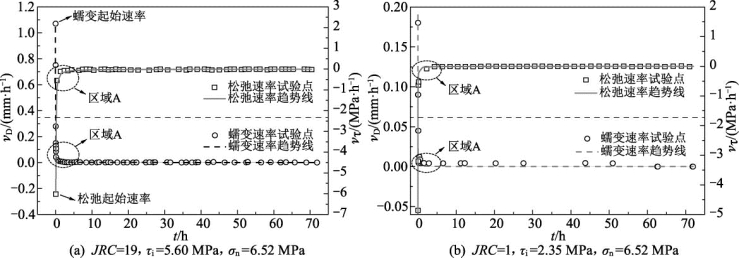
图7.1　蠕变速率与松弛速率关系图

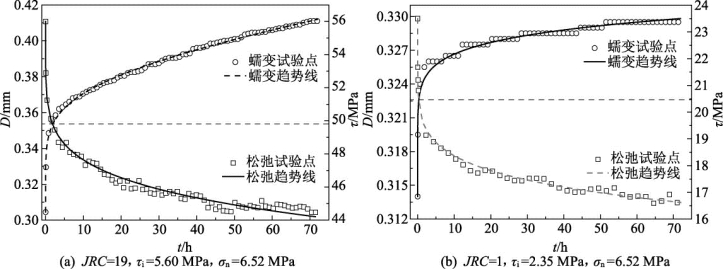
图7.2　蠕变曲线与松弛曲线关系图

如图7.1和图7.2所示，无论是蠕变曲线与应力松弛曲线之间，还是蠕变速率曲线与应力松弛速率曲线之间，都存在着近似的对称关系，它们随时间的变化规律基本相似，蠕变速率和应力松弛速率均表现出先迅速减小后趋于不变的形态。二者从形态上也非常一致，如两条曲线从迅速降低过渡到稳态阶段的时间基本相同（区域A）。这表明无论是蠕变还是松弛，蠕变变形或应力松弛的基本规律及相关曲线的形态是基本相同的。

2.蠕变与松弛之间的近似转换关系

根据本书第4章和第5章所推导的经验本构模型［式（4.1）和式（5.1）］可知，过渡蠕变段和稳态蠕变段蠕变速率及应力松弛速率可用以下表达式描述：

式中，vD为蠕变速率；nc为蠕变曲线形态及蠕变速率衰减速度的参数；mc为描述蠕变量大小的参数；vc为最终的蠕变速率；vτ为松弛速率；nr为描述应力松弛曲线形态及应力松弛速率衰减速度的参数；mr为描述松弛量大小的参数；vr为最终的应力松弛速率。

上述经验本构模型中，形式及参数均相同，通过第4章和第5章中对蠕变和松弛速率的拟合结果可知，两式均具有比较好的效果，并且由其推导得到的蠕变和松弛曲线可以很好地描述蠕变变形以及松弛应力随时间的变化。上述描述蠕变速率和应力松弛速率的本构模型可写作：

式（7.2）和式（7.3）相比可得：

(www.daowen.com)

对式（7.4a）中参数进行研究发现，如表4.6及表5.5所示，vc和vr为蠕变或松弛试验的最终速率，低应力下为0，高应力下该值也比较小，可近似为0，因而vc和vr的作用在式（7.4a）中可不考虑。因此式（7.4a）可转换为

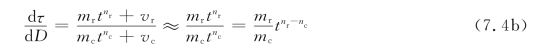
将式（7.4b）中的参数nr和nc进行对比，如表7.1所示，排除试样间的差异以及试验时不可避免的操作误差及环境差异，在同样的初始应力条件下，蠕变参数nr和应力松弛参数nc可以看作是相等的，也就是说，对曲线形态而言，二者具有相似性，这与图7.1和图7.2所反映的规律相同。进一步将式（7.4b）简化得到式（7.4c）：

从第4章和第5章中的参数研究可知，mc和mr分别是表征蠕变量与松弛量的参数，并且mc和mr分别与蠕变量和松弛量呈线性关系，mr／mc的物理意义是松弛量与蠕变量的比值。

表7.1　拟合参数对比

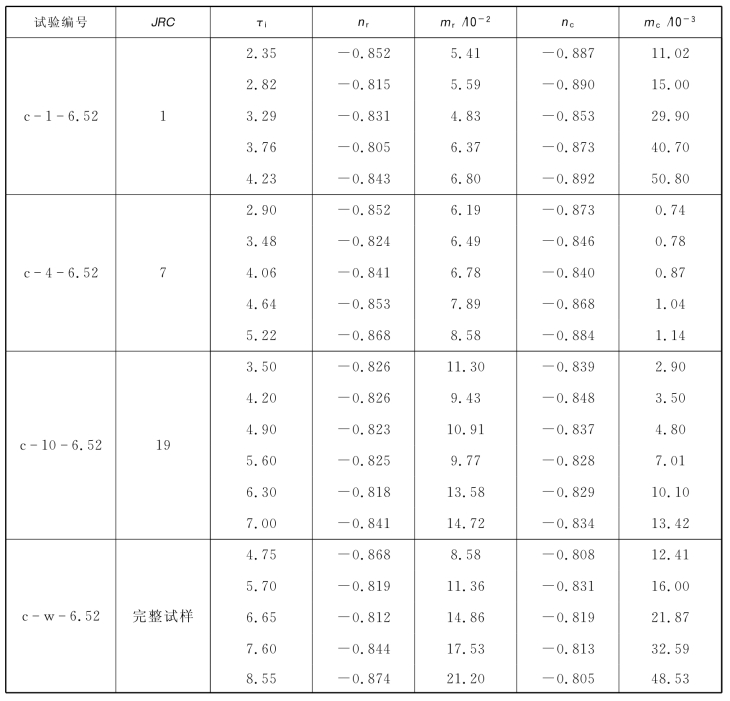
对mr和mc的关系进行研究，如表7.1和图7.3中所示，当JRC相同时，mr和mc表现出了较为明显线性关系，即

根据式（7.4a）和式（7.5）可知：

式（7.6）表示，同一初始应力下同样的结构面，经历相同时间后的松弛量和蠕变量（过渡蠕变阶段和稳态蠕变阶段）成正比。对于同一试样，在相同大小的初始应力条件下，δ为常数，并且为负值，表示蠕变变形增加时，应力减小。因此，蠕变与松弛之间是可以相互转换的，相等时间内松弛的应力与蠕变变形成正比，并且对于同一试样，该比值不随应力以及时间的变化而变化。

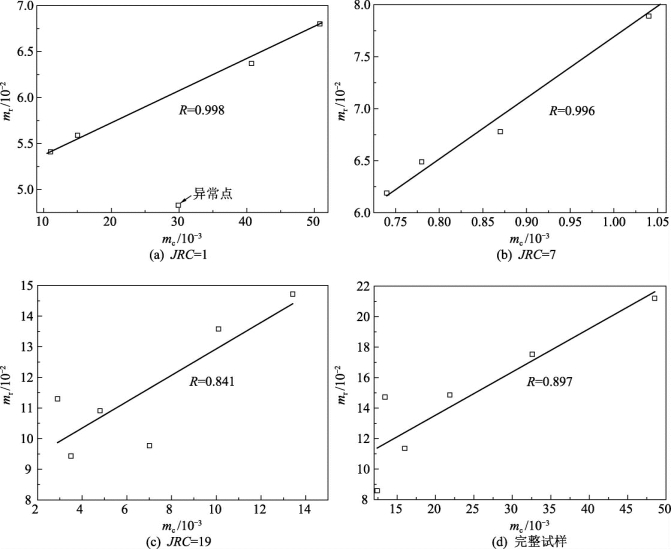
图7.3　mr与mc的关系