Goodman［31］提出蠕变与瞬时加载产生的应力-应变全过程曲线存在以下关系（图6.11）：长期强度以上的岩石蠕变破坏变形值，与瞬时全应力-应变曲线峰后同一应力下的应变量十分相近，即蠕变在应力水平稳定后的应力-应变轨迹是一条水平线（AB，CD，EF）。从点A或点C 开始的蠕变试验经过一段时间会在瞬时全应力-应变曲线峰后的点B或点D破坏，在临界应力水平点I以下点E开始的蠕变试验则经过很长时间才会逼近点F，而且不会引起破坏。轨迹线GH则是岩石试样在临界应力以下的各级荷载最终变形（如点F）连成的一条轨迹线。Bérest等［16］对这条曲线也做了相关的研究，将其称作极限变形轨迹。如图6.11所示，极限变形轨迹与全应力-应变曲线交于点H，在此荷载下经过长时间变形，能够与全应力-应变峰后段相交，这时的蠕变达到破坏所需要的时间最长，所需应力水平最低，破坏变形量也最大，因此，点H所对应的应力水平即为长期荷载下岩石不发生破坏的临界值，此应力值可作为长期强度。这个规律同样适用于岩石的疲劳试验，并且在葛修润［150，151］、章清叙［152］、肖建清［153］等人的试验中得到了证实（图6.12）。

根据极限变形轨迹的定义可知，极限变形轨迹具有以下特点：

（1）极限变形曲线的斜率（模量）一定低于任何加载速率下的斜率；

（2）极限变形曲线的形态与岩石性质有关，粗糙度较小时，相同应力水平下的变形较大，因而粗糙度较小时的斜率低于粗糙度较大时的斜率。

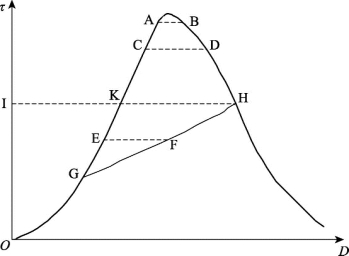
图6.11　蠕变与应力-应变曲线的关系(www.daowen.com)

图6.12　循环荷载下岩石的疲劳试验曲线与应力-应变曲线的关系

图6.13为不同JRC结构面剪切应力-变形曲线，随着JRC的增大，瞬时剪切的应力-变形曲线由磨损式到剪断式，即JRC＝0，1时，应力-变形曲线无明显的峰值，而JRC＝7，11，19时，随着对结构面“突起物”的剪切（即切齿）逐渐成为提供结构面抗力的一部分，并且所占的百分比增大，此时应力-变形曲线表现出较为明显的峰值，峰后则有很大的应力降。根据极限变形规律，极限变形曲线与应力-变形曲线交点所对应的应力值即为长期强度，那么不同应力-变形曲线的形态决定了交点的位置，进一步决定了长期强度与峰值强度之间的关系。如图6.13中极限变形轨迹所示，当应力-变形曲线没有明显峰值时（如JRC＝0），峰后曲线应力降较小，极限变形曲线与峰后曲线交于点J，此时点J的应力与瞬时剪切强度相差很小，这是由于时间作用强度降低的幅度较小。当应力-变形曲线峰值较为明显时（如JRC＝11），极限变形曲线与瞬时应力-变形曲线交于峰后的点G，该点的应力水平与峰值强度具有一定的差值，因而JRC越大，长期强度与峰值强度的比值越大。因此，根据瞬时应力-变形曲线形态及极限轨迹可以定性分析长期强度随JRC的变化规律。同样地，当法向应力增大时，瞬时曲线也表现出了类似的曲线特征，即法向应力越大，曲线峰值越明显，随着法向应力的增大，长期强度与瞬时强度的比值逐渐变小。

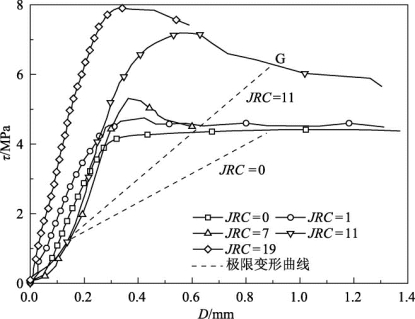
图6.13　不同JRC结构面剪切曲线与极限变形曲线