1.蠕变等速率曲线

蠕变曲线包括过渡蠕变阶段、稳态蠕变阶段和加速蠕变阶段等三个阶段，任何材料的蠕变均会经历第一阶段，只有应力大于长期强度时才会存在变形速率不为零的稳态蠕变阶段和加速蠕变阶段，否则当应变速率降至零时，蠕变停止，此时蠕变不会发生破坏［111］。因此，对于典型的蠕变曲线，在小于长期强度的应力水平下或加载时间较短的情况下，应变速率逐渐减小，各个时间点的速率在数值上不相等。在蠕变应力为τ（应力τ加载时间较短或小于长期强度）的蠕变曲线中，每个蠕变的时间点都对应着唯一的变形D和速率v。因此，可以利用（τ，D，v）三者之间一一对应的关系，先在蠕变速率的变化曲线上分别取不同荷载下速率相同的时间点，然后在蠕变曲线上求得该时间点的变形，利用取得的（τ，D，v）数值，在应力-应变坐标系中绘制出蠕变等速率曲线。蠕变等速率曲线的求解过程如图6.5所示［149］。

图6.5　蠕变等速率曲线的求解过程

根据上述方法，可得到9个试样的等速率曲线，以试验c -10 -2.17的曲线为例，取计算得到速率为0.000 6mm／h，0.000 5mm／h，0.000 4mm／h，0.000 3mm／h，0.000 02mm／h，0.000 01mm／h等6组数据绘制等速率曲线，如图6.6所示，曲线形态在图中拐点搜索范围内发生了变化，由线性关系转变为了非线性关系，具有较为明显的转折点，而该转折点标志着岩石黏塑性变形已经成为变形的主要部分。等应变速率曲线的力学意义是不同剪切速率条件下应力-变形关系的反映，当应力超过一定应力水平时，塑性变形或裂隙不稳定发展，其曲线形态也会发生变化［147，148］，如图6.6所示，每条等应变速率曲线都由近似线性段（黏弹性段）和非线性段（黏弹性＋黏塑性段）组成，并且具有明显的转折点，该转折点标志着岩石变形由黏弹性到黏塑性的转变，应力超过这个点以后，结构面内部裂隙开始不稳定发展，整个岩石发生破坏仅是时间问题，因此该转折点的应力水平是试样保持稳定不发生破坏的最大应力值，这与长期强度的概念基本相同，可以认为是长期强度。

图6.6　等蠕变速率曲线（试验编号：c -10 -2.17）

2.长期强度求解结果

根据上述分析，小于长期强度的蠕变等速率曲线应是近似线性关系（相对于非线性），而大于长期强度的蠕变等速率曲线形态为非线性。因此只需在已得出的蠕变等速率曲线中求得两段不同线型曲线的转折点（拐点）即可求得长期强度。为了避免由于人为选取拐点造成求解结果的主观性，将等速率曲线分为两段，即线性段和非线性段，利用Levenberg－Marquardt法，对曲线分段拟合，搜索可能的拐点，最后以非线性段在转折点的斜率与直线段的斜率差值最小作为判据，即两者斜率最接近于相等（差值约为0），求解拐点，其应力值即为长期强度。以试验c -10 -2.17速率为0.000 6mm／h的等速率曲线拐点的求解为例，在如图6.6所示的搜索范围内通过拟合寻找到9个拐点，在此拐点拟合的曲线R值均在0.999 9以上，线性段与非线性段的斜率差值随拐点应力的变化如图6.7所示，差值最小的点即为线性段和非线性段的拐点，图中斜率差值最小点的应力为2.782MPa，差值为1.568。根据以上方法，分别搜索图6.6中6条不同速率曲线的拐点值，结果如表6.5所示，最后得到平均值作为长期强度值，为2.79MPa。(www.daowen.com)

上述结果也证明，在低剪切速率下，速率变换对剪切曲线屈服点的影响不大。该方法求得的结果类似于求解曲线的屈服应力，但该屈服应力与常规剪切曲线的屈服应力不同，该方法求得的是低速率下的屈服点，长期强度与屈服应力的联系将在6.2.6节讨论。

表6.5　拐点求解结果

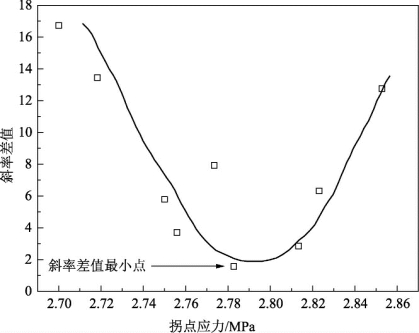
图6.7　斜率差值随搜索拐点应力值变化的曲线

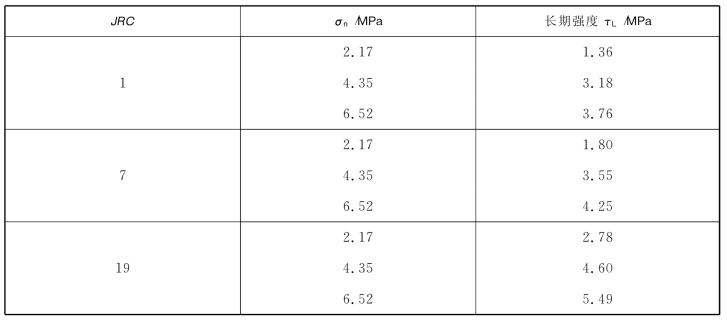
根据以上方法，表6.6中列出了通过分级加载蠕变试验以及等速率曲线拐点法求得的长期强度，长期强度值基本上符合过渡蠕变法所求得的长期强度范围（表6.4）。

表6.6　长期强度求解成果