与蠕变试验相同，对于应力松弛试验，主要关注以下两个方面：

（1）松弛应力的大小或剩余应力的大小。这是应力松弛的最终结果，是表示“松弛能力”的重要特征。

（2）松弛的持续时间或松弛速率的衰减速度。松弛速率衰减速度快，松弛持续时间较短，而当松弛速率衰减速度较慢时，松弛持续的时间则相对较长，此时从松弛到稳定状态也需要花费比较长的时间，该性质与试样材料及其本身的状态有关。

本节从松弛速率的特征出发，建立应力松弛速率与时间的经验关系，进而推导应力松弛本构模型，模型中的两个参数可直接反映上述两个方面的特征。

1.经验模型推导

如图5.10所示，结构面应力松弛速率的值随着时间的增加，逐渐减小，并且趋于稳定，该特征在曲线形态上与蠕变速率曲线基本相似。因而同样可以采用与蠕变速率曲线相同的表达式（5.1）描述其变化。

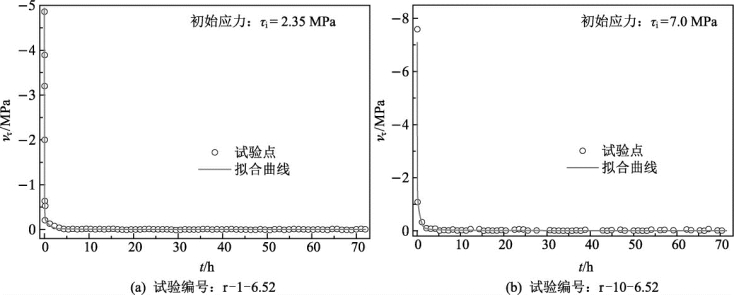
图5.10　应力松弛速率随时间的变化规律及拟合曲线

式中，vτ为松弛速率，vτ＜0，负号表示应力释放；t为松弛时间，t＞0；vr为t趋向于无限大时最终的松弛速率，vr＜0；mr，nr为拟合参数，mr，nr＜0；为速率衰减函数。

令，则

从式（5.2）中可以看出，应力松弛速率衰减量的自然对数与时间的对数呈线性关系，而nr反映了该函数衰减的速度，nr的绝对值越大，证明应力松弛速率衰减得越快，应力松弛进入第二阶段的时间也就越短，当nr的绝对值较小时，应力松弛第一阶段持续的时间越长，松弛速率衰减得越慢。

为了对式（5.2）的效果进行研究，以试验c -10-6.52中剪切应力为3.5MPa时的参数值作为基准参数，如表5.4所示，改变其中一个参数，保持其他两个参数不变，得到不同参数影响下的应力松弛曲线，如图5.11所示。由于速率变化较大，为了更好地表述松弛速率的衰减过程，图中的起始时间为1h。

表5.4　基准参数

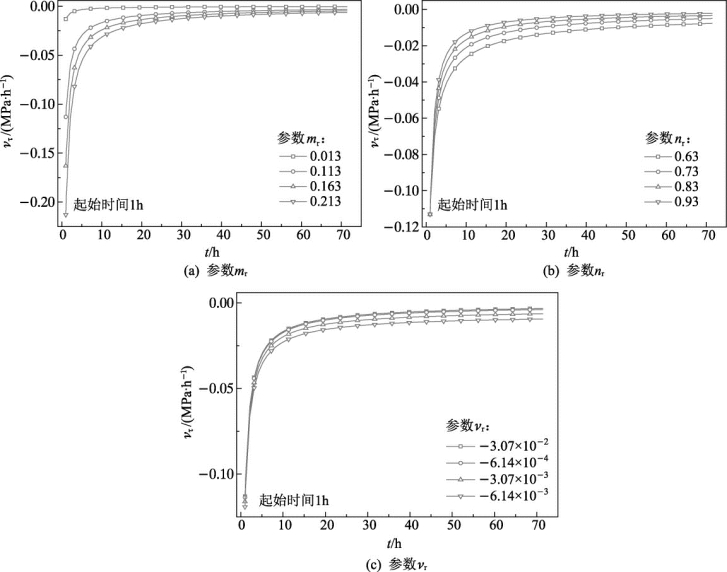
图5.11　各参数对应力松弛速率的影响(www.daowen.com)

从图5.11中可以看出，随着nr绝对值的增大，应力松弛速率随时间降低的速度更快，说明此时应力松弛速率很快衰减到了较低的水平，应力松弛达到稳定的时间较短，试样的应力松弛能力减弱，即抗松弛能力增强。

参数mr对应力松弛的影响主要表现在初始速率上，即衰减曲线的前半段上，由图5.11（b）可知，当mr的绝对值较大时，应力松弛速率的量值就较大，mr控制整个松弛速率的量级，但是衰减曲线的形状基本不变。

参数vτ对最终的应力松弛速率的影响较大，但其变化不影响整个曲线的形状。

式（5.1）可写成：

对式（5.3）进行积分可得：

式中，τi为积分常数，定义为应力松弛的初始应力。

利用式（5.4）对试验曲线进行拟合［图5.12（a），（c）］，并将拟合松弛试验曲线得到的参数用于求解应力松弛速率与时间的关系［图5.12（b），（d）］。无论是拟合还是参数反算的应力松弛速率曲线，都与试验数据接近，表现出了良好的拟合效果。

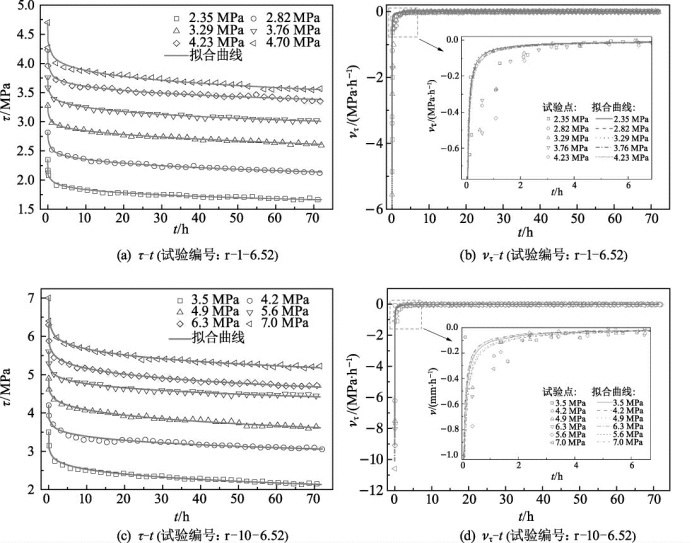
图5.12　应力松弛曲线（τ-t）及应力松弛速率曲线（vτ-t）拟合效果

2.经验模型参数分析

为了了解模型中各参数变化对应力松弛曲线的影响，对式（5.4）中的参数进行敏感性分析。基准参数仍然选取表5.4中的参数。如图5.13所示，参数nr、mr、vr对松弛曲线的影响如下：

参数nr的变化，改变了应力松弛曲线的形态，参数nr的绝对值越大，速率衰减得越快，即松弛曲线越快出现稳态松弛阶段，曲线快速进入稳态松弛阶段，并且稳态松弛阶段的斜率减小，即此时稳态松弛阶段的速率减小。

参数mr对曲线形态的影响并不大，主要影响松弛量的大小，其功能是将基准松弛曲线成倍地放大或者缩小，同时也影响松弛速率。mr越大，松弛速率的量级就越大，但不影响应力松弛曲线的基本形态。

参数vr主要影响稳态松弛曲线的斜率，在其他两个参数不变的情况下，参数vr越大，稳态松弛阶段的斜率就越大，相应的稳态松弛速率也就越大。

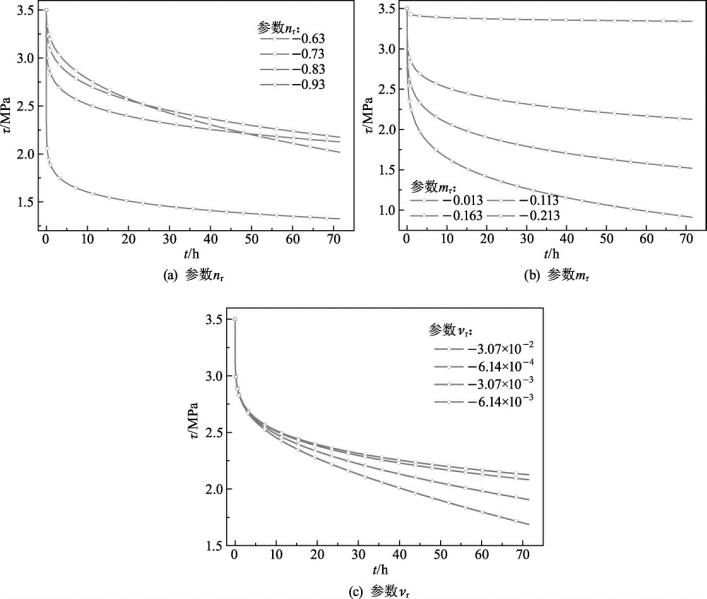
图5.13　应力松弛经验模型参数敏感性分析