虽然在实际工程中，加速蠕变阶段所引起的变形非常可观，并且直接导致工程岩体的不稳定甚至破坏，但是通过上述研究发现，一旦加速蠕变阶段开始，结构面会在较短的时间内破坏，并且一旦蠕变发展到加速蠕变阶段，变形已经相当可观。因此，研究蠕变前两个阶段的变形特征，将蠕变控制在前两个阶段，对于及早发现蠕变和预测蠕变的变形是非常必要的。

1.低应力作用下结构面蠕变变形－时间曲线特征

分级加载蠕变试验方法由陈宗基在波兹曼叠加原理的基础上提出的，也叫作陈氏加载法，如图4.8所示［141，142］，其基本原理如下：由于岩石对变形的记忆性，在分级加载试验第二级的试验过程中，变形增量包括第二级应力增量Δσ在Δt—2Δt时间内引起的蠕变变形ΔD0，ΔD1，ΔD2，…，以及第一级应力Δσ在Δt—2Δt时间内继续蠕变的变形ΔD2－1－t（下标“2”表示分级加载第二级，“1”表示第一级应力Δσ作用下在第二级时间内继续蠕变部分，t表示时间点），因而分级加载试验中第二级作用时间（Δt—2Δt）内的实际蠕变增量为ΔD2－t，（下标“2”表示分级加载第二级，t表示时间点）即根据波兹曼叠加原理可知，第二级应力一次性加载时在t时间内的蠕变变形为

即叠加后的变形等于第一级Δσ引起的蠕变变形与第二级Δσ引起的蠕变变形，反映在图4.8中即最终叠加后的曲线等于分级加载试验中第二级的实际变形量减去第一级荷载在Δt—2Δt时间内的蠕变变形。利用上述方法对分级加载蠕变试验的结果进行处理，可得到一次性加载蠕变曲线的处理方法。

图4.8　陈氏加载法及蠕变数据整理

图4.9所示为利用陈氏加载法还原后的蠕变曲线，各级应力下的蠕变曲线均表现出了较为明显的两个阶段：过渡蠕变阶段和稳态蠕变阶段，即蠕变起始时蠕变速率较大，蠕变变形发展较快，但随着作用时间的增加，蠕变变形的发展逐渐变缓，稳态蠕变阶段的线形虽然趋于线性，但稳态蠕变阶段的曲线仍然存在着非线性或波动的形态，因而传统意义上的稳态蠕变是着眼于蠕变曲线整体而言的概化分析，事实上，稳态蠕变速率仍然是有变化的并且有时会有比较明显的波动，随着能量的释放，稳态蠕变速率应是随着蠕变的发展而逐渐减小的。即稳态蠕变阶段的速率也应是逐渐减小的，只是在坐标系中由于速率变化较小，在有限的试验时间内，曲线近似趋于线性发展，此时可以近似认为蠕变速率是恒定的，在较高应力条件下，稳态速率保持一个较大的值，稳态阶段的蠕变变形曲线具有一定的斜率，而当剪切应力较小时，蠕变曲线在稳态阶段接近于水平，此时的稳态蠕变速率接近于0。根据曲线的特征可近似给出过渡蠕变阶段与稳态蠕变阶段的转换点，如图4.9所示，过渡蠕变阶段持续时间随法向应力、JRC以及蠕变应力的增大而增大。

图4.9　不同JRC及法向应力条件下的蠕变曲线

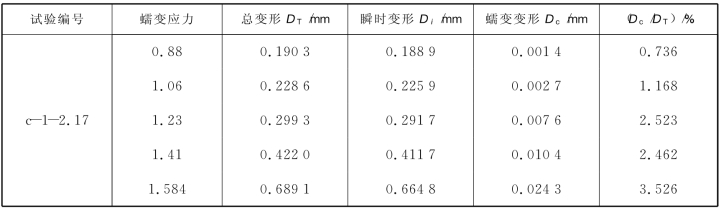
对叠加后的一次性加载蠕变曲线的变形量进行统计，如表4.3所示，随着JRC及法向应力的增大，蠕变变形在总变形中所占的比重是逐渐增大的，而瞬时变形量在总变形中所占的比重则逐渐减小，并且随着蠕变应力的增大，蠕变变形占总变形的比重逐渐增大。

表4.3　一次性加载蠕变变形统计

（续表）(www.daowen.com)

（续表）

2.蠕变速率变化特征

（1）初始蠕变速率变化特征

图4.10为法向应力为6.52MPa时，蠕变速率随时间的变化特征，图中蠕变速率为蠕变变形增量与时间增量的比值。

图4.10　蠕变速率变化特征（法向应力为6.52MPa）

由于初始蠕变速率往往非常大，如果速率变化跨度过大，在坐标系中不利于曲线形态的表达，因此取0.5h以后的蠕变速率数据，如图4.10所示，蠕变速率随应力的增大而增大，并且当应力水平超过某个级别时，蠕变速率会迅速增大，例如试验c－10－6.52在前三个应力级别下初始速率基本相等（相差不大），而当剪切应力为5.6MPa时的初始速率是4.9MPa时的1.68倍时，试验c－1－6.52和c－4－6.52也同样存在这样的规律，初始速率在3.76MPa和4.25MPa时均发生了较为明显的突变。

（2）稳态蠕变速率变化特征

根据全过程曲线特征的分析可知，稳态蠕变阶段的蠕变速率其实是一条近似线性的曲线，根据衰减蠕变持续时间的特征可知，在48～72h已经进入了稳态蠕变阶段，因而取48～72h的平均蠕变速率作为近似的稳态蠕变速率，如图4.11所示。当然，图4.11中低应力下的最终稳态蠕变速率应为0，但由于仪器的精度及控制过程中的误差，变形或蠕变速率仍然会有波动，计算出来的稳态蠕变速率是一个比较小的值，但不为0。高应力下蠕变速率一直处于减小的趋势，但是由于速率衰减得很慢，短期内可视为恒定的蠕变速率。这里为了研究稳态蠕变速率与蠕变应力及JRC之间的关系，仍然采用48～72h的平均速率为近似的稳态蠕变速率。

图4.11所示为每级近似稳态蠕变速率与各级应力的关系，以试验c－1－2.17为例，当剪切应力小于1.23MPa时（约为瞬时剪切强度的72%），近似的稳态蠕变速率基本上为0.6×10－5～1.4×10－5 mm／h，然而，当剪切速率超过1.23MPa时，稳态蠕变速率增大得很快，如当剪切应力由1.23MPa增大到1.41MPa时，稳态蠕变速率由1.4×10－5 mm／h增大至5.4×10－5 mm／h，因而在分级加载过程中，存在一个阈值，当应力超过这个阈值以后，稳态蠕变速率会急剧增大。稳态蠕变速率增大会造成蠕变需要更长的时间稳定，蠕变变形更大，发生蠕变破坏的可能性增大。稳态蠕变速率增大的原因是蠕变过程中裂纹的非稳定扩展或黏塑性应变速率的非线性增大造成的稳态蠕变速率的急剧增大［108］，而裂隙的不稳定扩展或黏塑性变形是造成结构面破坏、改变结构面力学性质的原因之一，因此，蠕变速率的变化也可作为判断长期强度范围的判据之一。

图4.11　不同JRC和不同法向应力条件下蠕变速率特征

不同的JRC和法向应力条件下，稳态蠕变速率随JRC和法向应力的增大而增大，例如JRC＝1，法向应力为2.17MPa，蠕变应力水平为90%时的蠕变速率为9.78×10－5 mm／h；当法向应力为6.52MPa，蠕变应力水平为90%时的稳态蠕变速率为16.23×10－5 mm／h，是2.17MPa时的1.65倍。而这种情况随着JRC的增大越来越明显，如JRC＝19时，法向应力为2.17MPa，蠕变应力水平为90%时的近似稳态蠕变速率为9.32×10－5 mm／h；法向应力为6.52MPa，蠕变应力水平为90%时的近似稳态蠕变速率为76.6×10－5 mm／h，是2.17MPa时的8.22倍。因此，当JRC及法向应力增大时，稳态蠕变速率增大。