图2.8中JRC与剪切强度的线性关系可用式（2.1）描述：

式中，参数m，n的值及其物理意义可由以下分析得到。

Barton和Choubey（1977）［34］提到的结构面抗剪强度经验公式如下：

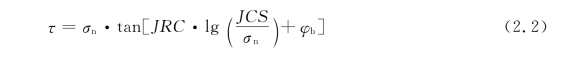
式中，φb相当于平整节理面的摩擦角；σn为法向应力；JCS为节理面壁的抗压强度。

根据式（2.1）和式（2.2）可得到以下分析结果：

（1）当JRC＝0时，仅为结构面材料间的摩擦强度，此时的强度等同于平整节理面的强度，即n可定义为

（2）当法向应力为0时，根据式（2.2）可知，此时无论粗糙度如何变化，结构面的抗剪切强度为0，式（2.1）中m表示抗剪强度随JRC的变化梯度，称为JRC的发挥系数。根据剪切强度随JRC的变化趋势可知，参数m与法向应力呈线性关系（图2.10），即

根据式（2.2）可知，当σn＝0时，结构面的剪切强度不随JRC的变化而变化，并且其强度值τ＝0，即式（2.4）中参数d＝0，即式（2.4）可写作：

图2.10中法向应力为0时，m是不为0的，这是试验中结构面差异及试验误差造成的。

对于相同的岩石材料，同一法向应力下参数m为定值。参数m随法向应力的增大而增大，这是由于法向应力的增大，结构面直剪强度组分的变化造成的，即法向应力越大，剪齿效应越明显，粗糙度发挥的作用也就越大，m值也就越大。

对于不同种类岩石材料的结构面，由于其材料强度以及结构面摩擦强度的差别，在剪切过程中各强度组分是不同的［26］，因此JRC发挥的程度也不尽相同，例如当岩石材料比较坚硬时，由于切齿比较困难，强度组分中摩擦强度所占比例大于剪齿强度，此时在同样的法向应力下，JRC的发挥系数m是不同的。因此，式（2.5）中的参数k是与材料相关的系数，参数k可由图2.8及图2.10获得。(www.daowen.com)

图2.10　参数m与法向应力σn的关系

根据上述分析，剪切强度与JRC的关系可写作式（2.6）：

式（2.6）中，剪切强度可以分为两部分，一部分与JRC相关，包括剪齿以及突起物表面的摩擦，即粗糙度贡献的强度——JRC抗力SJRC：

另一部分等同于摩擦抗力Sf，即

因此式（2.6）可写作：

即结构面的剪切强度由结构面内部两部分抗力提供：①与JRC有关的强度组分（JRC抗力）；②与摩擦相关（摩擦抗力）的强度组分。在直剪试验中，参数m或k的值可通过图2.8及图2.9获得，基本内摩擦角可由JRC＝0（即平板试验）时的剪切试验获得。因此对于本试验中的水泥砂浆试件，其强度与JRC的关系可写作：

不同法向应力及JRC结构面的剪切强度可由式（2.10）计算得到，如图2.11所示。计算结果基本符合试验结果的变化规律，并且计算值与试验结果接近。通过该表达式的计算，可基本反映不同JRC结构面的剪切强度变化规律。

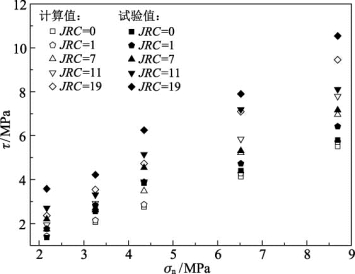
图2.11　计算值与试验值对比