统计降尺度方法是基于这样一种基本假设：区域气候是由当地的地理特性和大尺度气象状况所决定的。有鉴于此，区域观测气象变量（如降水量）和观测的大尺度气候因子之间的统计关系就可能建立。GCM模拟输出的关于大尺度的气候状况再联合这种统计关系，就能够降尺度到区域层次。基于MATLAB环境开发的统计降尺度模型ASD（Automated Statistical Downscaling Model）的结构简图见图10.2-1。

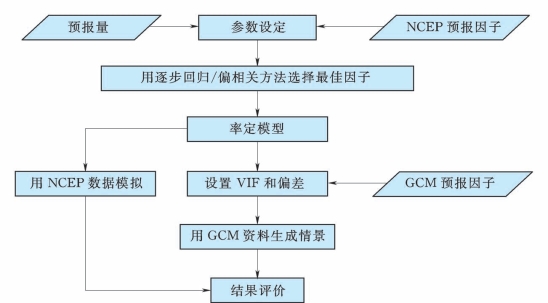
图10.2-1　ASD模型结构图

ASD模型可以在某一事件发生的条件下（如降水）或无条件下（如气温）运行。因此，日降水的模拟如式（10.2-1）所示，分为两个步骤：先模拟降水发生概率，如果有降水发生再模拟降水量。

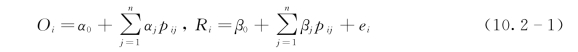
(www.daowen.com)

式中：O i为日降水发生概率；Ri为日降水量；p ij为预报因子；n为预报因子的数量；α，β为模型参数；ei为模型误差，并假设其服从高斯分布；Zi为服从正态分布的随机数；Se为模拟系列标准差；b为模型的模拟误差；V IF为方差放大因子。

利用NCEP预报因子率定模型时，b和V IF分别取0和12。将建立的模型应用到GCM排放情景时，b和V IF计算分别如式（10.2-3）和式（10.2-4）：

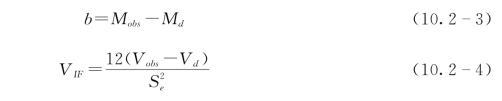
式中：M obs和M d分别为实测和模拟系列的均值；V obs和V d分别为实测和模拟系列在率定期内的方差；Se为标准差。

基于回归的降尺度方法一般采用多元线性回归，但是当预报因子之间的相关性很强时，会使回归系数的最小二乘法估计不稳定。因此，ASD模型提供了两种回归方法建立预报因子和预报量之间的统计关系，一般情况下采用多元线性回归，当预报因子之间有很强的相关性时，使用岭回归方法。该模型程序还具有将模拟的气候情景结果进行统计分析，制图输出等功能。