根据鄱阳湖入湖总入流1954—2007年54年洪水系列，进行洪水频率分析。

1.经验频率

在n项连序洪水系列中，按大小顺序排位的第m项洪水的经验频率P m，可采用下列数学期望公式计算：

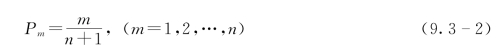
式中：n为洪水序列项数；m为洪水连序系列中的序位；Pm为第m项洪水的经验频率。

2.理论频率曲线线型

总入流洪水频率曲线线型采用P-Ⅲ型曲线。一维连续随机变量X的P-Ⅲ型分布具有如下的概率密度函数：

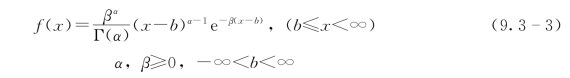
式中：Γ（α）为伽玛函数；α、β和b分别为分布的形状、尺度和位置参数。

3个原始参数α，β，b可以用基本参数数学期望值E X、变差系数（离势系数）Cv、偏态系数Cs表示如下：

用超过概率形式：

t=φp=φ（p，α）=φ（p，Cs），φ称为离均系数，有表可查，则频率曲线的纵标（设计值）为

皮尔逊Ⅲ型（P-Ⅲ型）分布参数，特别是Cs（或α）决定着密度曲线的形状，可以区分以下几种形状：

（1）当0＜α＜1，即∞＞Cs＞2时，密度曲线呈乙形，以x轴和x=b直线为渐近线，见图9.3-1（a）。

（2）当α=1，即Cs=2时，密度曲线退化为指数曲线，仍然呈乙形。但左端截止在曲线起点，该处的密度有限，右端仍延伸到无限，见图9.3-1（b）。

（3）当2＞α＞1，即2＜Cs＜2时，密度曲线呈铃形。左端截止在曲线起点，在该处与直线x=b相切，右端无限，见图9.3-1（c）。

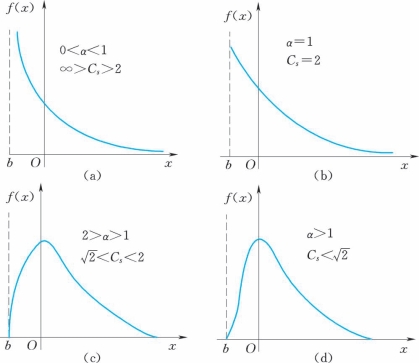
图9.3-1　P-Ⅲ型曲线不同形状

（4）当α＞2，即Cs＜2，密度曲线呈铃形。起点处曲线与x轴相切，右端无限，见图9.3-1（d）。

3.统计参数(www.daowen.com)

根据P-Ⅲ型统计参数样本平均值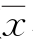、变差系数Cv和偏态系数Cs的定义，计算公式如下：

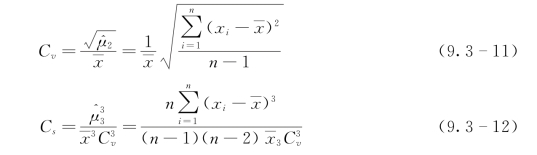
4.参数估计方法

采用由最小二乘法进行参数估计。最小二乘法又称离差平方和最小准则，常称最小二乘法。取经验点据与拟绘的频率曲线同频率纵坐标之差的平方和最小，其目标函数为

式中：f（P i，θ）为拟绘的频率曲线纵坐标P i，i=1，2，…，n；θ为统计参数x，Cv和C s；n为样本容量。

水文计算常用形式为

式中：φ为离均系数，是P i和C s的函数，有现成表可查用。

取目标函数极值最小，即

其解即为该准则（最小二乘法）的参数估计值。

由于式（9.3-13）、式（9.3-14）对θ（x，Cv，Cs）是非线性的，所以只能通过逐步迭代，求得参数的近似解。现已有计算机程序迭代求解。用矩法等参数估计方法的计算值作为初值，进行迭代计算，直至结果合乎精度要求。

估计了1d、3d、7d、15d、30d洪量的统计参数x、Cv、Cs，再进行适线调整。适线的原则为：长短时段洪量的参数基本协调，符合洪水统计参数的一般变化规律。适线成果见表9.3-2和图9.3-1～图9.3-6。

表9.3-1　鄱阳湖总入湖设计洪水成果表

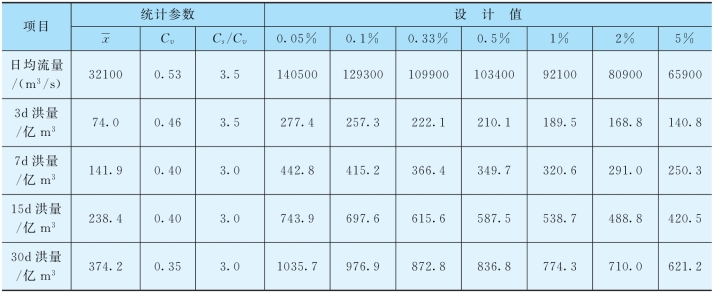
注 文献摘自《鄱阳湖水利枢纽项目建议书》（2010，10）。

图9.3-2　鄱阳湖总入湖最大日均流量频率曲线示意图

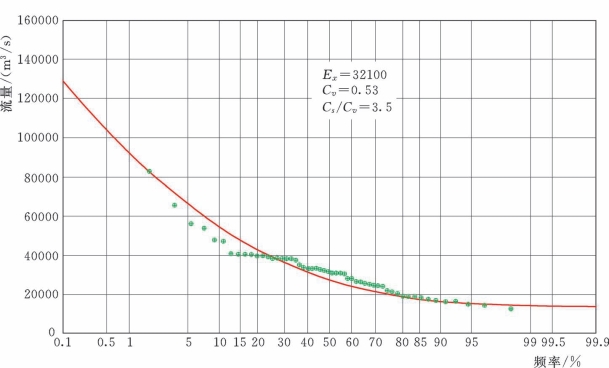
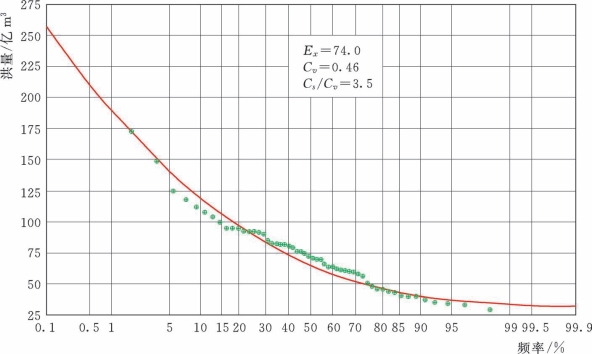
图9.3-3　鄱阳湖总入湖最大3d洪量频率曲线示意图