关于洪水的遭遇风险，目前常用的方法是根据研究区域历年同步洪水资料进行统计，只能对已发生洪水进行简单的统计分析计算，对发生百年一遇或千年一遇等设计洪水的遭遇风险尚无法定量估算。本章引入von Mises分布及其混合形式拟合年最大洪水（过程）发生时间、间隔时间，应用Copula函数分别构造汉口站和湖口站年最大洪水（过程）发生时间及二者年最大洪水发生时间（间隔时间）与其量级的联合分布，分析研究两站年最大洪水发生时间（间隔时间）及其量级在汛期每日的遭遇风险。

8.5.2.1 Copula函数简介

Copula函数是定义域为[0，1]均匀分布的多维联合分布函数，由Sklar定理，它可以将多个随机变量的边缘分布连接起来构造联合分布，对于二维来说，它可以表述为如下形式：

式中：C称为Copula函数，θ为Copula参数；F X（x）和FY（y）为随机变量X和Y的边缘分布。

Sklar定理是Copula函数构造联合分布的理论根据，它可以将联合分布分为边缘分布和相关性结构两部分，形式灵活，构造简单，使得Copula函数理论在水文及其他领域有了广泛应用。Archimedean Copula函数是水文领域应用比较广泛的一类Copula函数，它又包含Gumbel-Hougaard Copula、Clayton Copula和Frank Copula等函数形式。关于Copula函数形式及其选取和参数估计等一系列问题，文献已有详细介绍，此处不再赘述。

根据定义，洪水过程遭遇还需考虑洪水过程的量级，为与前面的洪水遭遇统计分析保持一致，选用7d洪量来反映洪水过程的量级，参考洪峰遭遇的分析方法，需要采用Copula函数构建洪水间隔时间与其量级的三维联合分布，这里首先对三维Copula函数做一简单介绍。

根据多维非对称Archimedean Copula函数的构造原理，三维非对称Clayton Copula的函数形式为

令F（x，y，z）为随机变量X、Y、Z的联合分布函数，则已知X=x时，Y、Z的条件概率分布函数为

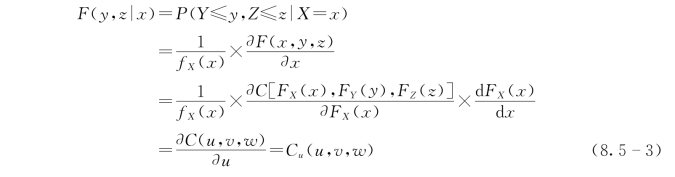
式中：u=F X（x），v=FY（y），w=F Z（z）分别为x、y、z的边缘分布。

8.5.2.2 von Mises分布及其混合形式

洪水发生时间（间隔时间）可看作是具有周期性变化的矢量，von Mises分布是描述具有周期性或季节性变量的常用分布，在医学、犯罪学等领域应用广泛，方彬等（2008）首次采用该分布拟合年最大洪水的发生时间，拟合效果较好。von Mises分布的密度函数为

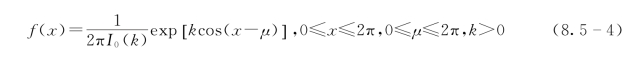
式中：μ和k分别为位置参数和尺度参数；I 0（k）为0阶变型Bessel函数。

如果洪水发生时间（间隔时间）呈现双峰特性（夏汛和秋汛），则可采用混合von Mises分布。混合von Mises分布由多个von Mises分布按一定比例相加而得，可以有效拟合变量的双峰或多峰特征，其密度函数为

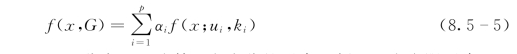
式中：f（x；u i，k i）为单一von Mises分布，αi为第i个成分的混合比例；p为有限混合von Mises分布的阶数，取p=2；G=（α1，α2，…，αp；u 1，u 2，…，u p；k 1，k 2，…，k p）包含所有参数。

8.5.2.3 年最大洪水遭遇的风险分析

1.年最大洪水发生时间

假定年最大洪水均发生于汛期，根据汉口和湖口两站1959—2009年汛期（5—10月）日径流资料，得到长江和鄱阳湖年最大洪水发生时间T C和T P两个序列。采用混合von Mises分布来拟合T C，采用von Mises分布来拟合T P。以上参数采用带有约束的极大似然法估计得到，如表8.5-5所示。

表8.5-5　参数估计结果

T C和T P的概率密度拟合如图8.5-5所示，可见，von Mises及其混合形式的分布能较好地拟合原序列。

图8.5-6绘出了长江和鄱阳湖年最大洪水在汛期每天相遭遇的风险。可以看出，两江洪水在6月之前遭遇的可能性很小，几乎为0，主要是因为长江汉口站的汛期一般在6—9月，滞后鄱阳湖一个月左右，因此，两江洪水一般不会在6月之前发生遭遇；两江洪水在7月16日遭遇的可能性最大，约为0.058%。其中6月末至8月初是两江年最大洪水发生遭遇的一个集中期，尤其是整个7月，每天遭遇的风险都在0.02%以上。

2.汉口站和湖口站年最大洪水发生时间和量级的联合分布

根据年最大洪水取样法，得到长江和鄱阳湖的年最大日均洪峰流量序列，经分析，两江发生年最大洪水的量级可看作独立事件。因此，两江洪水量级遭遇的风险为两江单独发生洪水的风险率之积，但这样得到的风险率仅为洪水在一年内遭遇的风险，如果两江洪水不是发生在同一天或时间间隔较大时，这样的洪水根本谈不上遭遇。为分析两江洪水量级在汛期每天发生遭遇的风险，引入中间变量——洪水发生时间，分别构造两江洪水发生时间和量级的联合分布，通过限定洪水发生时间便可以得到两江不同洪水量级在每天遭遇的风险。

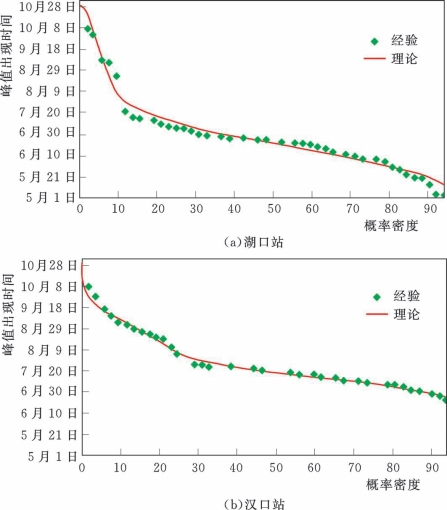
图8.5-5　长江和鄱阳湖年最大洪水发生时间概率密度拟合图

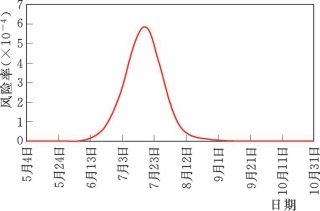
图8.5-6　长江和鄱阳湖年最大洪水发生时间的日遭遇风险(www.daowen.com)

3.汉口站、湖口站洪水年最大洪水量级遭遇风险分析方法

得到长江和鄱阳湖年最大洪水发生时间与其量级的联合分布后，就可以定义两江年最大洪水在第i天（ti）发生量级分别为q C和q P的风险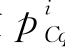q和p i

Pq为

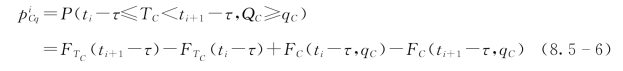
式中：τ为传播时间，这里取2d。

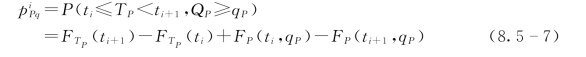
由于两江年最大洪水量级是相互独立的，因此，两江在某一天发生某一量级的年最大洪水也可以看作是独立的，则两江洪水量级在第i天遭遇的风险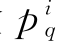为

同理，将汛期内两江某一量级洪水的日遭遇风险相加，得到整个汛期的洪水遭遇风险：

据此就可以计算两江洪水各种量级（同频率或非同频率）在汛期每日的遭遇风险。

8.5.2.4 洪水过程量级遭遇的风险分析

1.七天洪水过程间隔时间的特征分析

按年最大取样，得到长江和鄱阳湖年最大7d洪量W 7，C和W 7，P及其间隔时间序列T d，取2阶的混合von Mises分布描述间隔时间的分布特征，参数估计结果u 1=2.64，k 1=3.40。拟合结果如图8.5-7所示，可见拟合效果较好，图中负号表示鄱阳湖洪水先于长江发生。由此可知，当纵坐标T d=-178时，意味着鄱阳湖年最大7d洪量发生于5月1—7日，长江最大7d洪量在10月25日之后发生，其概率为0；当T d=178时，即长江在5月1—7日洪量最大，鄱阳湖在10月25日之前出现年最大7d洪量，其概率为1，频率曲线呈现两端有限的趋势，这与之前的假定年最大洪水全部发生于汛期相吻合。T d=0时，对应的概率值为19.23%，意味着长江先于鄱阳湖发生年最大7d洪水的概率为19.23%，也即鄱阳湖先于长江发生年最大7d洪水的概率为80.77%，表明一般情况下，鄱阳湖先于长江发生年最大7d洪水，在气候成因上符合长江流域洪水发生的一般规律。

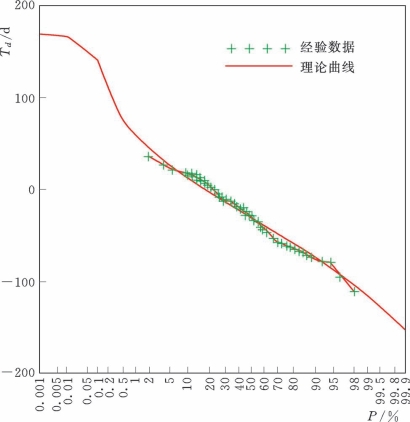
图8.5-7　长江和鄱阳湖年最大15d洪水间隔时间T d的频率曲线

由洪水过程遭遇的定义可知，间隔时间T d∈[-4，4]时，两江年最大7d洪水有4d及以上重叠，概率为7.31%，即两江洪水过程遭遇的概率为7.31%。其中T d∈[-4，0]的概率为4.30%，T d∈[0，4]的概率为3.82%，也即在两江7d洪水过程遭遇的情形下，鄱阳湖先于长江出现年最大7d洪水的概率为4.30%，长江先于鄱阳湖的概率为3.82%。

2.联合分布

长江和鄱阳湖年最大洪水发生量级与其间隔时间之间存在一定的相关性，根据Copula函数构造联合分布的方法和步骤，建立两江年最大7d洪量W 7，C和W 7，P与其间隔时间T d的联合分布，联合经验频率拟合图见图8.5-8。其中，间隔时间服从混合von Mises分布，7d洪量服从P-Ⅲ分布。参数估计的结果见表8.5-6。

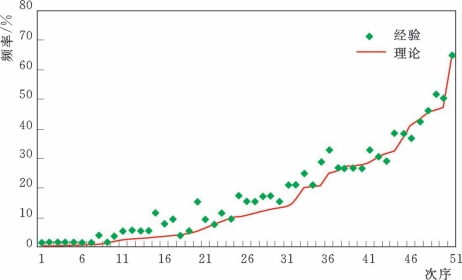
图8.5-8　长江和鄱阳湖年最大7d洪量与其间隔时间的联合经验频率拟合图

表8.5-6　P-Ⅲ型分布的参数估计结果

根据Copula函数的选取原则，采用Clayton Copula函数构造洪水间隔时间和量级的联合分布，统计参数由极大似然法估计而得：θ1=0.1，θ2=0.5。则长江和鄱阳湖年最大7d洪量与其间隔时间的联合分布函数为

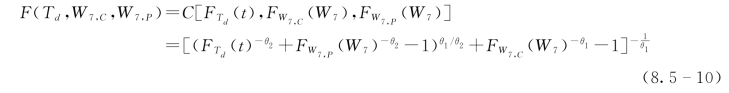
3.七天洪水过程遭遇的风险分析

得到长江和鄱阳湖年最大7d洪量与其间隔时间的联合分布后，就可以根据前面洪水过程遭遇的定义，得到两江洪水过程遭遇的风险为

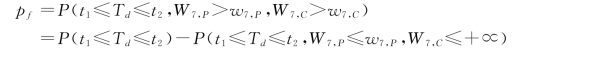
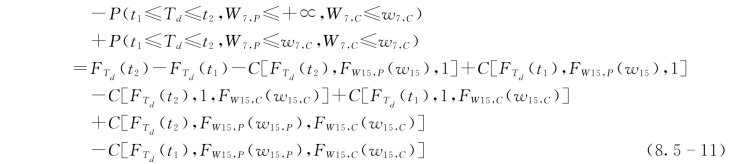
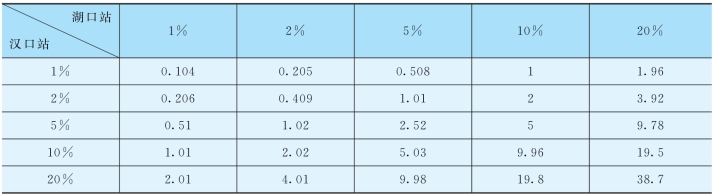
当T d∈[t 1，t 2]=[-4，4]时长江和鄱阳湖洪水过程才会遭遇。便于日后的查询，制作了几种设计频率组合下的遭遇风险表，如表8.5-7所示。对于实际中出现的遭遇组合可以通过内插进行估算。

表8.5-7　长江和鄱阳湖7d洪量不同频率遭遇的风险率（×10-4）