1.博阳河流域

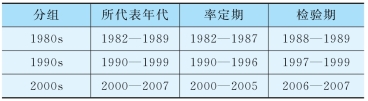
将1982—2007年的资料分为3组，即：1982—1989年、1990—1999年和2000—2007年，分别以1980s、1990s和2000s代表这三个时期。三个时期分别率定和检验，以区别模型在不同时期的适用性，各组率定期和检验期的划分如表5.2-2所示。

表5.2-2　 博阳河流域资料分组及率定期和检验期

按照建立VIC模型的步骤，将大气强迫资料（包括降雨、最高和最低气温）、土壤和植被资料输入模型，在博阳河流域以子流域为计算单元进行计算。在运行VIC模型时，为观察模型各参数的特性，采用人工调试的方法进行参数优选。各时期优选的模型参数如表5.2-3所示。

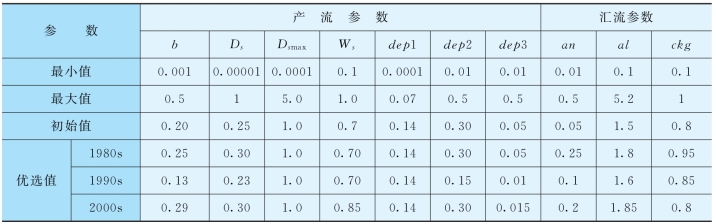
从表5.2-3所列的各时期模型参数来看，10个参数中，以Dsmax和dep 1最为稳定，均为1.0和0.14，其余各参数变动不大，可根据这些参数的变动规律，进一步缩小参数范围，为下一步进行未控区间流域的参数移植提供依据。

表5.2-3　博阳河流域VIC模型参数值

如表5.2-4所示，VIC模型在三个时期的模型效率系数相差不大，均在85%以上，达到了国家《水文情报预报规范》（GB/T 22482—2008）的甲级标准。虽然径流总量相对误差在不同时期略有不同，但是误差范围均控制在5%以内，其中以1980s时期的径流量模拟效果最好，基本上与实测值趋于一致。2000s时期径流总量相对误差略微偏大，率定期和检验期分别为4.45%和2.82%，模拟径流量比实测值偏大。1990s时期的模拟效果无论是径流量还是流量过程线均与1990s时期相近。

表5.2-4　博阳河流域VIC模型率定和检验结果

采用遗传算法对新安江模型参数进行优选。该算法对初值并不敏感，参考新安江模型应用的文献，在合理的参数范围内任意设置初始值，并对各个时期给出相同的参数值的取值范围，最大迭代次数设置为6000次，基本上可以得到较为稳定的近似最优值，各时期优选的模型参数列于表5.2-5。

表5.2-5　博阳河流域新安江模型参数值

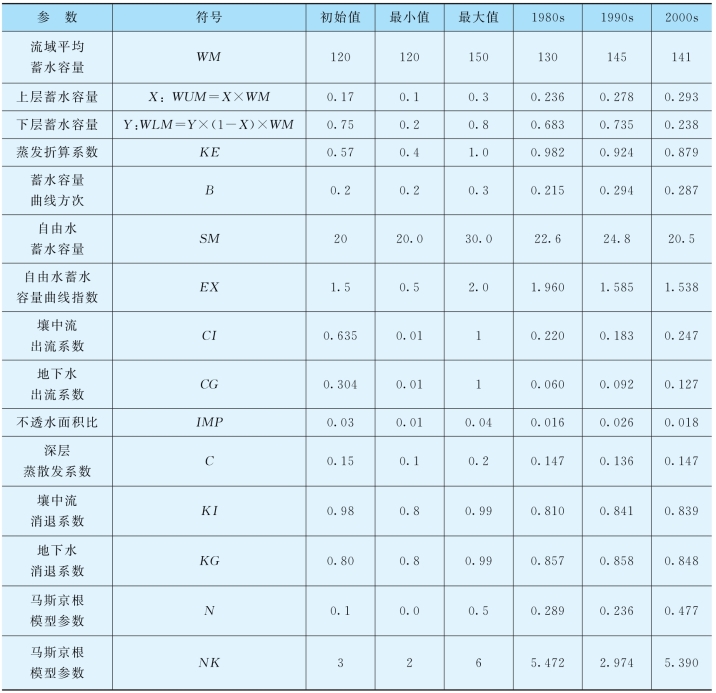
从表5.2-5中可以看出，采用自动优选的方法得到的模型各参数，在不同时期变动不大，其中地下水消退系数KG基本上在0.85左右，深层蒸散发系数C基本上在0.14左右。1990s和2000s时期的流域平均蓄水容量WM、蓄水容量曲线方次B比较相近，分别在140和0.29左右。1980s和2000s时期的不透水面积比IMP、马斯京根模型参数NK比较相近，分别在0.17和5.4左右。

如表5.2-6所示，新安江模型在1990s应用效果最好，效率系数在率定期和检验期分别达到80.33%和87.22%，达到国家《水文情报预报规范》（GB/T 22482—2008）乙级标准，且径流总量相对误差均在5%以内。1980s应用效果其次，率定期模型效率系数为80.79%，检验期稍差，为68.73%。2000s时期模型应用效果较差，模型效率系数分别为71.87%和67.64%。总体看来，新安江三水源模型在博阳河流域的应用，虽然模型效率系数在各时期不尽相同，但是各时期径流总量相对误差的绝对平均值为3.45%，处于相对理想的范围。

表5.2-6　博阳河流域新安江模型率定和检验结果

Top Model模型是以地形为基础的水文模型，地貌指数分布曲线是其中非常重要的一个输入。图5.2-6列出了博阳河流域填洼前后的地貌指数分布曲线。对比看来，填洼后的曲线相比填洼前的曲线显得扁平，面积比例的最大值有所降低，地貌指数分布更加均匀。

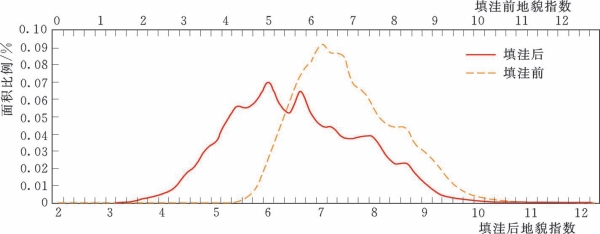
图5.2-6　博阳河流域填洼前、后的地貌指数曲线

采用单纯型法优选Top Model模型参数。单纯形法不是直接去探查有利方向，而是求出单纯形各个顶点的目标函数值，并加以比较，丢掉目标函数值最大的点，代之以新点，如此构成新的单纯形，通过这种方式逐步逼近极小点。博阳河流域Top Model模型优选的参数列于表5.2-7，如表所示，模型中所需要优选的6个参数值在各时期的值差异较大，并没有显示出一致的规律。

表5.2-7　博阳河流域Top Model模型参数优选值

如表5.2-8所示，Top Model模型在3个不同时期率定期的模型效率系数在69.40%～77.38%之间，检验期相对较差，除1990s为73.15%外，另外2个时期在55%左右。径流总量相对误差对于1980s和1990s时期，率定期不超过2%，而检验期却达到了8%左右；2000s时期径流总量较实测值偏大程度在率定期和检验期均达5%以上。

表5.2-8　博阳河流域Top Model模型率定和检验结果

从图5.2-7～图5.2-12列出了3个时期的实测和Top Model模拟流量过程线，从中对比可以看出，Top Model对流量过程能大致地模拟，特别是在流量较小时，能较好地拟合，但是对洪峰流量的模拟值在大多数情况下都偏低，这可能就是导致模型效率系数低的原因。

2.西河流域

根据前述小节的资料分析，目前西河流域仅收集到1971—1976年共6年比较完整的资料，因此以1971—1974年为率定期，1975—1976年为检验期，研究各模型在西河流域的适应性。

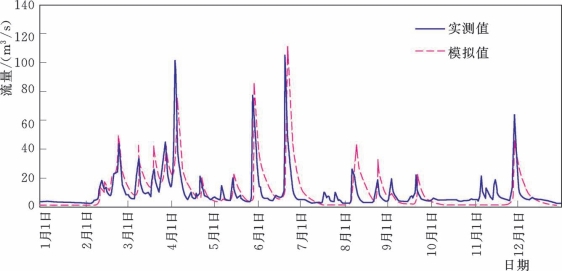
图5.2-7　博阳河流域1982年实测和Top Model模拟流量过程线（率定期）

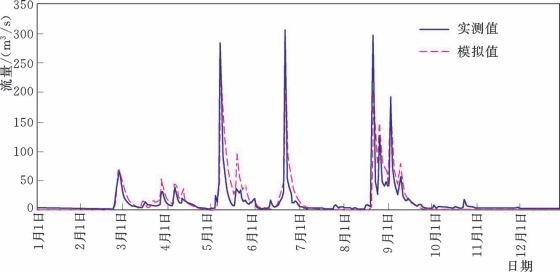
图5.2-8　博阳河流域1988年实测和Top Model模拟流量过程线（检验期）(www.daowen.com)

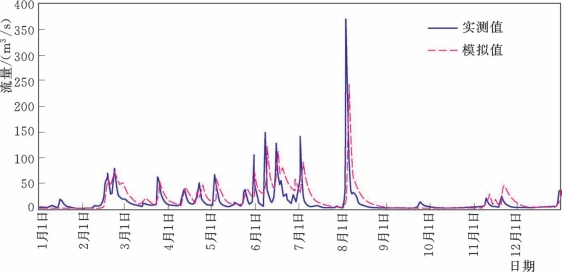
图5.2-9　博阳河流域1990年实测和Top Model模拟流量过程线（率定期）

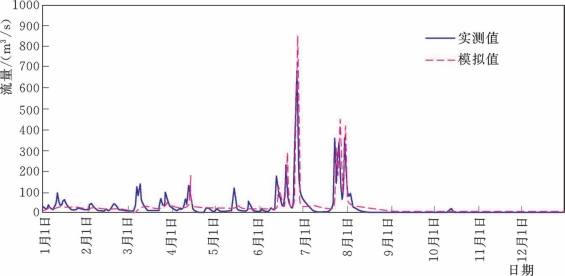
图5.2-10　博阳河流域1998年实测和Top Model模拟流量过程线（检验期）

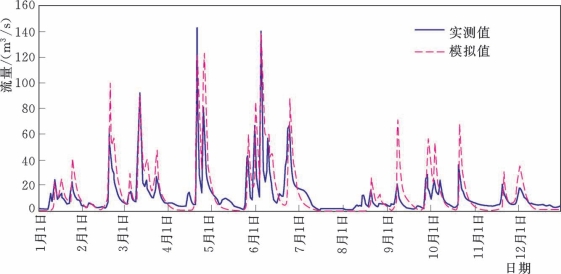
图5.2-11　博阳河流域2000年实测和Top Model模拟流量过程线（率定期）

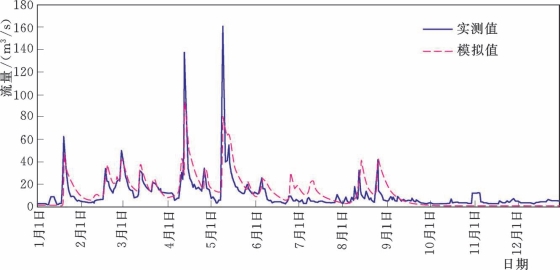
图5.2-12　博阳河流域2006年实测和Top Model模拟流量过程线（检验期）

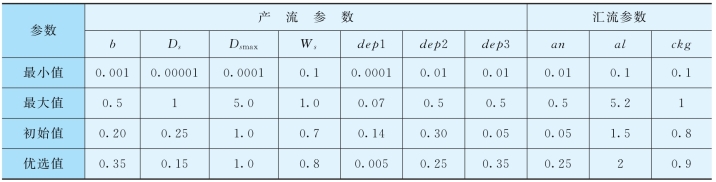
同博阳河流域类似，西河流域VIC模型参数率定结果列于表5.2-9。

表5.2-9　西河流域VIC模型参数值

如表5.2-10所示，VIC模型在西河流域率定期的模型效率系数达到71.32%，检验期不甚理想。径流总量相对误差在率定期和检验期分别为-0.02%和-1.32%，说明该模型对西河流域的径流量模拟有一定适应性。

表5.2-10　西河流域VIC模型率定和检验结果

在西河流域应用新安江模型时，输入1971—1976年的降雨、蒸发以及实测流量数据，采用遗传算法进行参数自动优选。优选的参数值如表5.2-11所示。

表5.2-11　西河流域新安江模型参数值

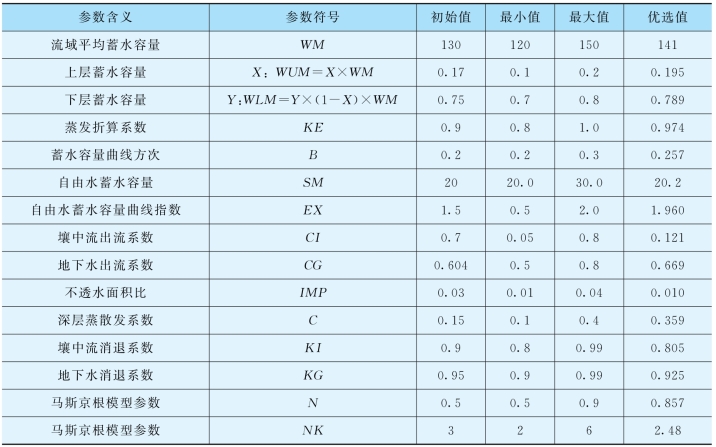
表5.2-12列出了新安江模型在西河流域率定和检验结果，表中结果显示，模型效率系数在率定期和检验期均在60%左右，但是径流总量相对误差无论是在率定期还是检验期绝对值均不超过5%，说明新安江模型对西河流域的径流量模拟具有一定的适用性。

表5.2-12　西河流域新安江模型率定和检验结果

如图5.2-13所示，西河流域的地貌指数分布曲线在填洼前后的变动相比博阳河流域并不明显。运用Top Model计算时，采用填洼后的地貌指数分布曲线作为西河流域Top-Model模型的输入。

与前面的VIC模型和新安江模型的输入一致，参数优选方法同样采用单纯型法，优选的模型参数列于表5.2-13。

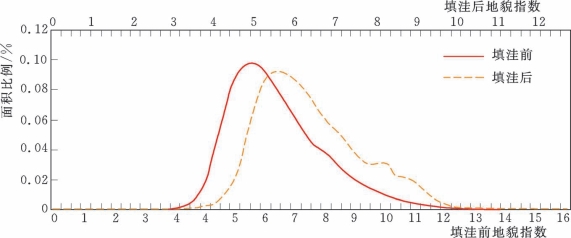
图5.2-13　西河流域填洼前后的地貌指数分布曲线

表5.2-13　西河流域Top Model模型参数优选值

西河流域Top Model模型在1971—1976年的率定和检验结果如表5.2-14所示。模型效率系数在率定期和检验期非常接近，均约为60%，径流总量相对误差在率定期和检验期分别为12.52%和5.12%，略显偏大。

表5.2-14　西河流域Top Model模型率定和检验结果

类似于Top Model模型在博阳河流域的应用情况，如图5.2-14和图5.2-15所示，Top Model模型对于流量过程的波动趋势能够较好地模拟，但是洪峰流量在实测值和模拟值之间相差较大。

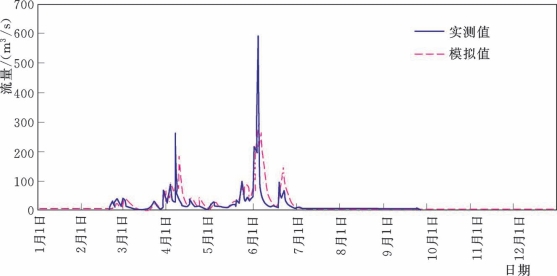
图5.2-14　西河流域1972年实测和Top Model模拟流量过程线（率定期）

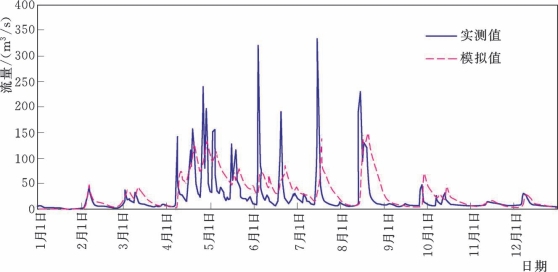
图5.2-15　西河流域1975年实测和Top Model模拟流量过程线（检验期）