通过对分洪溃口水量及水文测验方法的分析，鄱阳湖区间有些年份水量不平衡的现象可以得到修正。如1962年，采用水文站实测资料计算的湖区陆面产流系数为0.98，该年6月赣江下游发生大洪水，丁家渡水文站以上多处圩堤决口，据推算由于决堤影响未通过丁家渡测流断面而直接进入湖区的水量约为89.2亿m3，据此可计算出1962年湖区径流系数（陆面）为0.64，已经在合理的范围内了。

湖区区间地形一般较为复杂，湖汊、洲滩较多且分布较为分散，不同类型下垫面的洪水难以用一个集总型模型对其产汇流进行模拟。新安江模型是由原华东水利学院（现为河海大学）赵人俊教授等提出来的。从降雨径流经验相关图研究开始，经历了20多年形成了蓄满产流概念、理论及其新安江二水源模型之后，于1984年提出了新安江三水源模型，并在水文模拟和洪水预报中大量应用，在湿润地区和半湿润半干旱地区都取得了良好的应用效果，被联合国教科文组织列为国际推广模型而广为国内外水文学家所了解和应用。针对湖区降雨分布、下垫面较为复杂及湖泊调蓄影响显著等特点，本书中采用了几种不同计算方法，对湖区产汇流规律进行探讨，并对不平衡年份的汛期区间水量进行了分析计算。

4.3.4.1 新安江三水源模型

1.模型介绍

新安江模型是一个分散性模型，将产流区按陆面和湖面等分成多块，对每块单独进行产流和汇流计算，并模拟各块的出流过程，然后经河网汇流演算，总和后求得整个流域出口断面的流量过程。新安江模型较为符合鄱阳湖区气候和下垫面条件，被选择进行湖区水资源量的模拟计算。

新安江三水源模型主要由四部分组成，即蒸散发计算、蓄满产流计算、流域水源划分和汇流计算。二水源模型是按Horton产流理论用稳定下渗率把总径流划分成超渗地面径流和地下径流，而三水源模型是采用自由水蓄水水库把径流划分成地面径流、壤中流和地下径流。地面径流汇流计算一般采用单位线法，壤中流和地下径流汇流计算采用线性水库法。新安江三水源模型的流程图如图4.3-5所示。

新安江模型的核心是两条曲线：一条是蓄水容量曲线，表示降雨分布均匀时的产流面积的变化情况；另一条曲线是自由水容量曲线，控制径流的组成和分布，进行水源划分。

2.新安江模型计算湖区水量

鄱阳湖区间计算面积约25082km2，根据湖区下垫面特点及降雨特性，将全区间划分为陆面和湖区（以22.00m高程为界）两大部分。其中以河流水系为单元将沿湖泊四周分布的陆面部分划分为13块，并计算出每块所占权重。同时，根据各单元至出湖远近，分别确定各单元至湖口汇流河段数。湖区分布为湖泊区和变动回水区（包括民圩区）。本次考虑湖泊区受水位变化影响，依据其变化分变动水面和变动陆面计算。一般情况下，圩区按陆面计算，若大水期间有大圩溃决，则可据圩区H～A曲线，与湖泊区一样划分为变动水面和陆面。

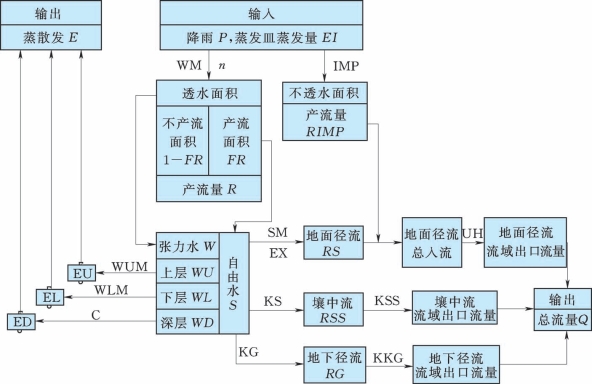
图4.3-5　新安江三水源模型结构图

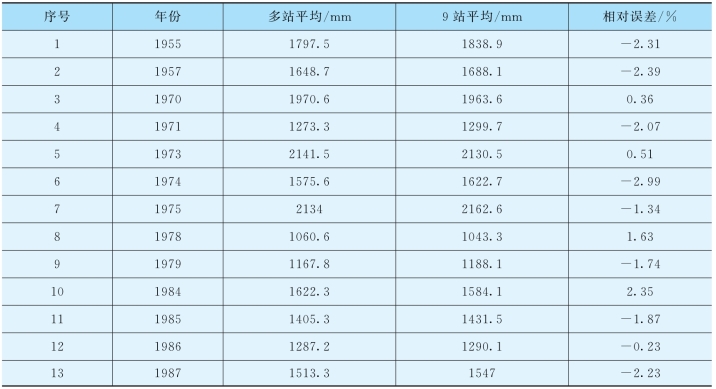
（1）雨量站代表性分析。鄱阳湖区间面积较大，区间内雨量站较多，约有50个雨量站点。分析计算时仅选取了外洲、李家渡、梅港、虎山、渡峰坑、波阳、柘林、万家埠和都昌等9个雨量站作为整个湖区分析计算的代表站，为分析这些雨量站的代表性，特选取1955年、1957年、1987年等13个年份，分析多站及9站的平均年降雨量的差异，结果见表4.3-5。表中结果显示，选取的13年资料中，年降雨量有大有小，多站平均与9个代表站的均值之间相差较小，说明所采用的9个雨量站资料具有较好的代表性。

表4.3-5　鄱阳湖区间雨量站代表性分析结果表

（2）模型参数的率定。新安江模型属于概念性模型，其参数都具有明确的物理意义。本次计算采用经验方法来估计模型各参数初始值，选取湖泊区间内具有实测资料较为完整的小流域初步拟定参数。选定的代表性流域仍为博阳河内梓坊站控制的流域。优选参数时，以径流量、洪峰流量及对应时间指标为目标，初步优选出模型参数。由于各单元的面积变化幅度在1000～3200km2范围内，与梓坊站的控制面积626km2相差不远，可将其初步移用于湖泊区间其他单元。

初拟模型参数后，再选取整个湖泊区间水量相对平衡的年份，以降雨量、蒸发量作为输入，用模型计算产汇流过程，与实测过程进行比较，以水量误差最小为原则，确定模型参数最优值。

率定参数的年份选取1959年、1966年、1970年和1976年4个典型年，计算时段取汛期4—8月。4个年份中汛期降雨量有大有小，基本考虑了降雨量的不同量级情况。为检验所率定的参数，又选取汛期降雨量一大一小的1969年和1972年两个典型年作为检验参数的年份。新安江三水源模型率定及检验的成果，见表4.3-6。

表4.3-6　率定新安江三水源模型参数成果表（4—8月）

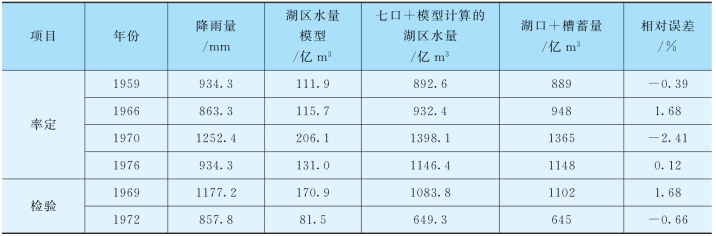
将实测的入湖七口控制站的径流量加上新安江模型计算的湖区径流量，与湖口水文站的实测水量加上江湖槽蓄量的结果进行比较，两者差值的百分比在-2.41%～1.68%之间，且有正有负，没有系统误差，说明采用新安江模型计算的湖区水量拟合精度良好。同时，根据实测资料分析，这6个典型年中，湖口及“五河七口”各水文站均无大的测验问题，不存在破圩、跑水、漏水等严重影响水量观测精度的情况，因此，可以认为在这6个典型年内水量是平衡的，根据这些年份的数据所率定并经过检验的参数是合理的。

3.利用新安江模型计算鄱阳湖区间径流

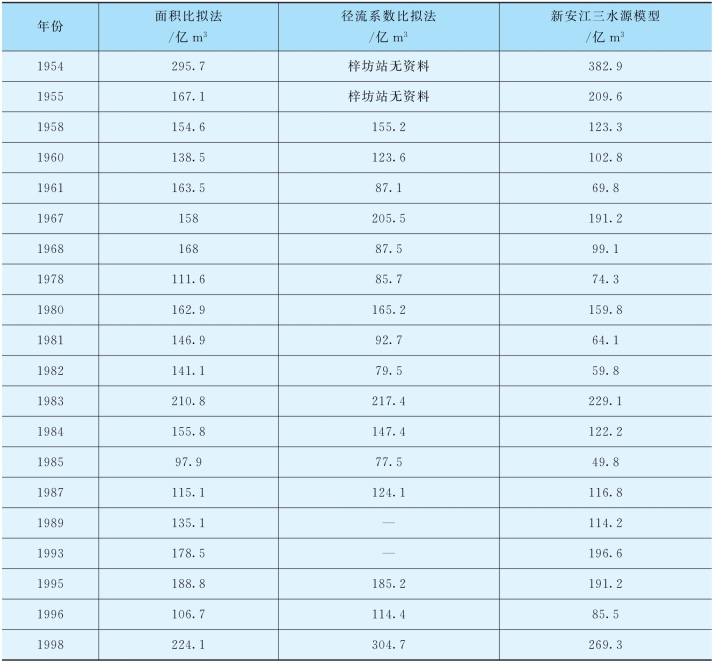
率定出参数后，就可根据实测降雨、蒸发资料，针对不平衡年份计算出鄱阳湖区间产水量。新安江三水源模型针对不平衡年份区间水量计算结果详见表4.3-7。

4.3.4.2 径流系数比拟法

径流系数比拟法是直接借用区间内用作水量平衡判断标准的水文站的径流系数分析成果，以分析不平衡年份的区间水量。由于整个鄱阳湖区间气候条件基本一致，陆面部分下垫面条件相似，采用径流系数比拟法具有一定的合理性。

表4.3-7　三种方法计算的区间水量结果比较表

分析区间水量时，将陆面和水面分开计算，陆面部分可直接借用梓坊站的径流系数，利用实测降雨量、蒸发量及湖区平均水位就可方便地分析出湖区水量。计算公式为(www.daowen.com)

式中：W区为湖区间水量；α为借用梓坊站的径流系数；P为降雨观测值；E为蒸发量；K为蒸散发能力折算系数；A陆面和A湖面分别为湖区的陆面和湖面面积。

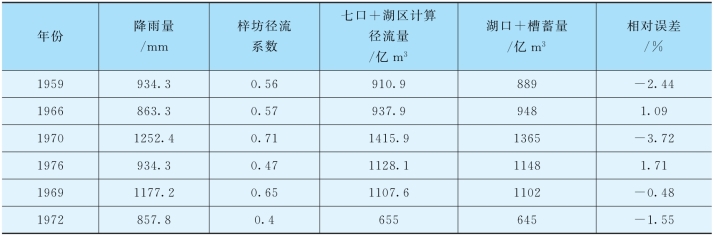
为检验径流系数比拟法计算结果的精度，选取整个湖泊区间水量相对平衡的年份，为具有可比性，同样选取新安江模型中率定及检验参数所采用的6个年份。根据径流系数比拟法计算的径流总量加上七口实测径流与湖口实测径流考虑槽蓄量后相比较的结果表见表4.3-8。

表4.3-8中结果显示，计算误差变化幅度在-3.72%～1.71%之间，有正有负，较为合理，有一定的精度。这表明，当湖区间有较好的实测资料时，采用径流系数比拟法计算区间不平衡年份的水量简单可行且有一定的精度。

表4.3-8　径流系数比拟法检验结果表

4.3.4.3 面积比拟法

“五河七口”控制站以上集水面积约为137147km2，鄱阳湖区间面积为25082km2，占五河控制面积的18.3%，假定区间降雨分布与“五河七口”所控制流域相一致，针对不平衡年份根据同期五河流量按此面积比例求出湖区区间的面积上的径流量，计算公式为

式中：W区和W七口分别为湖区区间水量和七口水量。

为检验面积比拟法计算结果的精度，同样选取新安江模型中率定及检验参数所采用的6个年份。根据面积比拟法计算的径流总量加上七口控制站实测径流与湖口实测径流考虑槽蓄量后相比较的结果见表4.3-9。

表4.3-9　面积比拟法检验成果表

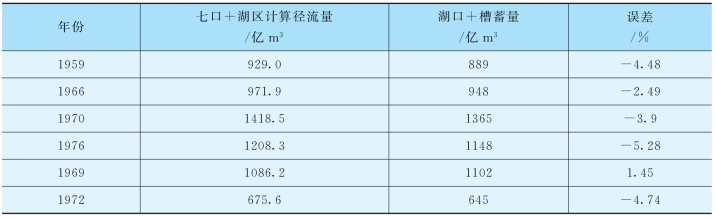
表4.3-9中结果显示，计算误差变化幅度在-5.28%～1.45%之间，除1969年为正误差外，其他均为负值，虽有一定的精度，但精度较差。这表明，采用面积比拟法计算湖区间水量精度较低。因此，只有在区间水量计算要求不高时，面积比拟法能够作为一种快速、简捷的方法来参考使用。

4.3.4.4 合理性分析

前面研究了鄱阳湖区水量平衡标准，通过参照标准即可以判别水量不平衡的现象，确定区间水量不平衡的年份为：1954年、1955年、1958年、1960年、1961年、1962年、1967年、1968年、1978年、1980年、1981年、1982年、1983年、1984年、1985年、1987年、1989年、1993年、1995年、1996年和1998年等21年。其中，1962年根据调查的跑水量已将其从不平衡年份中排除。有的年份如1973年、1975年和1977年跑水量很小，不影响定性分析。其他年份根据测验、断面冲淤变化、破圩、跑水、漏水调查及资料整编等方面进入深入分析，仍然无法定量分析出水量，只有采用合适的水文计算方法进行修正。根据新安江模型、径流系数比拟法和面积比拟法计算不平衡年份的区间水量结果见表4.3-7。

根据三种方法计算出不平衡年份区间水量，进而求出区间径流系数，并将其与梓坊站4—8月径流系数进行对比，见图4.3-6、图4.3-7和图4.3-8。

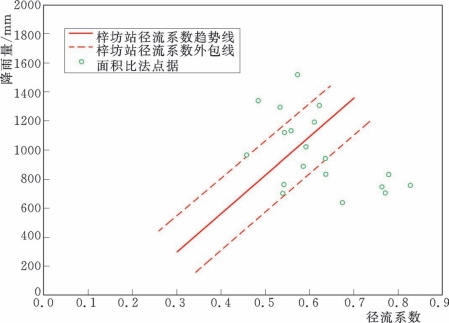
图4.3-6　鄱阳湖区间4—8月修正后径流系数分布图（面积比拟法）

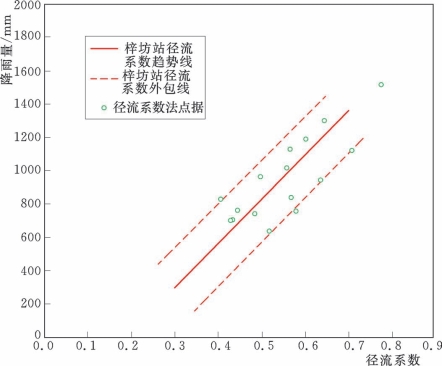
图4.3-7　鄱阳湖区间4—8月修正后径流系数分布图（径流系数比拟法）

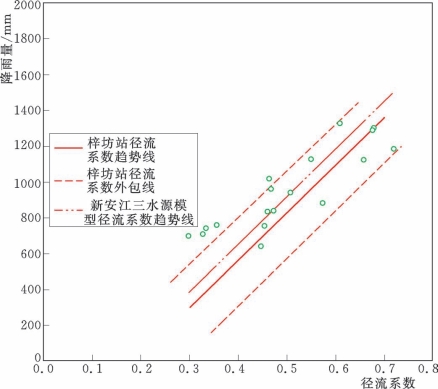
图4.3-8　鄱阳湖区间4—8月修正后径流系数分布图（新安江三水源模型）

图4.3-6显示，采用面积比拟法计算出来的径流系数只有约50%的点落在梓坊站径流系数外包线内，表明拟合精度较差。主要原因是其前提条件假定湖泊区间降雨与各支流的降雨是均匀分布且过程同步，但由于各支流流域面积非常大，达13.6万km2，区间面积也达2.6万km2左右，实际降雨过程较难满足这一条件，因此常导致较大偏差。但在4—8月主汛期内，常有大范围的降雨发生，与其假定相差不是非常大，故也有约50%的点达到较好效果。因此，采用面积比拟法，作为一种简捷的方法，只能得到供参考使用的初步结果。

图4.3-7是采用径流系数比拟法点绘而成。图中显示，所有点据都均匀地分布在梓坊趋势线左右，且落在其外包线内。径流系数比拟法点线配合良好的一个重要原因在于其计算结果是根据梓坊站本身的相应年份径流系数计算而成。采用此种方法计算区间水量的前提是代表站的水文特性与整个区间水文特性相一致。由于决定流域水文特性的因素众多，且代表性流域属山区性河流，而区间除含部分山区外，还由平原尾闾、圩垸区、湖泊水体等组成，二者虽有相似地方，但难以达到完全相一致。同时，采用此种方法计算时，对代表站测验精度也要求较高，如果该站也存在着测验问题，将直接导致计算成果的失真。因此采用径流比拟法计算区间水量受到一定的限制，总体而言，本方法是根据区间内的实测成果分析计算而来，在没有测验问题的情况下，计算简便且精度较高，仍不失为一种理想的计算方法。

图4.3-8是根据新安江三水源模型计算成果点绘而成。图中显示点据相对较为集中，且稳定在趋势线左右，同时，计算成果的趋势线比梓坊站趋势线偏左，这是因为鄱阳湖区比梓坊水文站多了一个面积较大的湖泊水面，所以，梓坊站的径流系数应该比湖区的径流系数略大，这说明本方法计算成果总体是合理可靠的。新安江三水源模型是一个分散性模型，针对湖区较为复杂的下垫面条件，它能对区间进行分块分单元计算，较为合理地由区间降雨模拟出区间逐日流量过程。同时，模型中考虑湖泊水位引起水、陆面比例变化对区间产水量的影响，也能满足突发事件情况下（如圩区汛期溃决时区间洪水逐日流量过程模拟要求），除计算略显复杂外，是一种良好的计算区间水量方法。