PCA-HUP模型基于贝叶斯理论，采用正态分位数转换技术，在正态空间中构建先验分布和似然函数，并应用主成分回归方法推求预报量的后验分布。从前文的应用情况可知，该模型不仅可以提供类似于确定性预报模型的定值预报结果（如均值、众数等），预报精度较高，还可以提供具有一定置信水平的区间预报结果，对预报的不确定性进行度量。由此可知，当一场洪水同时存在多个预报模型时，亦可以采用此法度量各个模型的不确定性：以不同模型的预报结果为输入，采用PCA-HUP模型分别实现概率预报，对比分析同一场洪水不同模型的预报区间，预报区间的离散度DI越大，不确定性越大，反之亦然。

本书选取淮河干流王家坝断面为研究对象，采用上述方法，分三种情景进行概率预报，对降低预报不确定性的方法进行了验证[108]。

情景一：以人工率定的新安江模型预报结果（简称人工率定）为输入，率定PCAHUP模型的相关参数，实现验证期洪水的概率预报。

情景二：以参数优化的新安江模型预报结果（简称参数优化）为输入，率定PCAHUP模型的相关参数，实现验证期洪水的概率预报。

情景三：以参数优化的新安江模型预报加以实时校正的结果（简称参数优化+实时校正）为输入，率定PCA-HUP模型的相关参数，实现验证期洪水的概率预报。

对比分析以上三种情景的预报区间离散度，具体流程见图5.4-1。

以前文所述1990—2013年间28场洪水为资料，其中20场用于率定相关参数，8场用于验证。为了更加直观地表现预报不确定性的变化，取Δt=6h，相关参数见表5.4-1，率定期洪水的预报区间对比见表5.4-2，离散度对比见图5.4-2。由表5.4-2可知，王家坝断面率定期22场洪水预报区间（本次仅以90%置信度为例，其他置信度亦然）的平均离散度分别为：情景一0.38，情景二0.36，情景三0.26，从情景一至情景三，离散度不断减小，说明预报的不确定性在不断降低；由图5.4-2也可以明显看出，情景一至情景三，每一场洪水的离散度均在减小。三种情景预报区间离散度的变化趋势验证了结论：新安江模型从人工率定到参数优化，再加以实时校正，是预报精度不断提高的过程，其预报不确定性在不断减小。

表5.4-1　PCA-HUP模型参数（王家坝）

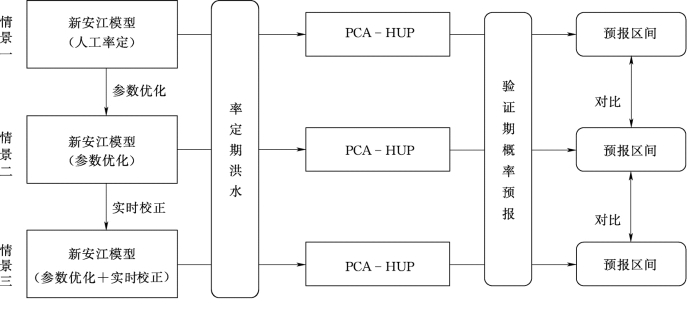
图5.4-1　降低预报不确定性的验证流程图

表5.4-2　PCA-HUP模型率定期洪水预报区间对比（王家坝，Δt=6h）

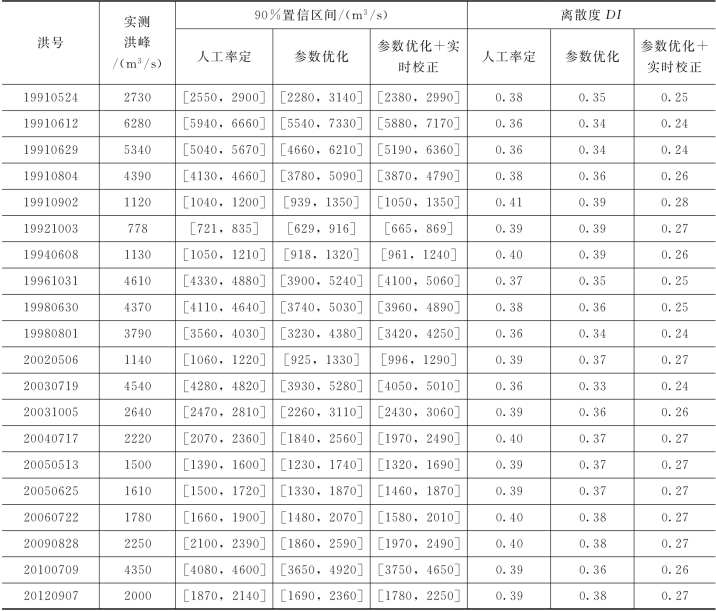
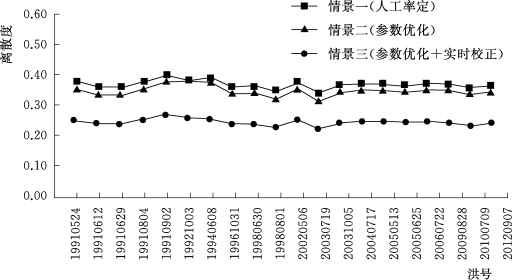
图5.4-2　预报区间离散度对比

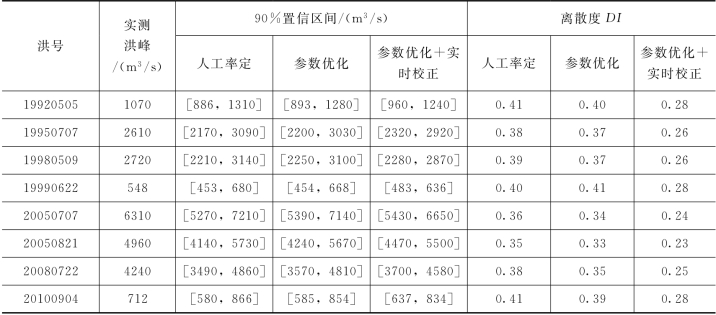
采用验证期8场洪水对上述结论再次进行验证，预报区间统计见表5.4-3，三种情景预报区间过程线见图5.4-3～图5.4-6。

表5.4-3　PCA-HUP模型验证期洪水预报区间对比（王家坝）

(www.daowen.com)

由表5.4-3和图5.4-3～图5.4-10这8场洪水预报区间过程线可知，由情景一到情景二再到情景三，预报区间宽度不断减小，离散度降低，表明预报不确定性在不断降低，与前文结论相符。综上所述，新安江模型从人工率定到参数优化，再加以实时校正，是预报精度不断提高的过程，其预报不确定性在不断减小。

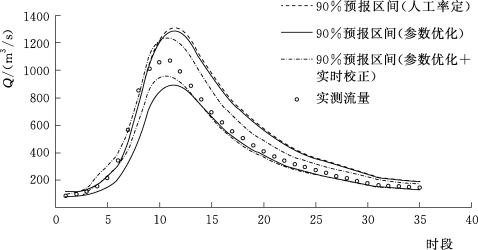
图5.4-3　19920505号洪水预报区间过程线（王家坝）

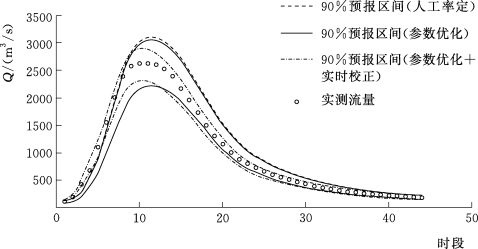
图5.4-4　19950707号洪水预报区间过程线（王家坝）

图5.4-5　19980509号洪水预报区间过程线（王家坝）

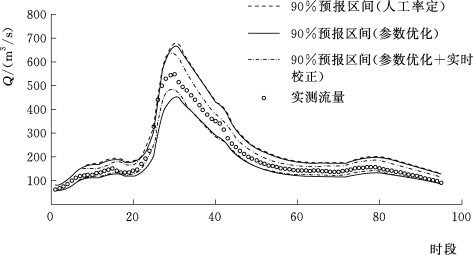
图5.4-6　19990622号洪水预报区间过程线（王家坝）

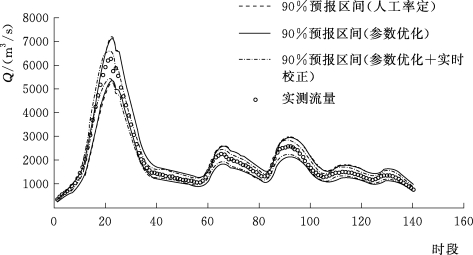
图5.4-7　20050707号洪水预报区间过程线（王家坝）

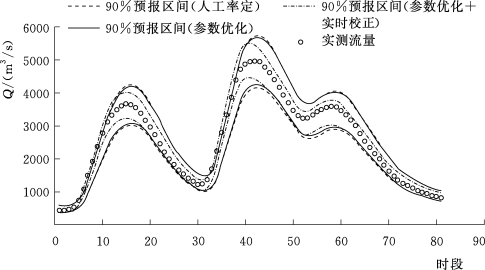
图5.4-8　20050821号洪水预报区间过程线（王家坝）

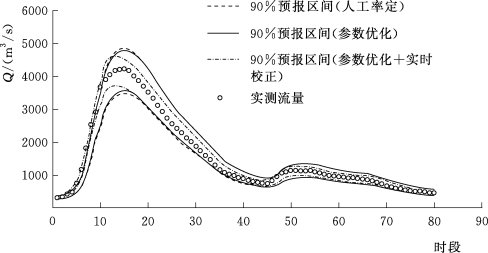
图5.4-9　20080722号洪水预报区间过程线（王家坝）

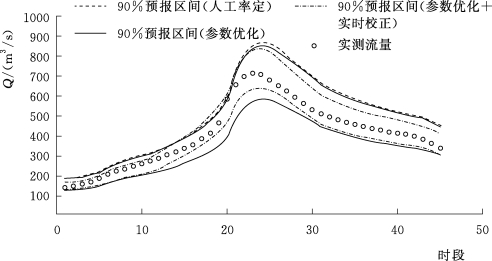
图5.4-10　20100904号洪水预报区间过程线（王家坝）