时间序列的自回归模型可以表达为

式中：t为当前时刻；X为时间序列（如流量、水位、相对误差等）；ξt为t时刻的系统残差；c1，c2，…，cp为常系数。

自回归模型假设t时刻变量Xt与t时刻之前变量X序列相关。根据t时刻之前变量X序列可以估计t时刻变量Xt，估计结果的好坏取决于回归系数。若已知时间序列为X1，X2，X3，…，Xm（m≥p），代入式（5.3-1）中，得到

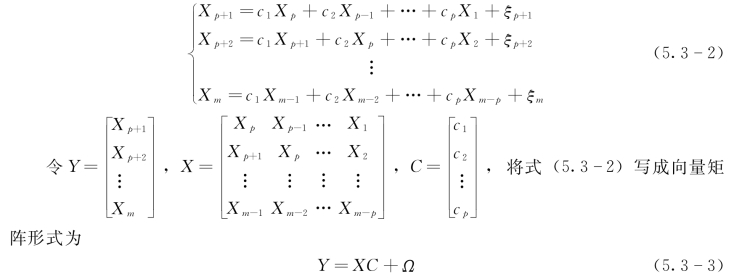
最小二乘原理指出，最佳参数C应满足残差平方和最小原则，则目标函数为

求J对C的偏微分，并令其等于0，则求得J趋于最小的估计值，有

普通最小二乘目标函数式（5.3-4）可以视为系统残差的等权结构，无法考虑新的洪水信息，为了加大新息在推导参数过程中的作用，人们又研制了衰减记忆最小二乘估计方法。该法是将最小二乘目标函数的等权结构改为加权结构，即将目标函数式（5.3-4）改写为

其中：ρ为加权因子，0＜ρ≤1。如果ρ=1，就是等权情况。

从式（5.3-6）可见，当m=i，也就是资料序列中i=1，…，m最新的一组数据所求出的残差ξm的权重ρm-m=1为最大，i逐个向前减少时，ξi的权重则从ρ，ρ2，ρ3，…，ρm-1逐个依次减小，由于减少呈指数方关系，ρ的大小对权重的衰减速度影响很大。(www.daowen.com)

根据国内外的经验，当ρ=0.6时，在最小二乘估计起作用的数据不超过9组；当ρ=0.9，则有30～40组数据起作用；在ρ=0.99可延长到400多组，而当ρ=0.9999时可记忆数据万组以上。由于在用加权和目标函数进行估计时，离当前时刻越久远的资料（m-i越大），计算的残差ξi越不起作用，这种“记忆”既往资料的能力是随时间逐步衰减的，因而得名。根据这一思路，可以推导出衰减记忆递推最小二乘的计算公式。

当从m组观测数据向（m+1）组递推的时候，按照式（5.3-6）的原理，最新观测数据的权重为l，过去的数据需要加乘权重ρ，使其权重衰减。

根据研究区数据特征，选用1阶自回归模型模拟预报误差的变化规律，将式（5.3-1）改写为

式中：t为时段；ξt为系统参数；A0、A1为回归参数；εt=为预报误差；Qc（t）、Qo（t）分别为t时段模型预报流量与实测流量。

根据式（5.3-7）可知，预报流量的校正式为

式中：Qc（*）、Qo（*）分别为模型预报流量与实测流量；t为时段；为模型校正流量。

以王家坝断面为例，采用最小二乘法对式（5.3-7）中参数进行估计，以1990—2013年间28场洪水数据为资料，预报误差1阶自回归拟合见图5.3-3。

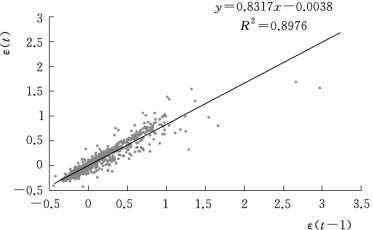
图5.3-3　预报误差1阶自回归拟合

自回归模型的初始参数为A1=0.8317，A0=-0.0038，线性相关系数R=0.95，线性相关程度较高。