原则上，任何模型的任一参数都可通过参数率定方法确定。然而，模型参数的率定是一个十分复杂和困难的问题。流域水文模型除了模型的结构要合理外，模型参数率定也是一个十分重要的环节。新安江模型的参数大多具有明确的物理意义，因此，它们的参数值原则上可根据其物理意义直接定量。但由于缺乏降雨径流形成过程中各要素的实测与试验过程。故在实际应用中只能依据出口断面的实测流量过程，用系统识别的方法推求，由于参数多，信息量少，就会产生参数的相关性、不稳定性和不唯一性的问题[90，91]。下面就新安江模型参数的敏感性问题、参数的相关性问题、参数的人工优化和自动优化做一些探讨。

（1）参数的敏感性分析。所谓参数的敏感性是指将待考察的参数增加或减少一个或适当的数量，再进行模拟计算，观察它对模拟结果和目标函数变化的影响程度，这也叫参数的灵敏度；参数改变后的模拟结果与参数改变前的模拟结果改变越大，则说明此参数越敏感；反之，当参数改变后的模拟结果与参数改变前的模拟结果基本不变，则说明此参数反应迟钝、不敏感[92，93]。敏感性参数，其数量稍有变化对输出的影响就很大；反之迟钝的参数，对输出影响不大；有的参数在湿润季节敏感，在干旱季节不敏感，而另外的参数则反之；有的参数在高水时敏感，低水时不敏感，而另外的参数则反之。对敏感性的参数应仔细分析，认真优选；对不敏感的参数分析可粗略一些或根据一般经验固定下来，不参加优选[94-96]。

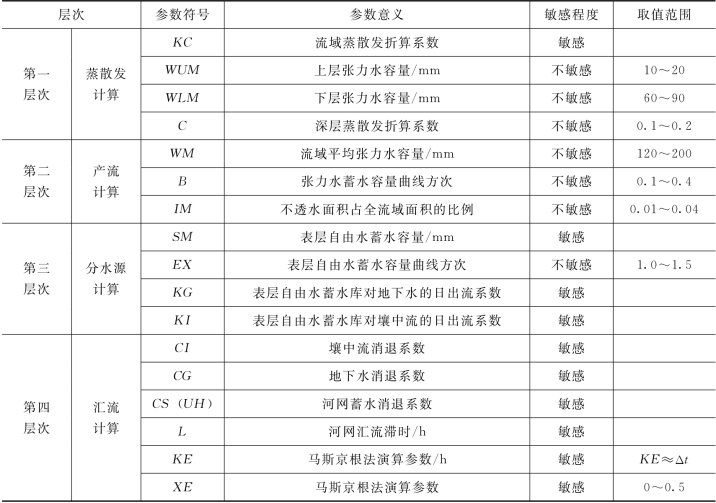
新安江模型参数可分为蒸散发计算、产流计算、分水源计算和汇流计算四类，各层次参数见表5.2-1，表中提及的各参数取值，仅供参考。在应用中，应根据特定流域的具体情况来确定。

表5.2-1　新安江模型各层次参数表

（2）参数的相关性分析。模型参数的相关性分析历来是模型研制者关注的重点问题，模型中只要有相关程度较高的参数存在，其解就不稳定，也不唯一，为了解决参数的相关性问题，可按新安江模型的层次结构率定参数，每个层次分别采用不同目标函数的优化方法。

实际应用中发现，新安江模型有些参数之间的不独立性既存在于层次之内，也存在与层次之间。

1）层次之间参数的相关性分析。

a.第一、第二层次之间的参数。当第二层次中参数B有变化时，对总径流量R的计算结果会产生一定的影响。因此就会影响总的水量平衡，也就影响了第一层次参数的调试结果，结果表明：这种作用很小，因为它们只在局部蓄满产流时起作用，当全流域蓄满时就没有作用了。参数B可根据次洪的降雨径流关系求出，因此与第三层次参数无关，对参数B分析结果见表5.2-2。

表5.2-2　参数B敏感性分析

由表5.2-2可见，随着参数B值的增大，计算的年径流量有增大的趋势，但影响较小，对水源划分的影响更小。WM不影响蒸散发计算，因此与第一层次参数无关。但WM与B有关，因此，对产流产生一些间接影响。天然流域IM很小，影响不大，但都市化地区IM较大，对产流有一定的影响。WM只与B有关，与第三层次的参数也无关，IM也与其他参数无关。(www.daowen.com)

b.第二、第三层次之间的参数。由于产流计算采用蓄满产流，在分水源以前，总径流量R已经计算好，所以第三层次参数完全不影响第二层次参数。

c.第三、第四层次之间的参数。在分水源计算结束后，所求得的是河网总入流。汇流计算只处理河网汇流问题，与水源划分无关。所以第三、第四层次之间的参数在性质上是完全独立的。但在优化参数时，都是根据流域出口断面的流量过程线，因此在定量上有一定的相关性。但流量过程线与这两个层次之间参数的关系，可以通过流量过程线的分段处理来解决。在高水部分流量基本上是由地面径流和壤中流组成，主要调控参数SM、EX、KG+KI、UH（CS、L）；退水段尾部流量基本上是由地下水组成的，主要调控参数KG/KI、CG。因此，若分段采用不同的目标函数，可以克服某些参数之间的相互不独立性问题。

2）同一层次中参数的相关性分析。

a.第一层次中的参数。在第一层次中，若加大WUM、WLM、C的值，计算蒸散发量E值就会增加。因此，为了控制数量平衡，调试时就会减小KC的值。由于WUM与WLM都有一定的变化范围，所以这种影响是有限的。对WUM与WLM的分析结果见表5.2-3，从表中可以看出，随着WUM的增大和WLM的减小，年径流量有逐渐减小的趋势，但WUM与WLM对年径流影响不大。

表5.2-3　WUM与WLM的敏感性分析

深层蒸散发扩散系数C值只对干旱季节起作用，由于湿润地区很少用到深层蒸散发计算，所以一般情况下它是不敏感的，但对于半湿润地区，它则是重要的。

b.在第二层次中的参数。在第二层次中，如果流域蓄水容量-面积分布曲线保持不变，则WM值越大，B值越小，两者并不是独立的，它们共同确定了流域蓄水容量-面积分布曲线。在第一、第二层次之间参数分析中已论述，WM不敏感，它只代表蓄满的标准，并不影响蒸散发计算。WM有一个约束条件，就是模型计算中W0不能出现负值，若出现负值，WM要酌情加大。

c.第三层次中的参数。在新安江模型中，第三层次参数是敏感和重要的，参数相互之间的关系也相对比较复杂，需要认真分析。SM与EX之间是不独立的，它们共同确定了自由水蓄水容量-面积分布曲线。存在的问题和WM与B之间存在问题大致相同。但WM与B之间关系可以根据降雨径流相关图推求出，而SM与EX之间的关系则没有类似的途径可以解决，只能采用优化检验的方法分析。方法是先根据经验调试好全部参数，然后将其他参数固定不变，只调试SM与EX，确定最优解的范围。据分析研究，EX值大体上反映了流域自由水分布的不均匀程度。其值的最优范围在1.0～1.5左右，变幅不大，因此可以将EX定为1.5，不参加优选。

SM与KG+KI间存在相关关系。若KG+KI和EX固定，SM就决定了地面径流的多少，KG/KI就决定了壤中流和地下径流的比例。当SM增大时，RS要减小；若同时减小KG+KI，则RS可以保持不变；若KG/KI也不变，则RI与RG也保持不变。这三个参数之间是不独立的，这种不独立是由线型水库结构所造成的，采用结构性约束KG+KI=0.7来解决。这等于把参数减为两个，SM与KG的独立性增强了，可优化得出唯一解，只有这种解才存在各流域之间的可比性，找出区域性的规律。分析方法是先根据经验调试好所有参数，然后将其他参数固定不变，只调试SM与KG/KI，确定最优解范围。

由上述分析可知，分水源层次参数的独立性问题特别复杂，必须要结构性约束才能解决，如不加约束，则各种模型的分水源参数的最优解可能有多种组合。

d.第四层次中的参数。在汇流层次中，CI的作用是弥补KG+KI=0.7的不足。它取决于退水段退水流量的快慢，与其他因素无关，因此相对比较独立，他对整个过程的影响远不及SM与KG/KI明显。CG取决于地下径流的退水快慢，也相对比较独立，用枯季径流的资料很容易确定。UH（或L、CS）决定于流量过程线中高水部分，因此与第三层次参数之间是比较独立的。L与CS的功能不同，前者处理平移，后者处理坦化，相互间是很独立的。UH（或L、CS）与KE、XE之间具有相关性。解决的方法是：若单元面积汇流快一些，则河网汇流就可以慢一些，反之亦然，使它们相互间有一定的补偿作用。