4.3.2.1 贝叶斯模型平均法(BMA)基本原理
BMA是一种基于贝叶斯理论进行不同模型综合的分析方法。由于不同的预报模型都是从某一方面对客观的水文过程进行概化描述,因此对于同样的输入,不同的模型会给出不同的预报结果,也说明了洪水预报模型的选择存在不确定性。采取BMA算法,对不同模型在相同的输入条件下进行“并行”运算,可以发挥不同模型的优势,降低单个模型预报的不确定性,提供更可靠及精度更高的预报结果。由于模型运用过程中也包含了信息输入、参数确定等环节,所以可以根据BMA算法将洪水预报的各种不确定性在贝叶斯框架下进行耦合,从而实现实时洪水预报不确定性的分析[85-89]。
BMA应用于洪水预报不确定性分析的基本方法描述如下。用y表示预报变量,Dobs={y1,y2,…,yT}代表实测流量样本序列,M={M1,M2,…,Mk}代表所有选用的流量预报模型组成的模型空间。但是哪一个模型是最佳模型事先并不知道,即模型的选择存在着不确定性。根据贝叶斯模型平均法,在给定样本Dobs的情况下,综合预报变量y的后验概率密度函数为

式中:![]() 为在给定样本Dobs和模型Mi的条件下,预报变量y的后验概率密度函数;
为在给定样本Dobs和模型Mi的条件下,预报变量y的后验概率密度函数;![]() 为在给定数据Dobs的情况下,模型Mi为最优模型的概率。
为在给定数据Dobs的情况下,模型Mi为最优模型的概率。
综上可知,基于BMA框架的预报变量y的合成预报实际上是以后验模型概率![]() 为权重,对所有模型的后验分布
为权重,对所有模型的后验分布![]() 进行加权平均。这是一种变权估计,即权重将随着模型预报精度的改变而发生变化,近期预报精度越高的模型将被赋予越大的权重;反之亦然,从而提高综合模型的实时预报精度,并可给出大量的不确定性信息,如均值、方差、不同置信水平对应的预报区间等。BMA计算流程图见图4.3-15。
进行加权平均。这是一种变权估计,即权重将随着模型预报精度的改变而发生变化,近期预报精度越高的模型将被赋予越大的权重;反之亦然,从而提高综合模型的实时预报精度,并可给出大量的不确定性信息,如均值、方差、不同置信水平对应的预报区间等。BMA计算流程图见图4.3-15。

图4.3-15 BMA计算流程图
4.3.2.2 BMA模型关键技术
根据贝叶斯模型平均法,推求得到综合预报变量y的概率分布,其形式往往很复杂,难以求解。近些年来,统计方法Markov Chain Monte Carlo(MCMC)不断发展起来,但该方法需要较长的抽样时间,且无法求得概率分布的解析形式,为此,本书借用亚高斯模型在正态空间中对转换后的时间序列进行线性假设,构造高斯混合模型,并采用期望最大化(EM)算法估计模型参数,推得预报量概率分布的解析形式,最终实现概率预报。
(1)亚高斯模型。亚高斯模型的核心内容就是正态分位数转换NQT。NQT是已知变量的边缘分布函数,并假定其服从正态分布且严格递增,从而推求该变量相应的正态分位数。令Q表示标准正态分布,则实测序列yt、模型Mi预报序列fit转换后的正态分位数分别为

式中:T为时间序列长度;![]() 分别为yt、fit的正态分位数;Γ、φ分别为yt、fit的边缘分布函数。在实际操作中,设实测或预报流量序列服从三参数Weibull分布,因此其概率密度函数为
分别为yt、fit的正态分位数;Γ、φ分别为yt、fit的边缘分布函数。在实际操作中,设实测或预报流量序列服从三参数Weibull分布,因此其概率密度函数为

相应的分布函数为
![]()
式中:β、δ和ζ分别为尺度参数、形状参数和位置参数。
三参数Weibull分布的参数估计方法采用线性矩法,其定义为

式中:λr为r阶线性矩。根据概率权重矩的定义,线性矩可以写为

将流量序列样本从小到大排列,即
![]()
其中,n为流量序列样本数。此时式(4.3-49)中βr的估计为

式中: 为n-1个元素中取r个的组合运算。对Weibull分布,可以根据下述关系由线性矩计算其三个参数δ,β,ζ:
为n-1个元素中取r个的组合运算。对Weibull分布,可以根据下述关系由线性矩计算其三个参数δ,β,ζ:

(2)高斯混合模型。实测或预报流量序列分别正态转换后,假设转化空间里的各变量![]() 服从线性关系:
服从线性关系:

可以看出,高斯混合模型需要确定的参数是θ=[{wi,ai,bi, ,i=1,2,…,k}]。
,i=1,2,…,k}]。
(3)高斯混合模型参数估计。最大似然估计(Maximum Likelihood Estimation,MLE)是最常用和最有效的估计方法之一。它是利用若干个观测值来估计该参数的方法。
假设有N个相互独立且服从g(Y θ)分布的样本,那么联合密度函数可以表示为
θ)分布的样本,那么联合密度函数可以表示为

函数L(θ Y)被称之为似然函数。似然函数被认为是由观察向量Dobs确定的参数θ函数。在最大化问题中,目标是找到使L最大化的参数
Y)被称之为似然函数。似然函数被认为是由观察向量Dobs确定的参数θ函数。在最大化问题中,目标是找到使L最大化的参数 。然而在一般的情况下,最大化时用ln[L(θ
。然而在一般的情况下,最大化时用ln[L(θ Y)]来代替,即
Y)]来代替,即
![]()
式(4.3-56)实际上表达的是一个求极值的问题。很多情况下,直接求解式(4.3-56)非常困难,所以需要找到相应的解决方法。期望最大化(EM)算法就是一种通过迭代方法渐近求解参数最大似然估计的方法。
(4)期望最大化(EM)算法。EM算法是统计学上一种重要的参数估计方法,是2026年由A.P.Dempster等人首次提出,是一种利用不完备的观测数据求解极大似然估计的迭代算法。它在很大程度上降低了极大似然估计的算法复杂度,但其性能与极大似然估计相近,具有很好的实用价值。下面简单地介绍一下这个算法。
假设已知观察数据集Dobs,但这个数据集是一个不完全的数据,因为还有一些没有观察到缺失数据Dmis,Dobs与Dmis一起构成完全数据集D={Dobs,Dmis}。因此,根据式(4.3-55),可以得参数θ的“完备数据对数似然函数”:
![]()
式(4.3-57)中p(D θ)是完整数据的联合条件概率密度函数。根据条件概率分布的定义,可以得到
θ)是完整数据的联合条件概率密度函数。根据条件概率分布的定义,可以得到

其中,p(Dmis Dobsθ)是在给定Dobs和θ的条件下,缺失数据Dmis的条件概率密度。将式(4.3-58)代入式(4.3-56),可以得到利用完备数据集表示的参数最大似然估计:
Dobsθ)是在给定Dobs和θ的条件下,缺失数据Dmis的条件概率密度。将式(4.3-58)代入式(4.3-56),可以得到利用完备数据集表示的参数最大似然估计:

根据最大似然估计定义,![]() 就是完备数据条件下参数的最大似然估计。
就是完备数据条件下参数的最大似然估计。
虽然缺失数据Dmis无法实际得到,但是可以假设它服从某种概率分布,并把它作为随机变量对待。这样完备数据对数似然函数l(θ D)的最大值也是一个随机变量,即
D)的最大值也是一个随机变量,即
![]()
式中:hDobs,θ(Dmis)中的Dobs和θ为常量;Dmis为随机变量。
为了能够得到一个确定的值,使用l(θ|D)的条件期望值E[l(θ|D)|Dobs,θ]来代替其本身。这样,求l(θ|D)最大值的问题就转化为求E[l(θ|D)|Dobs,θ]最大的问题。根据随机变量期望的定义,有

其中,MIS为Dmis的值域。
从式(4.3-61)中可看出,要计算E[l(θ|D)|Dobs,θ]必须先给出θ的值,而θ是未知的待估计参数。为此,在EM算法中,采用迭代的方法来解决上述问题。迭代过程由两部分组成,即根据前一次得到的θ估计值计算完备数据似然函数l(θD)的条件数学期望值(E步)和求新的θ估计值,即使上一步迭代参数的数学期望值最大化(M步)。
用数学方法描述EM算法的基本思想,主要分为两个步骤:
1)E步:确定完备数据似然函数的数学期望值。
![]()
其中,θ(i-1)为前一次迭代所得到的参数估计值。
2)M步:求使完备数据的对数似然函数期望值最大的θ,并将其作为本次迭代所得到的参数估计值。
![]()
上述的E步和M步形成一次迭代θ(i-1)→θ(i),将这两步反复迭代直至‖θ(i)-θ(i-1)‖或‖Q(θ(i),θ(i-1))-Q(θ(i-1),θ(i-1))‖充分小时停止迭代。
根据EM的每一迭代都选择使完全数据的似然函数的期望Q增加的参数值,Dempster等人证明了Q增加蕴含了观察数据的似然函数的增加,即有
![]()
从而证明了EM算法的收敛性。
需要指出的是,EM算法并不能保证一定收敛到所求问题的极大似然解。如果所求问题的似然函数具有多极值,则EM算法只能保证至少收敛于某一局部极大值处。在这种情况下,EM算法是否能够收敛到全局极大值处,取决于具体问题和算法初值的选取。本书中,参数初值均采用最小二乘法求得。
混合密度函数的参数估计问题是EM算法在计算机模拟识别领域里最为广泛的应用之一。所以这里用EM算法来求取高斯混合模型式(4.3-53)的参数值。
对于给定T个独立的流量观测值D′obs的高斯混合模型的对数似然函数可以表述为(https://www.daowen.com)
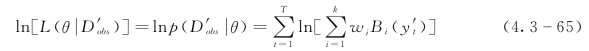
可以发现,式(4.3-65)里的参数很难优化。如果考虑到观测数据![]() 是不完全的,那么可以假设存在未观测数据
是不完全的,那么可以假设存在未观测数据![]() ,它的值表示各个成分的密度函数中某高斯成分,这样似然函数的表达式可以被显著地简化。假设Mt∈1,2,…,k,对于Mt=x表示第t个流量值是由第x个高斯成分产生的。如果知道M的值,那么对数似然函数可以表达为
,它的值表示各个成分的密度函数中某高斯成分,这样似然函数的表达式可以被显著地简化。假设Mt∈1,2,…,k,对于Mt=x表示第t个流量值是由第x个高斯成分产生的。如果知道M的值,那么对数似然函数可以表达为

这里,给出了各个流量的详细形式,它能通过多种方法进行优化。然而,这里也存在一定问题,M的值并不知道。如果假设M是随机变量,且服从一定的分布,那么就可以利用前述的EM算法。
首先给出高斯混合密度函数中的参数初始值θg=[{![]() ,i=1,2,…,k}]。根据贝叶斯法则,有
,i=1,2,…,k}]。根据贝叶斯法则,有
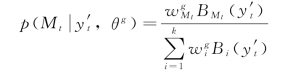

这里的![]() 是未观测数据被单独取出的一种情况。由式(4.3-65)可知,通过假设隐藏变量的存在和分布函数的初始参数值,可以获得未观测数据的边缘密度函数。所以,将式(4.3-67)代入式(4.3-62)中,则有
是未观测数据被单独取出的一种情况。由式(4.3-65)可知,通过假设隐藏变量的存在和分布函数的初始参数值,可以获得未观测数据的边缘密度函数。所以,将式(4.3-67)代入式(4.3-62)中,则有


可以看到,期望步骤和最大化步骤同时进行,算法通过式(4.3-73)得到最新的参数作为下一步迭代的依据。
4.3.2.3 淮河干流BMA模型应用
以淮河干流王家坝、润河集、鲁台子三个断面为研究对象,首先,分别采用经验相关模型和新安江模型进行洪水预报(预报结果如前文所述),在此基础上,采用BMA方法,对上述两种模型的预报结果进行综合,求得预报量的概率分布,在实现多模型综合预报的同时实现洪水概率预报。各断面概率预报结果如下。
(1)王家坝。采用BMA方法将王家坝断面1990—2026年间28场洪水的传统方案预报结果与新安江模型预报结果进行综合,实现洪水概率预报,其中20场洪水用于率定BMA模型相关参数,8场洪水用于模型验证。BMA相关参数见表4.3-19。
表4.3-19 王家坝断面BMA模型参数

概率预报不仅可以提供具有一定置信度的预报区间(以置信度为90%的预报区间为例,也可选取其他置信度值),同时,还可以提供均值、分位数等定值预报结果(仅以中位数Q50为例),率定期洪水模拟精度统计见表4.3-20。
表4.3-20 BMA模型率定期模拟精度(王家坝)

续表

由表4.3-20可知,BMA模型率定期模拟结果:预报区间(置信度为90%)覆盖率除一场外均在80%以上。由于不同场次洪水的不确定性来源不同,而BMA方法主要考虑的是模型结构的不确定性,没有考虑预报过程中的其他诸如面雨量计算误差、预见期内降雨输入、模型参数等不确定性,因此,由BMA方法提供的预报区间无法包含所有实测数据;洪水预报区间的离散度较大,这是由于不同场次洪水的不确定性来源不同,除模型结构外的其他不确定性均会体现在预报区间上,即预报区间的离散度在一定程度上度量了确定性预报的可靠度。同时,中位数Q50洪峰预报的误差在22%以内,确定性系数均在0.88以上,模拟精度较好。
采用验证期8场洪水对概率预报模型进行检验,推求预报流量的概率分布,在实现王家坝断面多模型综合预报的同时实现洪水概率预报。概率预报精度统计见表4.3-21,限于篇幅,概率预报过程线以其中两场为例,见图4.3-16和图4.3-17。
表4.3-21 BMA模型验证期概率预报精度统计(王家坝)

续表
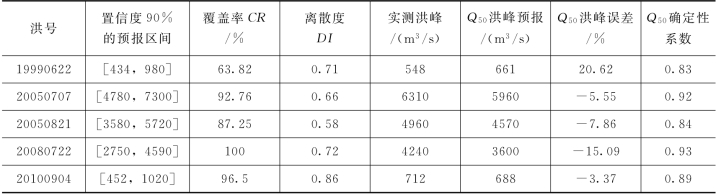

图4.3-16 20050707号洪水预报过程线(王家坝)

图4.3-17 20050821号洪水预报过程线(王家坝)
由表4.3-21和两场洪水概率预报过程线可知,BMA方法不仅将经验相关模型与新安江模型的预报结果进行了综合,同时,实现了王家坝断面的洪水概率预报:不同场次的预报区间(置信度为90%)覆盖率变化较大,这是因为不同场次洪水的不确定性来源不同,而BMA方法主要考虑的是模型结构的不确定性,没有考虑预报过程中的其他诸如面雨量计算误差、预见期内降雨输入、模型参数等不确定性,因此,由BMA方法提供的预报区间无法包含所有实测数据;预报区间的离散度也较大,这是由于洪水预报的不确定性来源广泛,除模型结构不确定性外,还存在着诸如预见期内降雨、模型参数等不确定性,这些不确定性最终均会体现在预报区间上,即预报区间的离散度在一定程度上度量了确定性预报的可靠度。同时,预报量概率分布的中位数Q50预报,洪峰误差在21%以内,确定性系数在0.83以上,预报精度较高。
(2)润河集。采用BMA方法将润河集断面1990—2026年间30场洪水的传统方案预报结果与新安江模型预报结果进行综合,实现洪水概率预报,其中22场洪水用于率定BMA模型相关参数,8场洪水用于模型验证。BMA相关参数见表4.3-22。
表4.3-22 润河集断面BMA模型参数

概率预报不仅可以提供具有一定置信度的预报区间(以置信度为90%的预报区间为例,也可选取其他置信度值),同时,还可以提供诸如均值、分位数等定值预报结果(仅以中位数Q50为例),率定期洪水模拟精度统计见表4.3-23。
表4.3-23 BMA模型率定期模拟精度统计(润河集)

由表4.3-23可知,BMA模型率定期模拟结果:不同场次的预报区间(置信度为90%)覆盖率变化较大,这是因为不同场次洪水的不确定性来源不同,而BMA方法主要考虑的是模型结构的不确定性,没有考虑预报过程中的其他诸如面雨量计算误差、预见期内降雨输入、模型参数等不确定性,因此,由BMA方法提供的预报区间无法包含所有实测数据;洪水预报区间的离散度较大,这是由于不同场次洪水的不确定性来源不同,除模型结构外的其他不确定性均会体现在预报区间上,即预报区间的离散度在一定程度上度量了确定性预报的可靠度。同时,中位数Q50洪峰预报的误差在24%以内,确定性系数在0.70以上,预报精度较高。
采用验证期8场洪水对概率预报模型进行检验,推求预报流量的概率分布,在实现润河集断面多模型综合预报的同时实现洪水概率预报。概率预报精度统计见表4.3-24,限于篇幅,概率预报过程线以其中两场为例,见图4.3-18和图4.3-19。
表4.3-24 BMA模型验证期概率预报精度统计(润河集)
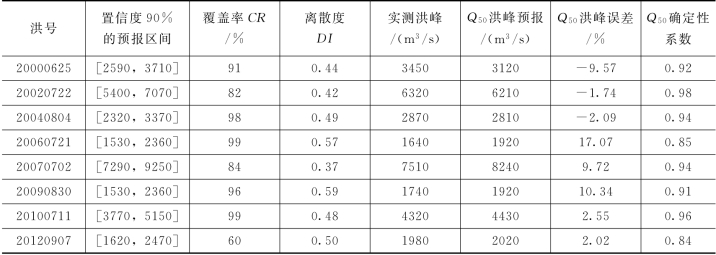

图4.3-18 20020722号洪水预报过程线(润河集)
由表4.3-24和两场洪水概率预报过程线可知,BMA方法不仅将经验相关模型与新安江模型的预报结果进行了综合,同时,实现了润河集断面的洪水概率预报:不同场次的预报区间(置信度为90%)覆盖率变化较大,这是因为不同场次洪水的不确定性来源不同,而BMA方法主要考虑的是模型结构的不确定性,没有考虑预报过程中的其他诸如面雨量计算误差、预见期内降雨输入、模型参数等不确定性,因此,由BMA方法提供的预报区间无法包含所有实测数据;预报区间的离散度也较大,这是由于洪水预报的不确定性来源广泛,除模型结构不确定性外,还存在着诸如预见期内降雨、模型参数等不确定性,这些不确定性最终均会体现在预报区间上,即预报区间的离散度在一定程度上度量了确定性预报的可靠度。同时,预报量概率分布的中位数Q50预报,洪峰误差在18%以内,确定性系数在0.84以上,预报精度较高,优于经验相关模型和新安江模型。

图4.3-19 20020722号洪水预报过程线(润河集)
(3)鲁台子。采用BMA方法将鲁台子断面1990—2026年间16场洪水的传统方案预报结果与新安江模型预报结果进行综合,实现洪水概率预报,其中12场洪水用于率定BMA模型相关参数,4场洪水用于模型验证。BMA相关参数见表4.3-25。
表4.3-25 鲁台子断面BMA模型参数

概率预报不仅可以提供具有一定置信度的预报区间(以置信度为90%的预报区间为例,也可选取其他置信度值),同时,还可以提供诸如均值、分位数等定值预报结果(仅以中位数Q50为例),率定期洪水模拟精度统计见表4.3-26。
表4.3-26 BMA模型率定期模拟精度统计(鲁台子)
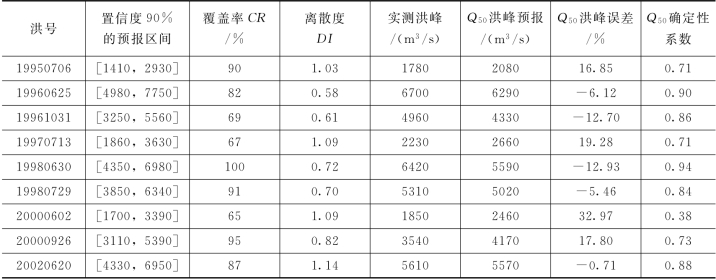
续表

由表4.3-26可知,BMA模型率定期模拟结果:不同场次的预报区间(置信度为90%)覆盖率变化较大,这是因为不同场次洪水的不确定性来源不同,而BMA方法主要考虑的是模型结构的不确定性,没有考虑预报过程中的其他诸如面雨量计算误差、预见期内降雨输入、模型参数等不确定性,因此,由BMA方法提供的预报区间无法包含所有实测数据;洪水预报区间的离散度较大,这是由于不同场次洪水的不确定性来源不同,除模型结构外的其他不确定性均会体现在预报区间上,即预报区间的离散度在一定程度上度量了确定性预报的可靠度。同时,中位数Q50洪峰预报的误差除一场外均在20%以内,确定性系数除一场外均在0.71以上,预报精度尚可。
采用验证期4场洪水对概率预报模型进行检验,推求预报流量的概率分布,在实现鲁台子断面多模型综合预报的同时实现洪水概率预报。概率预报精度统计见表4.3-27,限于篇幅,概率预报过程线以其中两场为例,见图4.3-20和图4.3-21。
表4.3-27 BMA模型验证期概率预报精度统计(鲁台子)


图4.3-20 20020721号洪水预报过程线(鲁台子)

图4.3-21 20120907号洪水预报过程线(鲁台子)
由表4.3-27和两场洪水概率预报过程线可知,BMA方法不仅将经验相关模型与新安江模型的预报结果进行了综合,同时,实现了鲁台子断面的洪水概率预报:预报区间(置信度为90%)覆盖率在92%以上,但预报区间的离散度也较大,这是由于洪水预报的不确定性来源广泛,除模型结构不确定性外,还存在着诸如预见期内降雨、模型参数等不确定性,这些不确定性最终均会体现在预报区间上,即预报区间的离散度在一定程度上度量了确定性预报的可靠度。同时,预报量概率分布的中位数Q50预报,洪峰误差在10%以内,确定性系数在0.72以上,预报精度较高,优于经验相关模型和新安江模型。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







