4.3.1.1　HUP基本原理

水文不确定性处理器（Hydrologic Uncertainty Processor，HUP）是贝叶斯概率预报系统（BFS）的主要组成部分，用以分析除降雨之外的其他所有不确定性。其特点是，不需要直接处理预报模型的结构与参数，而是从预报结果入手，分析其与实测水文过程的误差，再利用贝叶斯公式估计预报变量的概率分布，从而实现水文模型预报结果的不确定性分析及概率预报[81，82]。其工作流程见图4.3-2。

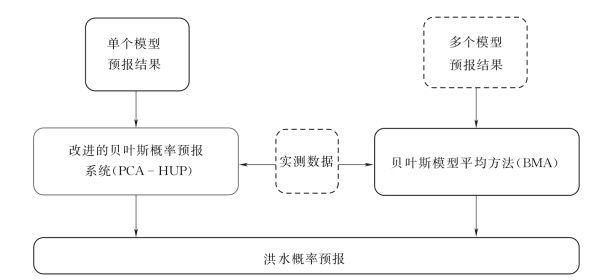
图4.3-1　基于预报误差分析的洪水概率预报研究思路

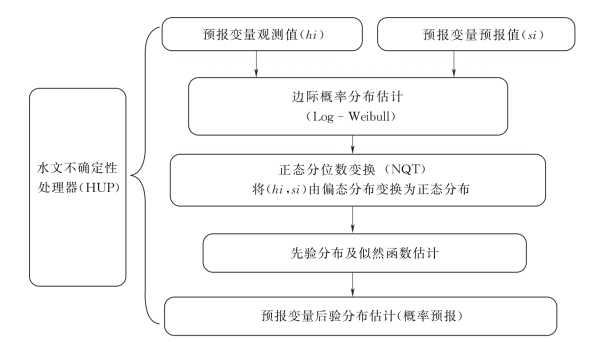
图4.3-2　水文不确定性处理器工作流程示意图

（1）边际分布。选用汛期的洪水流量资料{h0}求解H0的边缘分布函数Γ。对于边缘分布函数Γ，可以采用任意的分布，可以是参数的也可以是非参数的。常用的参数分布有：Gamma分布、Log-Pearson分布、Log-Normal分布、Log-Weibull分布、Weibull分布、Kappa分布等。在实际工作中，针对不同流域、不同季节，可以选用不同的分布，选用的标准是使得假定分布与经验分布的标准差最小。Krzysztofowicz通过研究比较，建议采用Log-Weibull（对数威布尔）分布，其密度函数与分布函数分别为

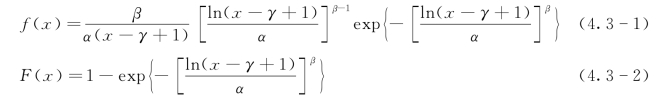
其中，α、β和γ是待定的三个参数。

选用汛期的洪水流量资料{h0}，利用H0的经验点据进行参数估计。为减小计算量、简化计算程序，在实际操作过程中先对流量资料进行对数处理，然后用矩法对三参数Weibull分布进行参数估计。三参数Weibull分布的密度函数与分布函数分别为

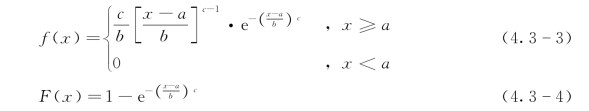
式中：a、b、c为三参数Weibull分布的三个待定参数，其意义分别为a为位置参数；b为尺度参数；而c为形状参数。

用矩法估计三个参数要用到前三阶矩。

先利用样本资料计算出偏态系数Cs，然后由式（4.3-8）反解出c，那么可由式（4.3-9）和式（4.3-10）分别求出d和e。最后可求出参数b和a。

（2）亚高斯模型。亚高斯模型（Meta-Gaussian Model）的核心内容是正态分位数转换（Normal Quantile Transform，NQT）[83]。令Q表示标准正态分布，q表示相应的标准正态密度函数。则Hn与Sn转换后的正态分位数分别为

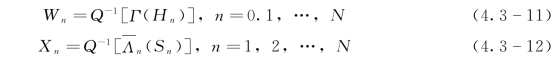
式中：Wn与Xn分别为Hn和Sn的正态分位数；Γ和Λn分别为Hn和Sn的边缘分布函数。

由式（4.3-11）、式（4.3-12）看出Γ（Hn）具有一致的分布，即Wn服从标准正态分布。

求得Hn和Sn的正态分位数Wn和Xn后，就可以在转化空间里对Wn和Xn进行分析，构造先验分布与似然函数，并求解出后验密度函数[84]。

1）先验分布。对Wn的估计方法有马尔可夫过程、最近邻抽样回归模型等。考虑到计算的简便性，假定转化空间中的实际流量过程服从一阶马尔可夫过程的正态-线性关系，具体为

式中：c为参数，Ξ为不依赖于Wn-1的残差系列，且服从N（0，1-c2）的正态分布。由此，可以求出Wn在Wn-1=wn-1的条件下的数学期望与方差：

同时，转化密度函数为

式中：q为标准正态密度函数；下标Q为该密度函数是在正态分位数转换空间里的密度分布。

对于任意时刻n，Wn的边缘密度函数为标准正态密度，即γQ=q。根据式（4.3-16）可以求得第n时刻的先验密度函数为

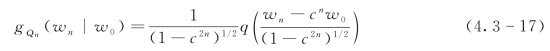
2）似然函数。假定转化空间中的各变量Xn、Wn、W0服从正态线性关系如下：

式中：an、bn和dn为参数；Θn为不依赖于（Wn，W0）的残差系列，并且服从N（0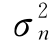，）的正态分布。

由此得到Xn以Wn=wn、W0=w0为条件的均值与方差：

即Xn在Wn=wn、W0=w0的条件下服从正态分布N（an wn+dn w0+bn，）。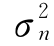

且有条件密度，即似然函数为

3）转化空间中的推导。综合先验密度和似然函数，得到转化后的Xn的期望密度函数为

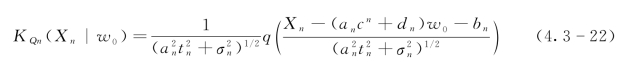
其中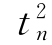，=1-c2n。可以得到Wn的后验密度函数：

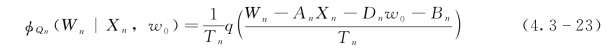
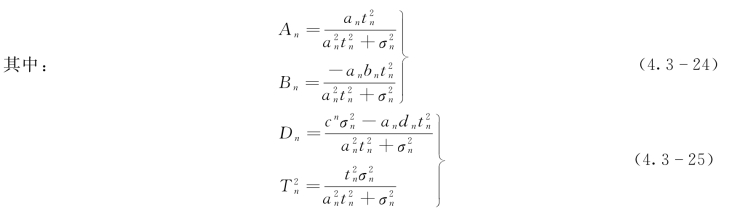
最后，采用全概率公式，由γQ=q和式（4.3-22），可得到Xn的边缘期望密度函数：

其中，。除非bn=0、τn=1，否则λQn（Xn）≠q。

（3）原始空间中的模型。由于转化空间中的所有密度函数rQ、gQn、fQn、κQn、φQn和λQn均属于高斯函数族，因此原始空间里的各密度函数r、gn、fn、κn、φn、λn就属于亚高斯函数族。对_于任意原始变量Y（Hn或Sn）、边缘分布函数M（Γ或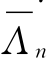）以及相应的密度函数m（γ或λn），原始空间和转化空间里的两个密度函数族是通过正态分位数转换NQT相互联系的，两者之间的Jacobian变换为

根据在预报时刻给出的条件H0=h0可得到Hn的亚高斯先验密度函数：

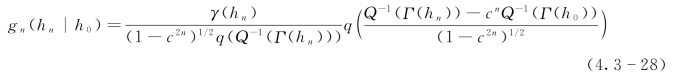
相应的亚高斯先验分布函数为

在构造先验密度族的过程中用到流量Hn的边缘分布函数Γ和相应的密度函数γ，以及（Wn，Wn-1）的一阶皮尔逊相关系数c，因为（Wn，Wn-1）的联合分布是正态的，所以参数c足以描述Wn和Wn-1之间的随机相互关系。同样，在亚高斯分布里，参数c也足以描述原始流量Hn和Hn-1之间的随机相互关系。

可以推广，cn是Wn和W0之间的k阶皮尔逊相关系数。因为|c|＜1，所以当式（4.3-29）中的时间n趋向于无穷大时，就会有Gn（·|h0）→Γ，这说明亚高斯模型是收敛的。

在预测流量Sn=sn和实测流量H0=h0的条件下，在原始空间里的实际流量Hn的亚高斯后验密度函数为

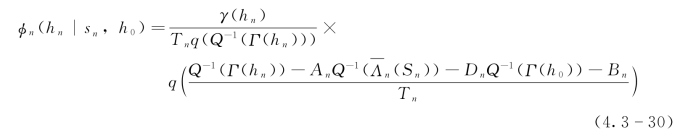
相应的亚高斯后验分布函数为

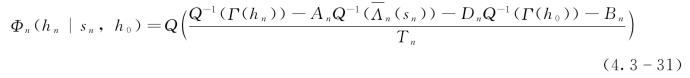
其中的相关参数已经在式（4.3-24）和式（4.3-25）中给出。

4.3.1.2　改进的概率洪水预报PCA-HUP模型

为推求预报量后验分布的解析解，传统HUP模型结合亚高斯模型，在正态空间中对先验分布式（4.3-13）和似然函数式（4.3-18）进行线性假设，并采用最小二乘法对相关参数进行估计。

然而，由于似然函数式（4.3-18）的自变量之间存在明确的线性关系，必然导致回归方程的多重共线性问题。若采用传统最小二乘法进行参数估计，会使得估计的回归系数不唯一，也使得回归方程不稳定（原始数据的极小变化可造成参数估计值和标准差的明显变化）。因此，本书结合主成分分析技术（Principal Components Analysis，PCA），对传统HUP模型进行改进，提出PCA-HUP模型。

主成分回归的基本思想：对原始回归变量进行主成分分析，将线性相关的自变量转化为线性无关的新的综合变量，采用新的综合变量建立模型回归方程。

（1）主成分分析。设X=（X1，…，Xp）T是p维随机向量，均值E（X）=μ，协方差阵D（X）=∑。

考虑它的线性变换：

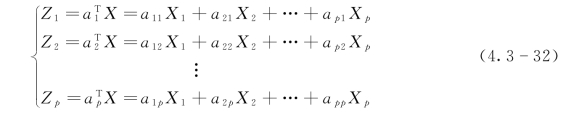
用矩阵表示为

由式（4.3-33）可以将p个X1，X2，…，Xp转化为p个新变量Z1，Z2，…，Zp，若新变量Z1，Z2，…，Zp满足下列条件：

1）Zi和Zj相互独立，i≠j，i，j=1，2，…，p。

2）Var（Z1）≥Var（Z2）≥…≥Var（Zp）。

3）=1，即+…+=1，i=1，2，…，p。

则新变量Z1，Z2，…，Zp为X1，X2，…，Xp的p个主成分，且与Z1，Z2，…，Zp线性无关。

（2）主成分回归。实际问题中不同的变量经常具有不同的量纲，变量的量纲不同会使分析结果不合理，将变量进行标准化处理可避免这种不合理的影响。

对数据进行标准化，首先要得出样本标准差和样本均值，记sj为xj样本标准差，即是xj的样本均值，即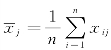，原始数据的标准化变换为

标准化后的数据矩阵为

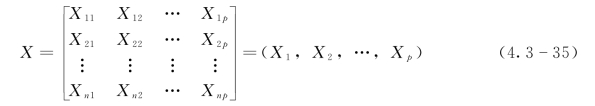
标准化后，X的相关系数阵也就是X的协方差阵（半正定矩阵）：

其中：λ1≥λ2≥…≥λp≥0为R的特征值，a1，a2，…，ap是相对应的单位正交特征向量，ap=（a1p，a2p，…，app）T。

主成分回归可以得到p个主成分，这p个主成分之间互相独立，且方差呈递减趋势，所包含的自变量的信息也是递减的。即主成分对因变量的贡献率是递减的，第i个主成分Zi的贡献率可以用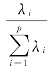来表示。

在实际问题的分析时，由于主成分的贡献率是递减的，后面的主成分贡献率有时会非常小，所以一般不选取p个主成分，而是根据累计贡献率来确定主成分个数，即前m个主成分的累计贡献率达到0.85时，选取前m个主成分进行回归。则原始回归问题转化为以下回归问题：

其中

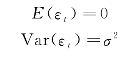
回归模型的矩阵形式为

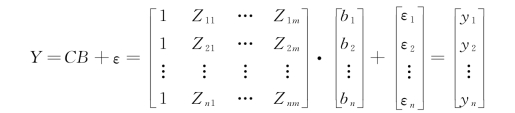
采用最小二乘法估计参数矩阵B，根据式（4.3-32）和式（4.3-34）可以估计因变量矩阵Y与自变量矩阵X之间的回归系数矩阵。

由此可见，主成分回归模型是对普通的最小二乘估计的改进，首先选取主成分，克服自变量间的多重共线性，然后对所选的主成分进行线性回归，进而得到主成分回归方程。

4.3.1.3　淮河干流PCA-HUP模型应用

本书分别以经验相关模型和新安江模型为确定性预报模型，在此基础上，采用PCAHUP模型分别对上述两个模型预报的可靠度进行定量，并在淮河干流主要控制断面王家坝、润河集和鲁台子进行了实际应用，以2002年和2005年洪水作为验证，采取滚动预报方式实现了洪水概率预报。

（1）王家坝。

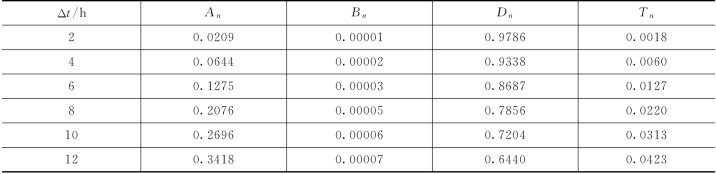
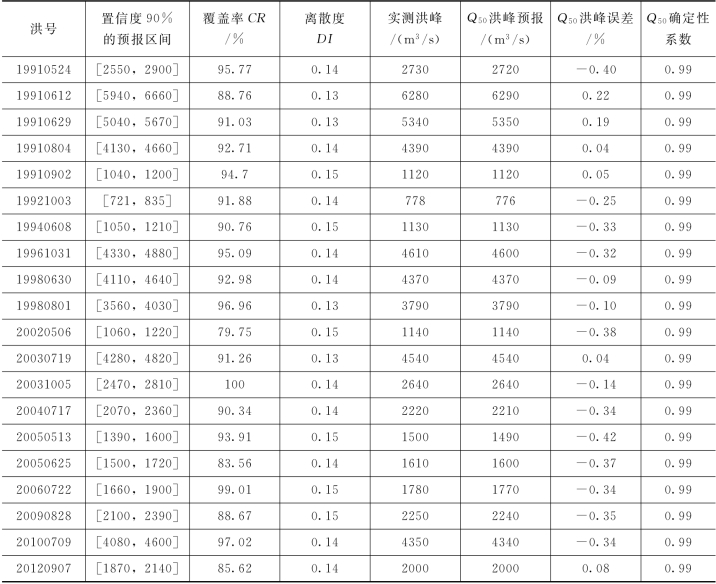
1）基于经验相关模型的概率预报结果。将前文所述经验相关模型的预报结果与实测资料输入PCA-HUP模型中，其中20场洪水用于相关参数的率定，8场洪水用于模型验证。模型相关参数见表4.3-1。以置信度为90%（亦可采用其他置信度值）的预报区间为例，对概率预报结果进行评估，同时，对流量分布函数的中位数Q50进行分位数评价，率定期PCA-HUP模型的模拟精度见表4.3-2。

表4.3-1　PCA-HUP模型参数（王家坝）

(www.daowen.com)

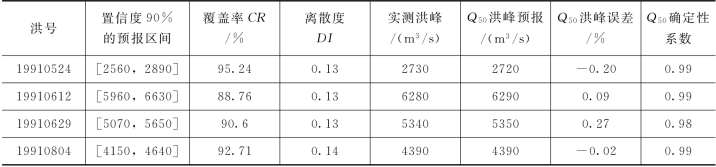
表4.3-2　PCA-HUP模型率定期模拟精度（王家坝，Δt=2h）

续表

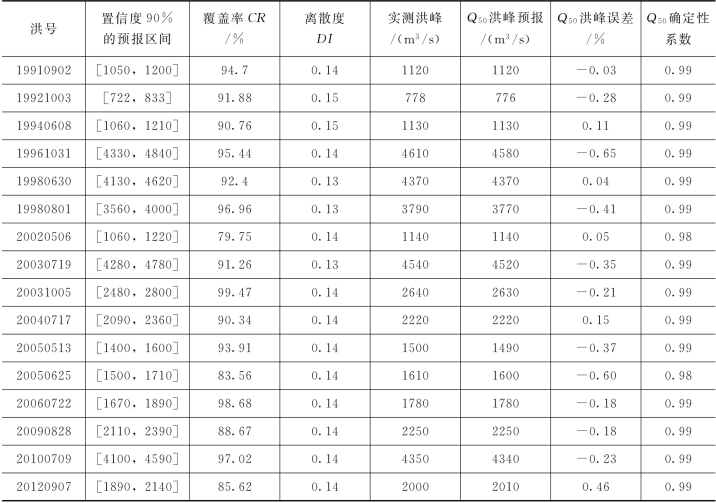
由表4.3-2可知，PCA-HUP模型率定期模拟结果：预报区间（置信度为90%）覆盖率基本在80%以上，且离散度在0.20以内。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高。

采用验证期8场洪水对概率预报模型进行检验，推求预报流量的概率分布，实现王家坝断面的洪水概率预报。预报精度统计见表4.3-3，预报流量过程线见图4.3-3和图4.3-4。由表4.3-3和两场洪水概率预报过程线可知，PCA-HUP模型（以经验相关模型为确定性预报模型）提供的概率预报结果：预报区间（置信度为90%）覆盖率较高，且离散度在0.2以内，说明在相对较小的区间宽度内，预报区间仍然能够覆盖绝大多数实测数据，概率预报精度较高。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，明显高于经验相关模型，充分体现了贝叶斯修正原理。且从不同预见期的预报过程线中可以看出，随着预见期的逐渐增大，区间宽度呈现出递增的趋势。

表4.3-3　PCA-HUP模型验证期概率预报精度（王家坝，Δt=2h）

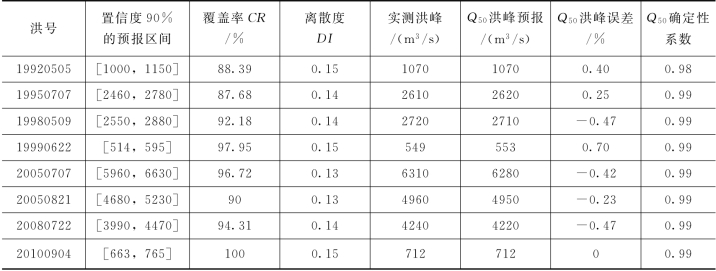
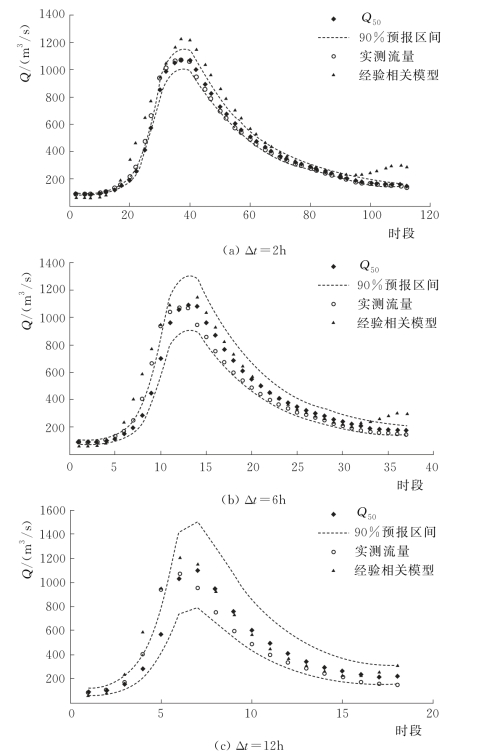
图4.3-3　19920505号洪水预报过程线（王家坝）

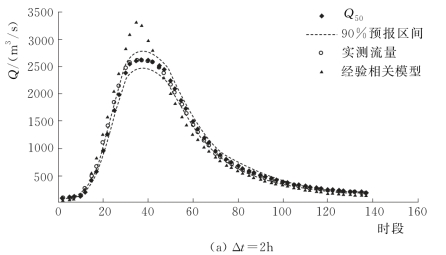
图4.3-4　（一） 19950707号洪水预报过程线（王家坝）

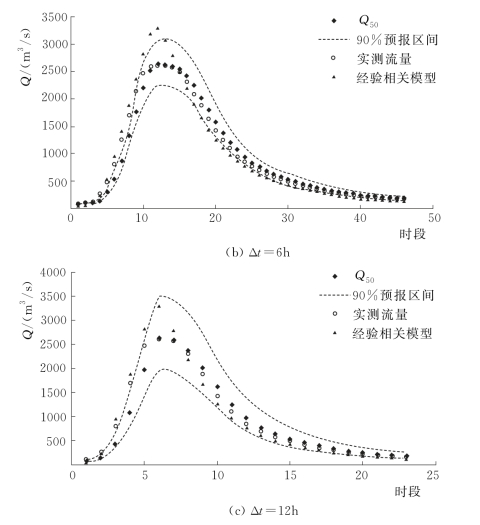
图4.3-4　（二） 19950707号洪水预报过程线（王家坝）

2）基于新安江模型的概率预报结果。将前文所述新安江模型的预报结果与实测资料输入PCA-HUP模型中，其中20场洪水用于相关参数的率定，8场洪水用于模型验证。模型相关参数见表4.3-4。以置信度为90%（亦可采用其他置信度值）的预报区间为例，对概率预报结果进行评估，同时，对流量分布函数的中位数Q50进行分位数评价，率定期模型的模拟精度见表4.3-5。

表4.3-4　PCA-HUP模型参数（王家坝）

续表

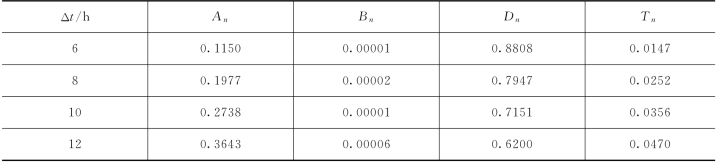
表4.3-5　PCA-HUP模型率定期模拟精度（王家坝）

由表4.3-5可知，PCA-HUP模型率定期模拟结果：预报区间（置信度为90%）覆盖率较高，且离散度在0.2以内。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，且从不同预见期的模拟过程线中可以看出，随着预见期的逐渐增大，区间离散度呈现出递增的趋势。

采用验证期8场洪水对概率预报模型进行检验，推求预报流量的概率分布，实现王家坝断面的洪水概率预报。预报精度统计见表4.3-6，限于篇幅，预报流量过程线以其中两场为例，见图4.3-5和图4.3-6。

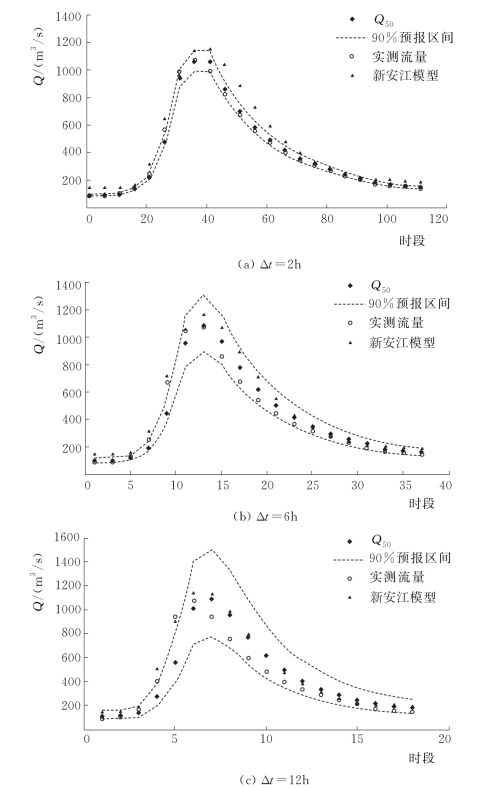
图4.3-5　19920505号洪水预报过程线（王家坝）

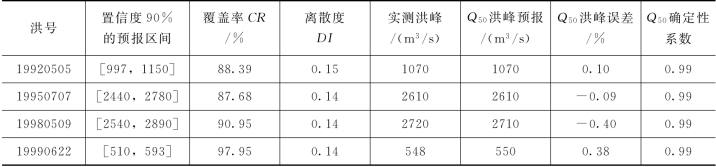
表4.3-6　PCA-HUP模型验证期概率预报精度（王家坝）

续表

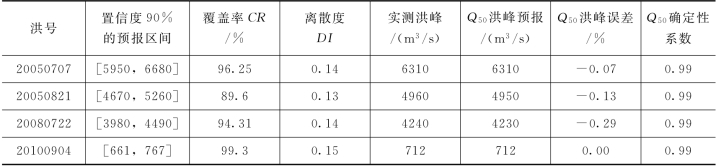
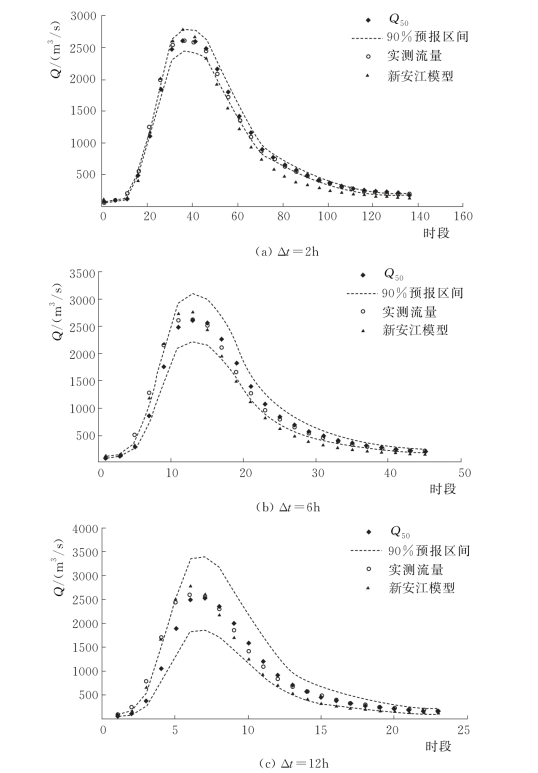
图4.3-6　19950707号洪水预报过程线（王家坝）

由表4.3-14和两场洪水概率预报过程线可知，PCA-HUP模型（以新安江模型为确定性预报模型）提供的概率预报结果：预报区间（置信度为90%）覆盖率在87%以上，且离散度在0.2以内，说明在相对较小的区间宽度内，预报区间仍然能够覆盖绝大多数实测数据，说明概率预报精度较高。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，明显高于新安江模型预报结果，充分体现了贝叶斯修正原理。且从不同预见期的预报过程线中可以看出，随着预见期的逐渐增大，区间宽度呈现出递增的趋势。

（2）润河集。

1）基于经验相关模型的概率预报结果。将前文所述经验相关模型的预报结果与实测资料输入PCA-HUP模型中，其中22场洪水用于相关参数的率定，8场洪水用于模型验证。模型相关参数见表4.3-7。以置信度为90%（亦可采用其他置信度值）的预报区间为例，对概率预报结果进行评估，同时，对流量分布函数的中位数Q50进行分位数评价，率定期PCA-HUP模型的模拟精度见表4.3-8。

表4.3-7　PCA-HUP模型参数（润河集）

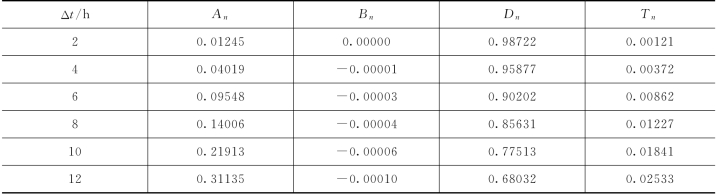
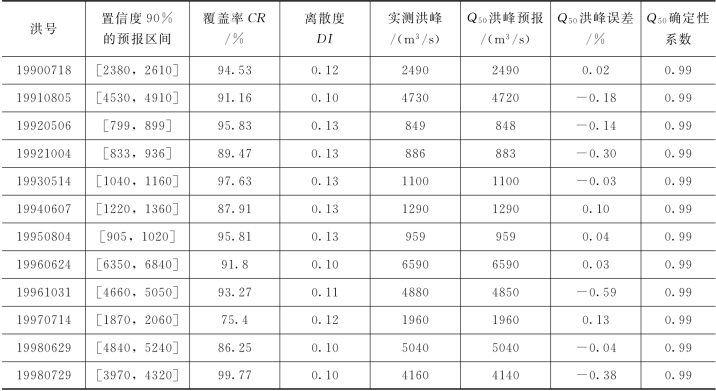
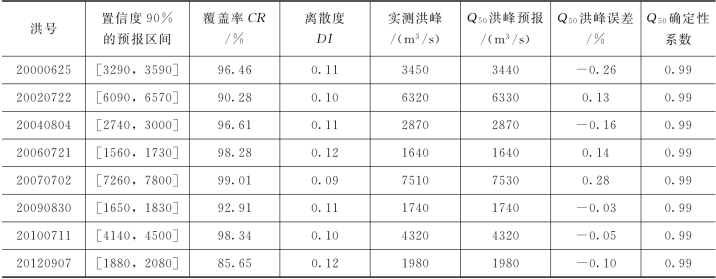
表4.3-8　PCA-HUP模型率定期模拟精度（润河集，Δt=2h）

续表

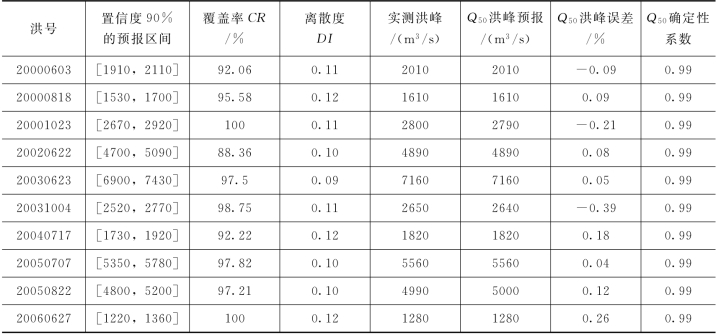
由表4.3-8可知，PCA-HUP模型率定期模拟结果：预报区间（置信度为90%）覆盖率较高，且离散度在0.2以内。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，且从不同预见期的模拟过程线中可以看出，随着预见期的逐渐增大，区间离散度呈现出递增的趋势。

采用验证期8场洪水对概率预报模型进行检验，推求预报流量的概率分布，实现润河集断面的洪水概率预报。预报精度统计见表4.3-9，限于篇幅，预报流量过程线以其中两场为例，见图4.3-7和图4.3-8。

表4.3-9　PCA-HUP模型验证期概率预报精度（润河集，Δt=2h）

由表4.3-19和两场洪水概率预报过程线可知，PCA-HUP模型（以经验相关模型为确定性预报模型）提供的概率预报结果：预报区间（置信度为90%）覆盖率较高，且离散度在0.2以内，说明在相对较小的区间宽度内，预报区间仍然能够覆盖绝大多数实测数据，概率预报精度较高。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，明显高于经验相关模型，充分体现了贝叶斯修正原理。且从不同预见期的预报过程线中可以看出，随着预见期的逐渐增大，区间宽度呈现出递增的趋势。

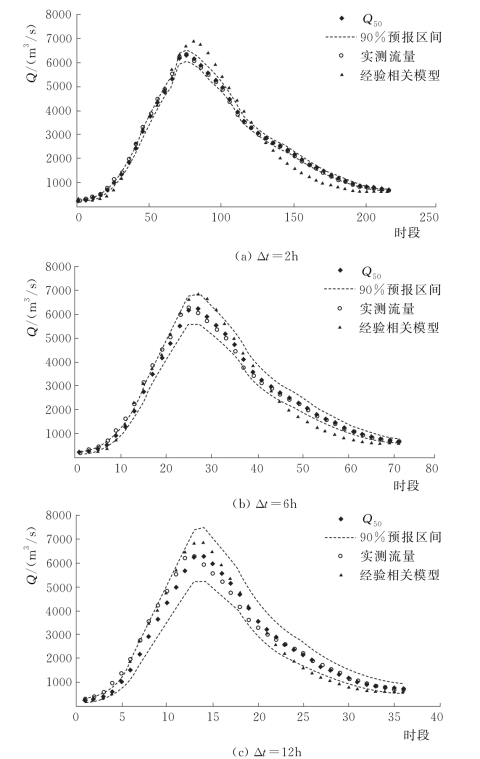
图4.3-7　20020722号洪水预报过程线（润河集）

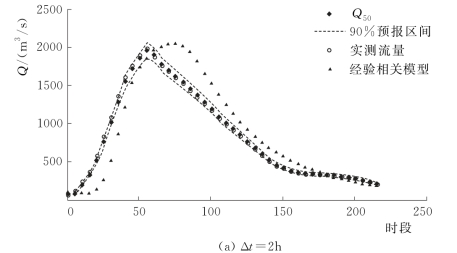
图4.3-8　（一） 20120907号洪水预报过程线（润河集）

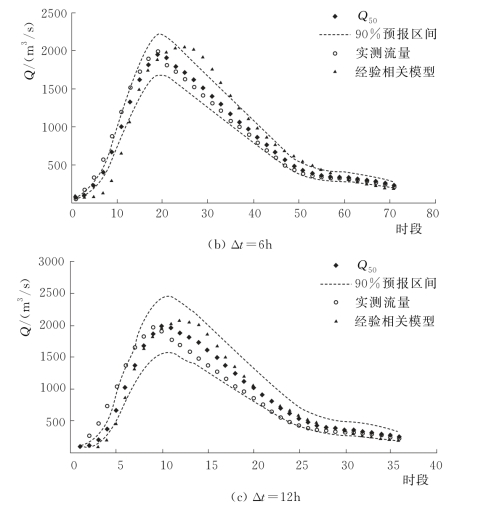
图4.3-8　（二） 20120907号洪水预报过程线（润河集）

2）基于新安江模型的概率预报结果。将新安江模型的预报结果与实测资料输入PCA-HUP模型中，其中22场洪水用于相关参数的率定，8场洪水用于模型验证。模型相关参数见表4.3-10。以置信度为90%（亦可采用其他置信度值）的预报区间为例，对概率预报结果进行评估，同时，对流量分布函数的中位数Q50进行分位数评价，率定期模型的模拟精度见表4.3-11。

表4.3-10　PCA-HUP模型参数（润河集）

表4.3-11　PCA-HUP模型率定期模拟精度（润河集，Δt=2h）

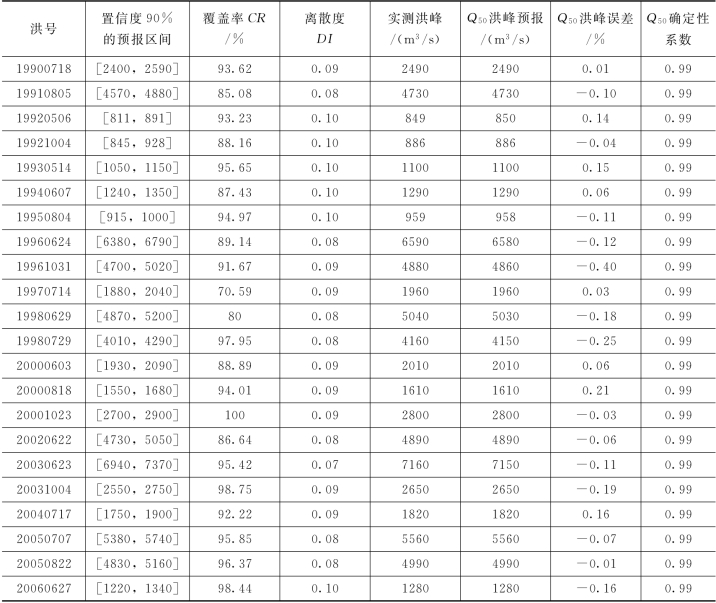
由表4.3-11可知，PCA-HUP模型率定期模拟结果：预报区间（置信度为90%）覆盖率在70%以上，且离散度在0.1以内。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，且从不同预见期的模拟过程线中可以看出，随着预见期的逐渐增大，区间离散度呈现出递增的趋势。

采用验证期8场洪水对概率预报模型进行检验，推求预报流量的概率分布，实现润河集断面的洪水概率预报。预报精度统计见表4.3-12，限于篇幅，预报流量过程线以其中两场为例，见图4.3-9和图4.3-10。

表4.3-12　PCA-HUP模型验证期概率预报精度（润河集，Δt=2h）

续表

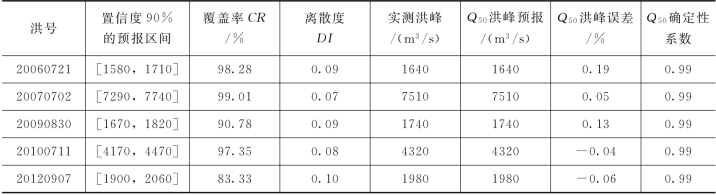
图4.3-9　20020722号洪水预报过程线（润河集）

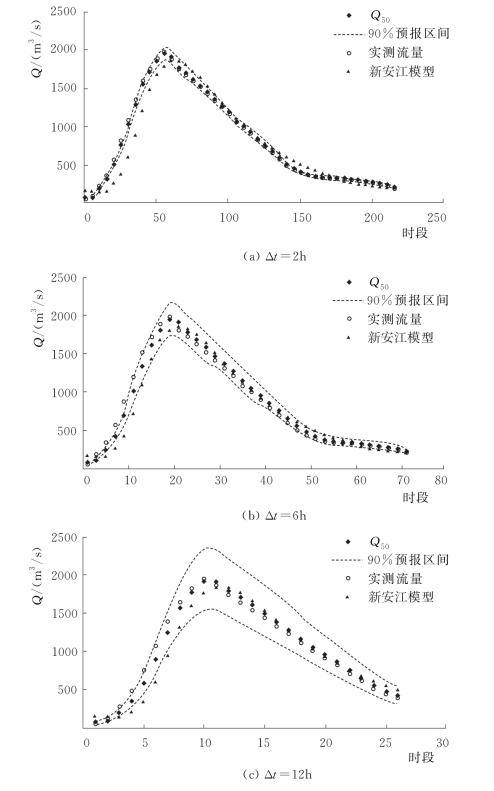
图4.3-10　20120907号洪水预报过程线（润河集）

由表4.3-12和两场洪水概率预报过程线可知，PCA-HUP模型（以新安江模型为确定性预报模型）提供的概率预报结果：预报区间（置信度为90%）覆盖率为83%以上，且离散度在0.1以内，说明在相对较小的区间宽度内，预报区间仍然能够覆盖绝大多数实测数据，概率预报精度较高。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，明显高于新安江模型，充分体现了贝叶斯修正原理，且从不同预见期的预报过程线中可以看出，随着预见期的逐渐增大，区间宽度呈现出递增的趋势。

（3）鲁台子。

1）基于经验相关模型的概率预报结果。将经验相关模型的预报结果与实测资料输入PCA-HUP模型中，其中12场洪水用于相关参数的率定，4场洪水用于模型验证。模型相关参数见表4.3-13。以置信度为90%（亦可采用其他置信度值）的预报区间为例，对概率预报结果进行评估，同时，对流量分布函数的中位数Q50进行分位数评价，率定期PCA-HUP模型的模拟精度见表4.3-14。

表4.3-13　PCA-HUP模型参数（鲁台子）

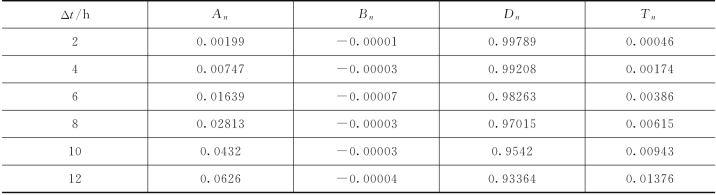
表4.3-14　PCA-HUP模型率定期模拟精度（鲁台子，Δt=2h）

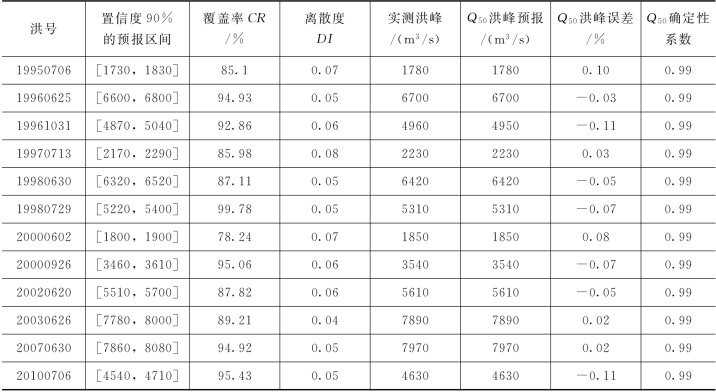
由表4.3-14可知，PCA-HUP模型率定期模拟结果：预报区间（置信度为90%）覆盖率较高，且离散度在0.1以内。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，且从不同预见期的模拟过程线中可以看出，随着预见期的逐渐增大，区间宽度呈现出递增的趋势。

采用验证期4场洪水对概率预报模型进行检验，推求预报流量的概率分布，实现鲁台子断面的洪水概率预报。预报精度统计见表4.3-15，限于篇幅，预预报流量过程线以其中两场为例，见图4.3-11和图4.3-12。

表4.3-15　PCA-HUP模型验证期概率预报精度（鲁台子，Δt=2h）

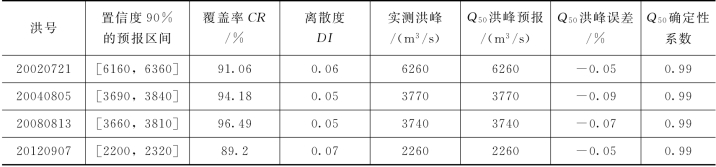
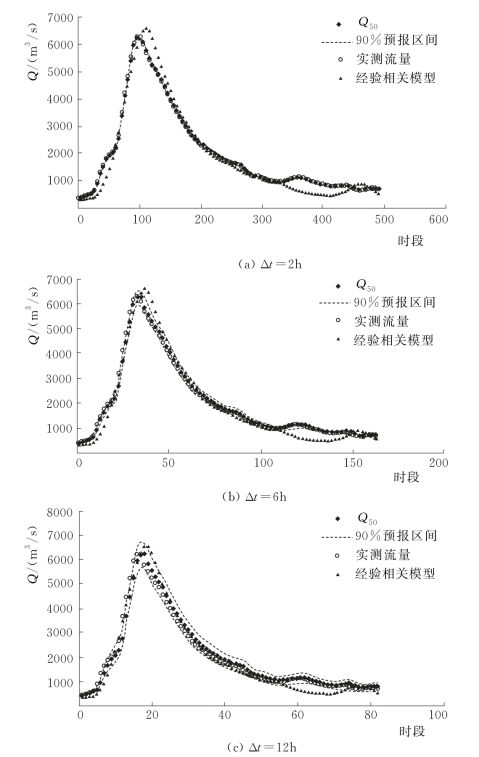
图4.3-11　20020721号洪水预报过程线（鲁台子）

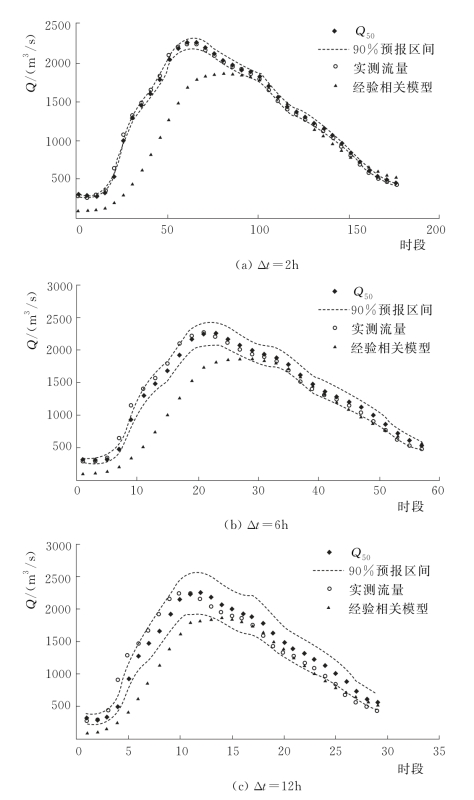
图4.3-12　20120907号洪水预报过程线（鲁台子）

由表4.3-15和两场洪水概率预报过程线可知，PCA-HUP模型（以经验相关模型为确定性预报模型）提供的概率预报结果：预报区间（置信度为90%）覆盖率较高，且离散度在0.1以内，说明在相对较小的区间宽度内，预报区间仍然能够覆盖绝大多数实测数据，概率预报精度较高。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，明显高于经验相关模型，充分体现了贝叶斯修正原理，且从不同预见期的预报过程线中可以看出，随着预见期的逐渐增大，区间离散度呈现出递增的趋势。

2）基于新安江模型的概率预报结果。将新安江模型的预报结果与实测资料输入PCA-HUP模型中，其中12场洪水用于相关参数的率定，4场洪水用于模型验证。模型相关参数见表4.3-16。以置信度为90%（亦可采用其他置信度值）的预报区间为例，对概率预报结果进行评估，同时，对流量分布函数的中位数Q50进行分位数评价，率定期模型的模拟精度见表4.3-17。

表4.3-16　PCA-HUP模型参数（鲁台子）

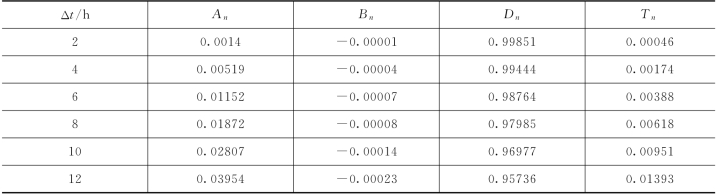
表4.3-17　PCA-HUP模型率定期模拟精度（鲁台子，Δt=2h）

由表4.3-17可知，PCA-HUP模型率定期模拟结果：预报区间（置信度为90%）覆盖率较高，且离散度在0.1以内。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，且从不同预见期的模拟过程线中可以看出，随着预见期的逐渐增大，区间宽度呈现出递增的趋势。

采用验证期4场洪水对概率预报模型进行检验，推求预报流量的概率分布，实现鲁台子断面的洪水概率预报。预报精度统计见表4.3-18，限于篇幅，预报流量过程线以其中两场为例，见图4.3-13和图4.3-14。

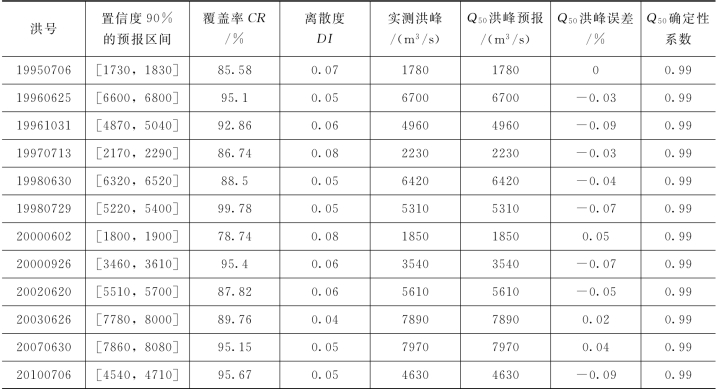
表4.3-18　PCA-HUP模型验证期概率预报精度（鲁台子，Δt=2h）

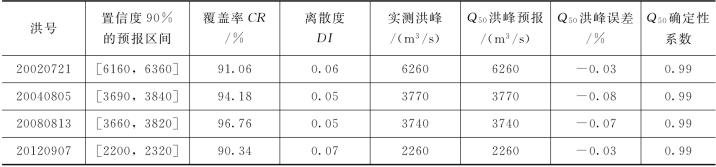
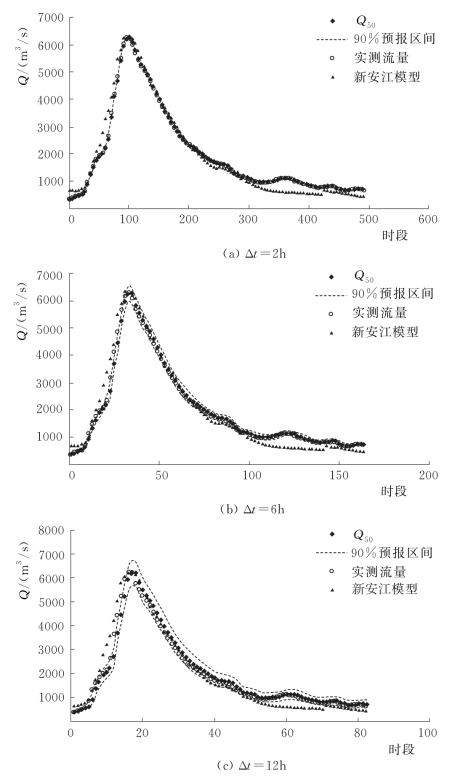
图4.3-13　20020721号洪水预报过程线（鲁台子）

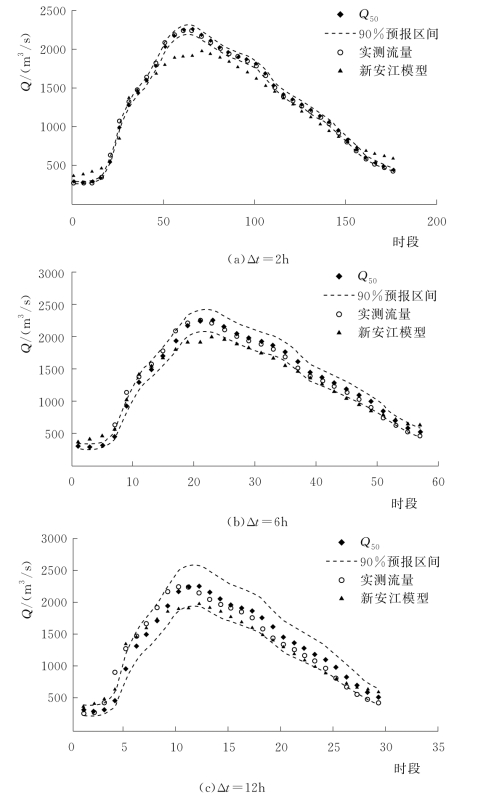
图4.3-14　20120907号洪水预报过程线（鲁台子）

由表4.3-18和两场洪水概率预报过程线可知，PCA-HUP模型（以新安江模型为确定性预报模型）提供的概率预报结果：预报区间（置信度为90%）覆盖率较高，且离散度在0.1以内，说明在相对较小的区间宽度内，预报区间仍然能够覆盖绝大多数实测数据，概率预报精度较高。此外，将每一时刻预报量概率分布的中位数预报与实测流量进行比较，确定性系数接近于1，洪峰误差在1%以内，说明中位数预报的精度非常高，明显高于新安江模型，充分体现了贝叶斯修正原理。且从不同预见期的预报过程线中可以看出，随着预见期的逐渐增大，区间宽度呈现出递增的趋势。