由于水文模型的参数率定中存在着历史水文资料误差、率定方法等影响因素，所以使得实际洪水预报中采用的一套“最优”模型参数未必总能提供准确的预报结果；同时由于水文模型存在的“异参同效性”，即两组不同的水文模型参数可以取得相同的预报效果。所以，水文模型参数的确定也存在着不确定性。这种不确定性的存在，必然导致预报结果也具有不确定性，因此需要对模型参数的不确定性进行概率描述，进而可以对相应的预报不确定性进行量化。

4.2.2.1　基于贝叶斯理论的水文模型参数后验分布估计

贝叶斯学派认为任何未知的参数θ都可以看作是一个随机变量，并可以用概率分布来描述任一变量的不确定性。贝叶斯推断的核心问题是先验分布的选择和后验分布的计算。先验分布，即总体分布参数θ的一个概率分布。贝叶斯学派从根本上来说，认为在关于任何总体分布参数θ的统计推断问题中，除了需要使用样本所提供的信息外，还必须指定一个先验分布，它是在进行参数统计推断时不可缺少的一个要素。后验分布则是在样本已知的条件下，根据样本的分布和所考虑参数的先验分布，用概率统计中求条件概率分布的方法，求出考虑参数的条件分布。由于这个分布是在采样以后才得到的，故称为后验分布。贝叶斯推断法的关键是任何推断都只需要相应的后验分布，而不再涉及样本分布。贝叶斯推理与经典估计方法相比，能更充分地利用样本信息和参数的先验信息，在进行参数估计时，由贝叶斯理论得到的估计量常常具有更小的平方误差或方差，能得到更精确的预测结果。

基于贝叶斯理论可获得模型参数的后验分布，从而可以对其不确定性进行定量分析。传统的贝叶斯公式为

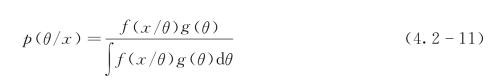
式中：θ和x分别为随机变量和与其相关的统计数据；p（θ/x）为后验概率密度函数；f（x/θ）为似然函数；g（θ）为后验分布。

对于水文模型来说，θ即为模型的敏感参数，x是模型的输出变量，即流量Q；并且将要进行水文模型预报所需要的其他要素，例如实测降雨、流量等资料记为w。则公式改写为

似然度函数f（Q/θ，w）的估计有多种方法，取如下形式：

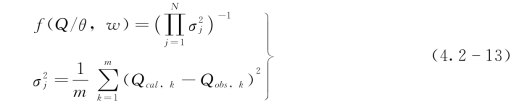
式中：Qcal，k、Qobs，k分别为计算和实测的流量值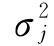；为第j场洪水误差的方差；m为第i场洪水的总时段数；N为次洪个数。

式（4.2-12）虽然形式简单，但是它的解不容易获得，而马尔可夫链蒙特卡罗方法（MCMC）即是为获得变量后验分布而发展起来的一种行之有效的计算方法，它的运用为推广贝叶斯推断理论方法的应用开辟了广阔的前景，使得传统的贝叶斯估计方法再度得到了复兴。流域水文模型的参数非线性和相关性特征导致了参数分布可能存在多个局部最优解和不连续可导点，采用传统的贝叶斯算法推求其显性联合概率分布十分困难，而MCMC法较传统的统计方法（如矩估计法，极大似然估计法等）就能更好地处理非线性复杂问题的求解。很显然，MCMC方法非常适用于对流域水文模型参数后验分布的推算[74，75]。

4.2.2.2　MCMC抽样

（1）马尔可夫链原理。马尔可夫链是指在数学中那些具有马尔可夫性质的关于离散时间的随机过程。令θt表示随机变量θ在t时刻、状态空间Θ上的取值，若θ在Θ内不同取值之间的转移概率（推荐分布）仅仅依赖于θ的当前状态，而与θ的过去状态无关，则称随机序列{θt，t≥0}为马尔可夫链。

令{θ（t）}t≥0是Θ上的齐次马尔可夫链，即P（·，·）与t无关，且转移概率函数为

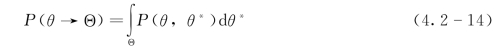
则称P（θ，θ*）是该马尔可夫链的转移核，即推荐分布。而对于某分布π（θ），满足：

其中∀θ*∈Θ，π（θ）是转移核P（θ，θ*）的平稳分布。当某个θj～π（θ），则θj～π（θ），j=t=1，…，从理论上讲，不管θ0选择何种分布，只要经过足够长的时间的搜索，θt的边缘分布就能达到平稳分布π（θ），也就是说，此时马尔可夫链收敛。而在马尔可夫链收敛之前的m次迭代中，各状态的边缘分布还不可认为就是平稳分布π（θ），因此在估计某个函数h（θ）时应该将前m个迭代值去除，即

式（4.2-16）也称为遍历平均。

（2）常用MCMC抽样方法简介。MCMC方法是基于贝叶斯理论的框架，通过建立平稳分布为π（θ）的马尔可夫链，并对其平稳分布进行采样，通过不断地更新样本信息从而使得马尔可夫链能够充分搜索整个模型参数空间，并最终收敛至高概率密度区，因而MCMC方法是一种近似的对理想的贝叶斯推断的过程。MCMC方法的关键是如何构造有效的推荐分布，以确保依据推荐分布抽取的样本收敛至高概率密度区。

所有蒙特卡罗方法其中一个基本步骤就是生成服从某个概率分布函数的伪随机样本。但是蒙特卡罗方法往往对于随机序列的模拟要求计算量很大，存在着计算复杂性的问题。人们对于感兴趣的变量x通常在Rk中取值，但有时也会在一个拓扑空间上取值。大多数应用中，在一个人们感兴趣的分布中生成独立样本是不可行的。在通常情况下，产生的样本要么是相关的，要么就是异于所要求的分布，或者两者同时发生。马尔可夫概念最初是由俄罗斯数学家Markov于1907年提出的，直至20世纪90年代，研究人员才将马尔可夫链蒙特卡罗方法（MCMC）引入到参数不确定性研究中，应用于待估参数后验分布的采样，使得收敛的速度明显提高。经过几代人的相继完善，已大大地减少了计算量，使得随机模拟在很多领域（物理、生物、气象、天文、计算机、化学、地理、通信等）的计算中显示出明显的优越性。马尔可夫链有其严格的数学定义，它的直观含义可理解为：在随机系统中下一个要达到的状态仅依赖于目前所处的状态，而与之前的状态无关。米特罗波利斯-哈斯汀算法（Metropolis-Hastings，M-H）是MCMC算法的基本框架，是一种从某一平稳分布的马尔可夫链中产生样本，然后使得所得的样本序列的概率分布收敛于目标后验分布函数的方法。因而，MCMC基本上是一种通过扩大马尔可夫链来获得相关样本的混合型蒙特卡罗方法。下面简单介绍常用的MCMC抽样方法。

1）Metropolis算法。米特罗波利斯算法（即Metropolis算法）是由Metropolis于1953年提出的一个算法[76]，其通过展开马尔可夫链来实现从分布π中采样。Metropolis算法是由以下两个步骤迭代形成的：令π（θ）=c exp{-h（θ）}是人们感兴趣的目标概率分布。

a.对当前的状态施加一个随机扰动，即θ（t）→θ′，这里的θ′可以看成是出自一个对称型概率转移函数T（θ（t），θ′），即T（θ（t），θ′）=T（θ′，θ（t））；计算改变量：

b.产生一个随机均匀分布数u～U[0，1]。若u≤exp（Δh），则令θ（t+1）=θ′；否则θ（t+1）=θ（t）。

Metropolis算法已在过去50年中被广泛应用于统计物理学中，它是被统计学术界采用和进一步发展的所有MCMC抽样方法的基石。

2）Gibbs抽样。Gibbs抽样方法是由German S和German D于1984年提出来的[77]，最初用于图像处理分析、神经网络和人工智能等大型且复杂数据的分析，后经Gelfand和Smith（1990）引入贝叶斯模型研究中，通过模拟进行积分运算，这对贝叶斯方法的实际应用产生了很深远的影响。Gibbs抽样的成功在于它能利用满条件分布（full conditional distribution）将关于多个相关参数的复杂问题降低成每次只需要处理一个参数的更为简单的问题。由于非常容易实现，在许多MCMC的统计应用中使用Gibbs抽样。Gelfand和Smith进行了总结并提供了一种贝叶斯计算方法，即将感兴趣的未知参数θ的概率密度表示为P（θ）=F（θ），其中F（θ）是θ的累积分布函数（CDF），联合密度、条件密度及边缘密度函数分别写作P（θ，η）、P（θ/η）和P（η）。

3）Metropolis-Hastings算法。上文已简单介绍了由Metropolis提出的一种转移核（transition kernel）的方法，随后Hastings对其加以推广，形成了Metropolis-Hastings方法[78]。一些文献研究了Gibbs与Metropolis采样方法相结合的问题，例如在Gibbs采样中利用Metropolis法抽取随机数，Best、Gilks和Tan（1995）提出了基于Gibbs采样的一种自适应舍选Metropolis采样方法（Adaptive Rejection Metropolis Sampling，ARMS）[79]，这种采样方法在贝叶斯分析中有很大的应用价值。

Metropolis-Hastings算法的关键是如何确定参数的推荐分布并进行参数相关性的处理。对于复杂的模型来说，参数只有较少的先验信息，且算法推荐分布的选择也存在较大的不确性，参数的最大后验概率密度函数的推求也就非常困难，造成算法收敛速度缓慢。下面简单介绍MetroPolis-Hastings算法的步骤。

a.任意给定初始点θ（t），且满足h（θ（t））＞0；

b.根据推荐分布Z（θ/θ（t））产生候选样本θ（t+1）；

c.计算接受率α，公式如下

d.Z是根据均匀分布u～U[0，1]产生的随机数；如果Z≤α，接受新样本θ（t+1）；反之，当Z＞α，令θ（t+1）=θ（t），并返回第二步。

上述步骤中，θ代表模型参数；t代表抽样次数；h（θt）代表目标函数，在本书中表示新安江水文模型的计算过程；Z（θ/θ（t））即代表模型参数的先验分布。

4）自适应Metropolis算法（AM算法）。为了解决Metropolis-Hastings算法存在的搜索速度慢的问题，Haario等（2001）提出了一种自适应的Metropolis算法[80]。相比传统的Metropolis-Hastings算法，自适应Metropolis算法不用事先确定参数的推荐分布，而是由后验参数的协方差矩阵来估算。后验参数的协方差矩阵能够自适应地调整于每一次迭代过程后。第i步参数的推荐分布假设定义为均值θi，协方差Ci的多元正态分布形式。协方差矩阵的计算公式见式（4.2-18）。

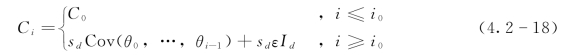
式中：C0为初始协方差，在初始采样次数i≤i0时，为了消除算法初始阶段的采样不稳定影响，协方差Ci取固定值C0；ε为一个较小的常数，以确保Ci不成为奇异矩阵；sd为比例因子，其依赖于参数的空间维度d，经常取sd=（2.4）2/d；Id为d维单位矩阵。

第i+1次迭代时，协方差计算公式可由式（4.2-19）推得

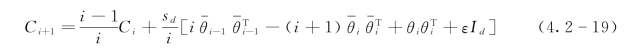(www.daowen.com)

其中，θi-1和θi分别为前i-1次和前i次迭代参数的均值。

AM算法的计算步骤如下：

a.设置初始化迭代次数i0；

b.利用式（4.2-19）计算Ci；

c.产生推荐参数值θ～N（θi，Ci）；

d.根据式（4.2-20）计算接受概率α；

e.产生随机数u～U[0，1]；

f.若u≤α则接受θi+1=θ*，否则θi+1=θi；

g.重复b～f步骤，直到产生足够的样本为止。

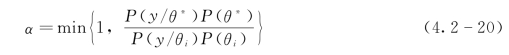
理论上来说，一个各向同性的采样器在t→∞时一定收敛，然而在实际应用中人们总是希望找到最小t值。为了实现此目标，本书现采用German S和German D于1992年提出来的收敛诊断指标（比例缩小得分），以解决多序列是否收敛，其计算公式如下

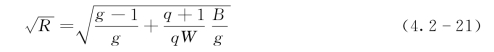
式中：g为每一个参数采样序列的迭代次数；q为用于评价的序列数；B/g为q个序列的平均值的方差；W为q个序列的方差的平均值。

根据式（4.2-21）计算每个参数的比例缩小得分，如果接近于1即表示参数收敛到了后验分布上。

4.2.2.3　模型参数不确定性定量分析

通过黄泥庄流域新安江模型的参数率定过程，发现河网消退系数（CS）较为敏感，因此本书针对参数CS进行参数不确定性分析。其中式（4.2-11）的先验分布均取三角分布。似然函数取如下计算式：

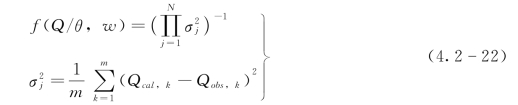
式中：N为洪水场次；m为流量过程的总时段数；Qcal，k为第k时刻的计算流量值；Qobs，k为第k时刻的实测流量值。

AM算法的配置为：参数CS的取值范围为[0.01，0.99]，初始取值设为0.45；参数初始协方差矩阵C0为对角矩阵，方差取参数取值范围的1/100。即CS的初始协方差矩阵是以0.098为协方差的对角矩阵；初始迭代次数i0=100次。算法平均运行5次，每次采样1000个样本。初始化阶段次数设为400次，以消除抽样初期的不稳定性。

图4.2-11和图4.2-12表示参数CS采样序列的平均值和方差的变化过程。

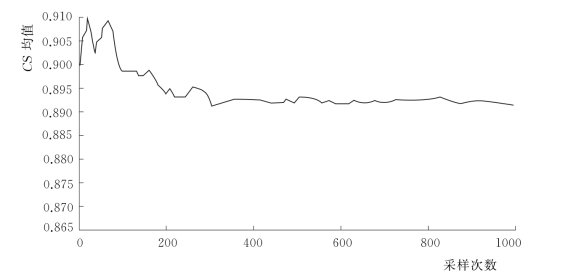
图4.2-11　参数CS的均值采样过程

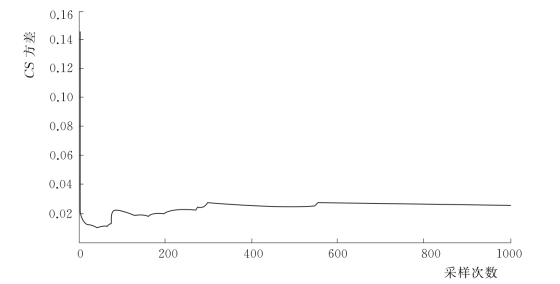
图4.2-12　参数CS的方差采样过程

由图4.2-12和图4.2-13可以看出，当抽样次数i＞400后，参数CS的平均值和方差基本达到稳定，因此可以判定采样过程是收敛的；且由此可以判断，将初始化阶段次数设为400次可以充分保证参数后验分布的稳定性。

利用式（4.2-21）计算的收敛指标判断演化过程见图4.2-13。

由图4.2-13可知，在迭代初期（i＜200），趋于稳定，并接近于1.0，说明参数CS的MCMC采样序列均能稳定收敛到其参数的后验分布，且算法全局收敛。将每一个序列的前400次舍去，这样5次平行试验共采集了3000个样本用于参数后验分布的统计分析。图4.2-14为参数CS的后验分布图。

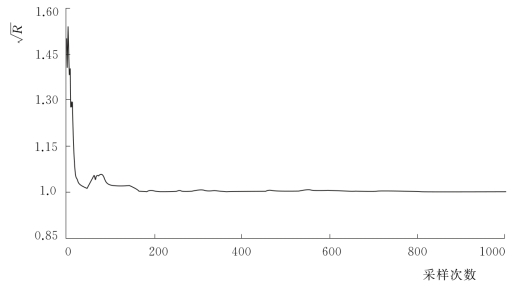
图4.2-13　参数CS的收敛指标演化趋势

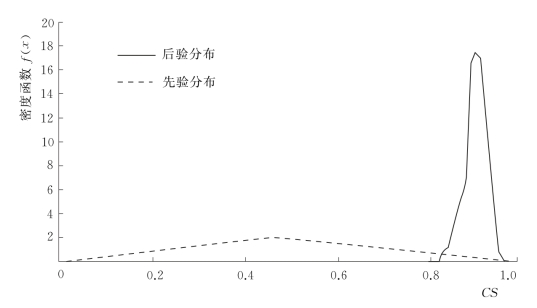
图4.2-14　参数CS的后验分布

经过MCMC抽样求得的参数CS的后验分布并未明显地说明参数服从哪一个分布，因此，本书根据后验分布的离散形式，统计其特征值，这里仅以均值的最大似然估计和众数为例。表4.2-2即为参数CS经过MCMC抽样最终确定的后验分布的特征值。

表4.2-2　河网蓄水消退系数（CS）后验分布特征值

将经过MCMC抽样的CS的每一组取值分别代入新安江模型计算，从而得到每个时刻的3000个流量计算结果，由此可以估计预报流量的概率分布，实现概率预报。不仅可得到一定置信度的区间预报结果（以置信度为90%为例，其他置信度亦可得到），同时，将参数概率分布的特征值带入新安江模型，还可以得到特征值预报（如中位数、众数等，仅以均值的最大似然值为例）。考虑模型参数不确定性的洪水概率预报结果见表4.2-3和图4.2-15～图4.2-20。

表4.2-3　考虑模型参数不确定性的洪水概率预报

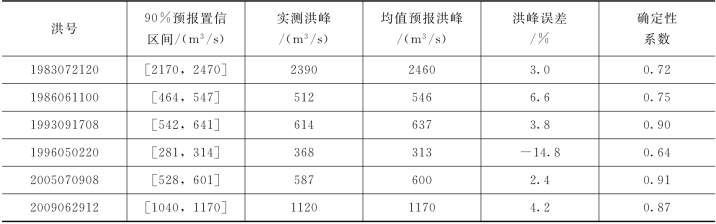
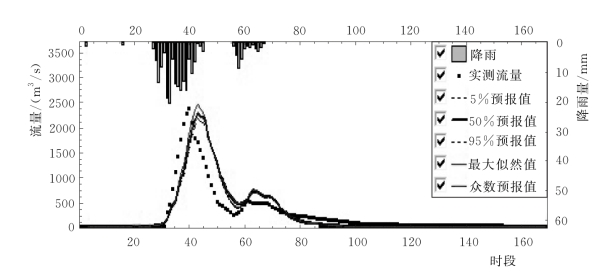
图4.2-15　1983072120号洪水考虑模型参数不确定性的概率预报过程线

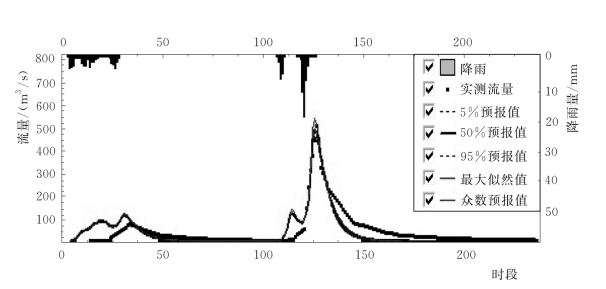
图4.2-16　1986061100号洪水考虑模型参数不确定性的概率预报过程线