4.2.1.1　面雨量计算不确定性

目前，水文预报中作为模型输入的面雨量由流域内雨量站点的点雨量计算而来，虽然计算方法在不断改进，但由于雨量站点布设数目有限，由点雨量推求面雨量必然存在因雨量站数目不足或代表性不高而导致的面雨量计算误差[70]。

一般可以假设面雨量的计算值P （t）与实际未知“真值”之间的误差ε（t）服从均值为0、方差为σ2的正态分布：

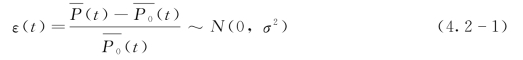
由式（4.2-1）可知，当面雨量的计算值已知时，误差ε（t）与面雨量“真值”是一一对应的函数关系（t代表面雨量过程的任一时段）。进一步可以推得

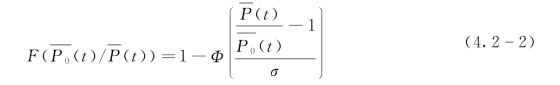
为了估计标准差σ，对随机变量ε（t）进行标准化处理：令u（t）=，即u（t）为面雨量计算误差的标准化变量，且u（t）～N（0，1）。

当误差标准化变量的保证率为η[即分布u（t）中置信度取η]时，可知（图4.2-1）：

图4.2-1　标准正态分布概率密度函数示意图

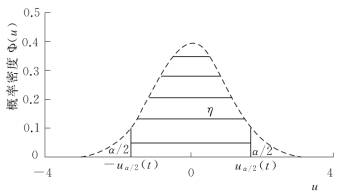
式中：α为u（t）中对应于置信度η的显著性水平，即α=1-η；uα/2（t）为标准正态分布的双侧α的分位点。

可以推得

式中：Eη为保证率取η的允许误差。

以误差保证率η=90%为例[即分布u（t）中置信度取90%]，α/2=0.05，Φ（u（t））=0.95，查标准正态分布函数表可知，uα/2（t）=1.64，根据式（4.2-4）可得

式中：E90%为保证率取90%的允许误差。

综合式（4.2-2）和式（4.2-4）可知，以面雨量计算值P（t）为条件的面雨量“真值”的概率分布为

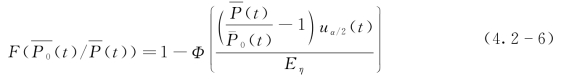
由式（4.2-6）可知，若得到允许误差Eη的估计值，即可获得面雨量“真值”P0（t）的条件概率分布的估计，进而实现面雨量计算不确定性的概率描述。

4.2.1.2　抽站法基本原理

（1）抽站法简介。抽站法是我国雨量站规划采用的主要方法，即利用雨量站网稠密地区的全部雨量资料计算面平均雨量的近似真值，然后按分布均匀的抽站原则抽去一部分雨量站，再计算面平均雨量及其误差，寻求误差与布站密度、统计时段和地形因素的关系，探讨满足精度要求的布站数量。1981—1994年，原水电部水文司等单位开展了梅雨区雨量站网密度实验研究，确认抽站法是一种稳定、合理的分析方法，简明直观，理论依据较强。此方法已列入了《水文站网规划技术导则》[71]。

假设研究流域内有N1处具有同步观测资料的雨量站，首先根据逐时段雨量资料，计算N1个站的1h、3h、6h、12h、24h共5个时段的面平均雨量，将其作为该计算单元响应时段面平均雨量的“真值”。然后按照下列步骤进行：

1）确定一个降雨时段，如取Δt=24h，根据同步观测资料有m1个样本数；确定一个抽站数目N2，从N1个站中抽取分布均匀的N2个站，求出Δt时段的面平均降雨量，再基于由N1个站计算出来的“真值”求误差εN2，i。注意，此时的εN2，i是由m1个数组成的样本数组。

2）选定不同误差标准，例如分别选取5%、10%和15%，计算出在不同误差标准下的面平均降雨量误差的合格保证率。

3）再次从N1个站中抽取第i（i=1，2，…，n）组N2个站，按照步骤1）和步骤2）计算各第i组的基于不同面平均降雨量误差标准的合格保证率。

4）针对不同误差标准（5%、10%和15%），分别算出n组抽站对应的平均合格保证率。

5）按照步骤1）～步骤4）分别求出不同时段、不同抽站数目在不同误差标准下的面平均降雨量的平均合格保证率。

根据以上抽站法的主要步骤，可作出研究区域在1h、3h、6h、12h、24h共5个时段不同误差标准（5%、10%、15%）下得到的平均保证率结果图（图4.2-2为Δt=24h不同允许误差下的保证率图）。平均保证率为90%对应的站数N，即为研究流域的合理布站数。可利用插值法得到对应于平均保证率为90%的站数N。

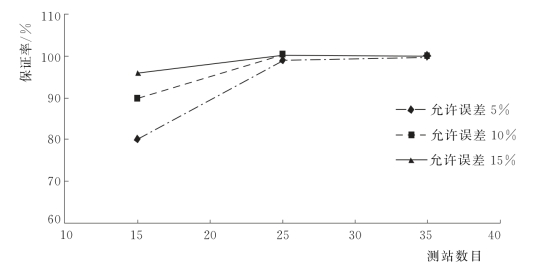
图4.2-2　24h降雨不同允许误差下的保证率

（2）抽站法经验公式。在同一地区、同一雨型及同一气象条件下，各块面积所需要站数目还与下垫面的条件有关。1981年，建立了中国梅雨雨量站网密度实验区，实验区选在江西省境内最大暴雨区之一的怀玉山南侧，暴雨量及暴雨频次都较多。实验区范围是以乐安河支流洎水流域为主体，向南向北扩展面积为1280km2。实验区建成209个雨量站。雨量站间距离不超过4km，1983—1988年收集了大量的野外试验数据，得出雨量站网密度公式计算所需配套雨量站数公式为[72，73]

式中：N为所需站数，站；A为流域面积，km2；H为流域平均高程，m；T为降雨时段长，h；E为保证率90%的面平均雨量允许误差，取10%～15%。

式（4.2-7）经江西省其他流域和浙江、湖南、福建、湖北等流域的雨量资料和流量资料进行验证，都得到了满意的结果。因此，该公式作为对中小河流水文站（A≤2000km2）分析计算雨量站网密度的经验公式被写入了《水文站网规划技术导则》。

4.2.1.3　流域面雨量概率分布估计(www.daowen.com)

利用抽站法经验公式，即式（4.2-7），在已知雨量站布站数目、降雨计算时长、流域地形因素等情况下，可以反推保证率为90%的允许误差E90%：

结合式（4.2-6）和式（4.2-8），可以推得以面雨量计算值为条件的面雨量“真值”的概率分布：

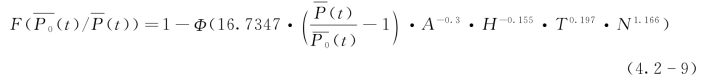
式中变量符号意义同前。

本书选取黄泥庄流域作为研究区域，流域面积为805km2；流域平均高程H=479m；流域内雨量站个数N=12个；该研究计算步长T=1h。由此可得到黄泥庄流域在现有站网规划条件下面平均雨量真值与面平均雨量计算值的相对误差在保证率为90%下的取值为

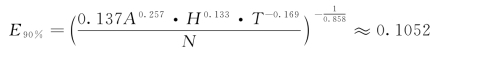
根据式（4.2-5）可得到相对误差概率分布的方差为

由式（4.2-9）可得到黄泥庄流域在现有站网条件下面雨量“真值”的条件分布函数为

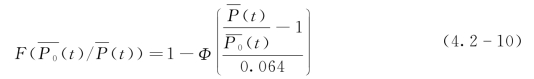
对于任意一场降雨过程，当任一时段的面雨量计算值P （t）已知时，由式（4.2-10）可以推求该时段面雨量“真值”的概率分布函数。图4.2-3为19830723号洪水降雨过程及各时段面雨量“真值”的分布函数示意图。以其中第6时段的降雨为例，该时段面雨量计算值P （t）=20.9mm，根据式（4.2-10）可以推得该时段面雨量“真值”的概率密度函数，见图4.2-4，图中f（x）表示概率密度。

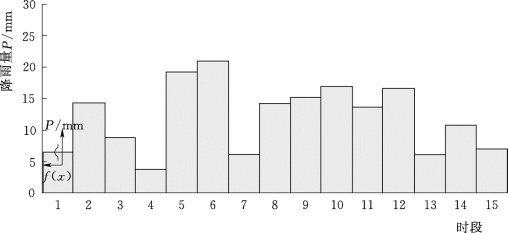
图4.2-3　19830723号洪水降雨过程示意图

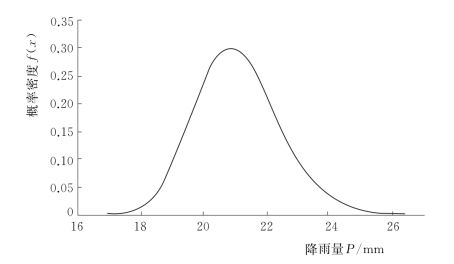
图4.2-4　19830723号洪水第6时段面雨量“真值”的概率密度函数

4.2.1.4　考虑面雨量计算不确定性的洪水概率预报

对于每一个降雨时段，都可以估计出其面雨量真值的概率分布，下面简述如何根据该降雨量概率分布作出洪水概率预报。

（1）从各时段面雨量的概率分布中随机抽取一个值，组成一组面雨量数值，将其作为一场降雨过程的估值。

（2）将估计的这场降雨过程代入确定性水文模型（本书选取三水源新安江模型作为确定性水文模型），计算得到对应的流量过程。按照上述随机抽样方法，抽若干次，例如10000次，便可得到10000场流量过程数据。

（3）将每一时刻10000个流量值进行排序，即可得到均值预报及不同置信区间下的概率预报。

本次选取黄泥庄流域1980—2010年间六场洪水为例，采用式（4.2-10）描述面平均雨量“真值”的概率分布，并结合新安江模型，可以获得预报流量的分布函数，实现黄泥庄流域考虑降雨不确定性的概率预报。采用以上方法不仅可以得到具有一定置信度的区间预报结果（以90%置信度为例，亦可得到其他置信度），同时也可得到诸如期望值、中位数等的预报结果（仅以中位数Q50为例），概率预报精度统计见表4.2-1，预报过程线见图4.2-5～图4.2-10。

表4.2-1　考虑降雨不确定性的洪水概率预报结果

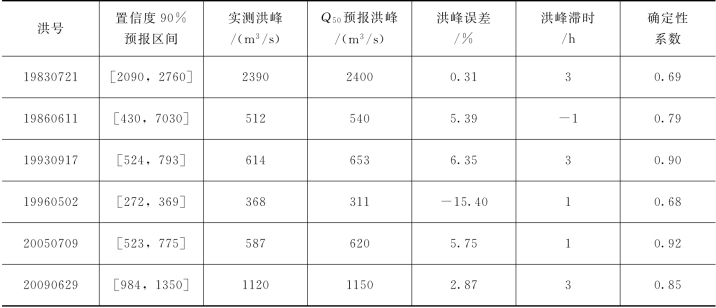
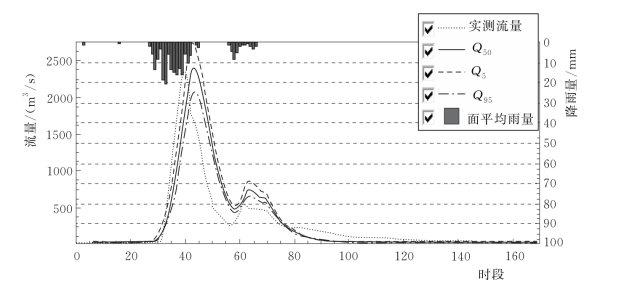
图4.2-5　1983072120号洪水考虑面雨量计算不确定性的概率预报过程线

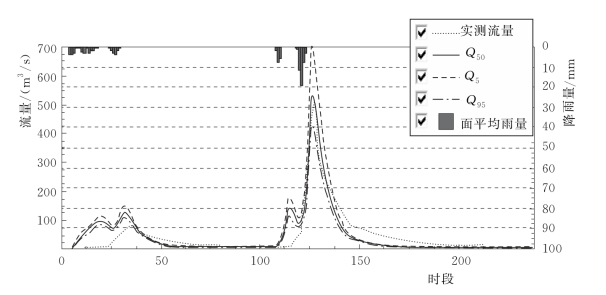
图4.2-6　1986061100号洪水考虑面雨量计算不确定性的概率预报过程线

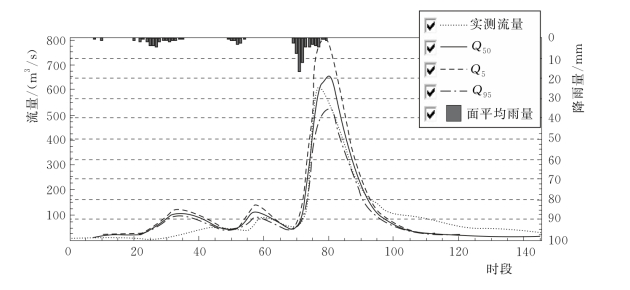
图4.2-7　1993091708号洪水考虑面雨量计算不确定性的概率预报过程线

图4.2-8　1996050220号洪水考虑面雨量计算不确定性的概率预报过程线

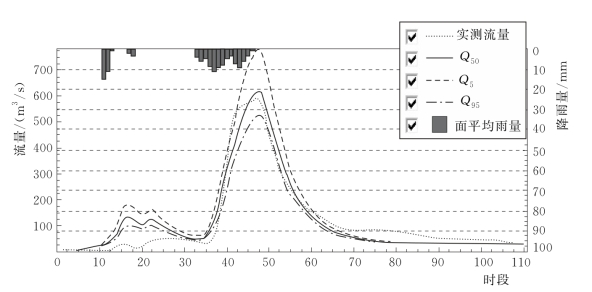
图4.2-9　2005070908号洪水考虑面雨量计算不确定性的概率预报过程线

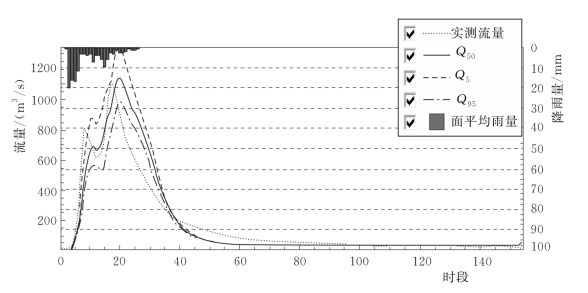
图4.2-10　2009062912号洪水考虑面雨量计算不确定性的概率预报过程线