3.4.5.1　模型的资料要求

（1）地理信息及河道大断面资料。

1）流域详细的河流水系、站网、水工建筑物、防洪控制工程等分布图。

2）需要充足且较新的断面资料，能够反映河道沿河床变化的真实情况。

王家坝到鲁台子距离140km，共403个断面，代表性断面见图3.4-5～图3.4-11。

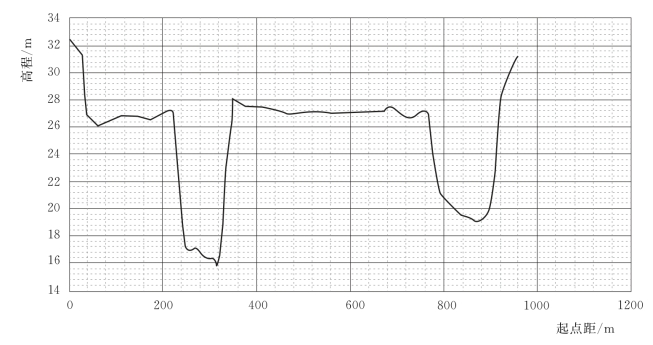
图3.4-5　王家坝河道断面图

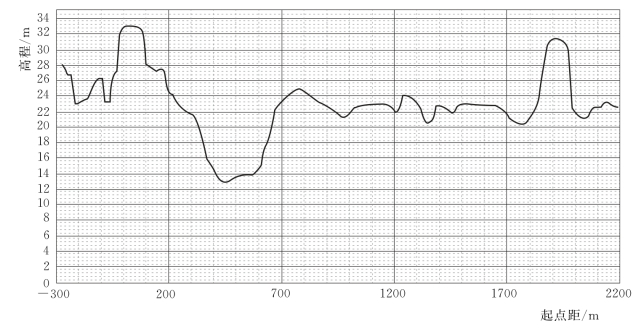
图3.4-6　南照集河道断面图

（2）水文资料。

1）流域内水文（水位）站的多年水位流量资料，包括洪水要素摘录、日资料等。

2）行蓄洪区的库容曲线和调度规则，分蓄洪区的水位面积、有效容积曲线等。

3）流域内雨量站的多年降雨资料，包括降雨要素摘录、日降雨资料。

4）流域内蒸发站的实测蒸发资料。

5）流域内的控制工程的历史实际运行资料，多年实际流量过程资料。

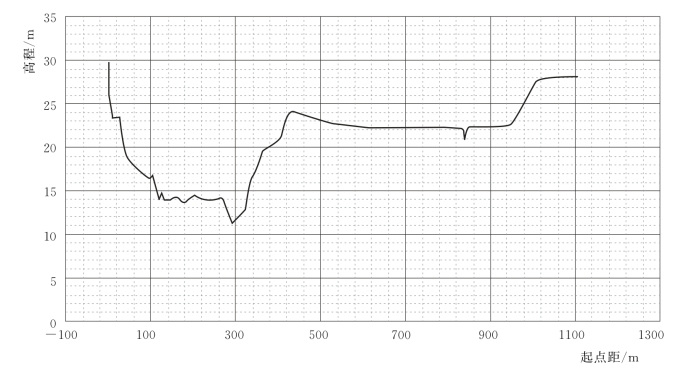
图3.4-7　润河集河道断面图

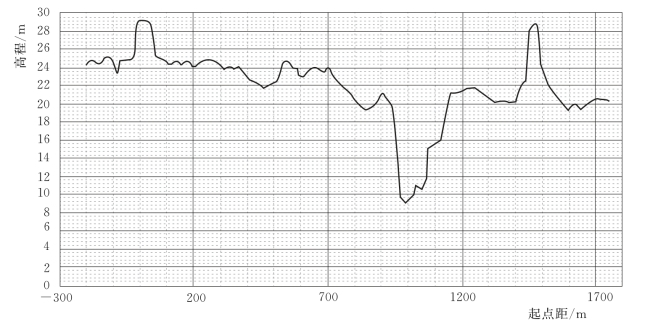
图3.4-8　汪集河道断面图

（3）实时资料。

1）流域内各雨量站的实时雨量资料，如果有条件能提供预见期预报雨量更好。

2）水文（水位）站的实时水位流量资料。

3）预报初始条件和边界条件下的水位或流量或水位流量关系数据。

4）控制工程运行情况。

3.4.5.2　主要问题的处理

图3.4-9　临淮岗上引河口断面图

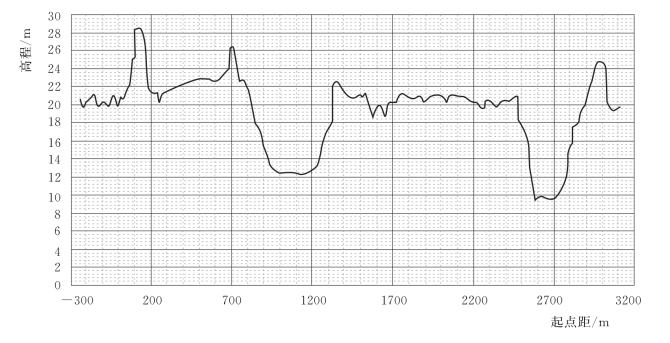
图3.4-10　正阳关断面图

（1）边界条件。水力学计算中，上边界一般采用流量过程，下边界一般采用水位过程或者水位流量关系作为定解条件。本书以鲁台子断面作为下边界断面，以该断面汛期的12场洪水（即鲁台子断面新安江模型率定期洪水）资料确定水位-流量关系，作为MIKE模型下边界，进行计算分析。图3.4-12为淮河干流鲁台子水位-流量关系曲线。

从图3.4-12可见，水位-流量关系曲线近似于线性的，取其近似的线性水位-流量关系作为下边界条件。(www.daowen.com)

（2）行蓄洪区和分洪道的处理。行蓄洪区、分洪道是重要的防洪设施，洪水预报调度模型需要对这些设施实际或者预计使用的效果进行计算模拟。建立符合行蓄洪区和分洪道特点的概化处理方法，对入流流量、出流时间和出流流量三个要素进行模拟计算，对河道的洪水预报精度有着较大的影响。

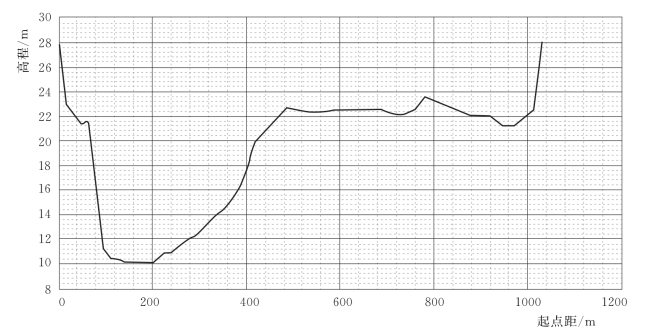
图3.4-11　鲁台子河道断面图

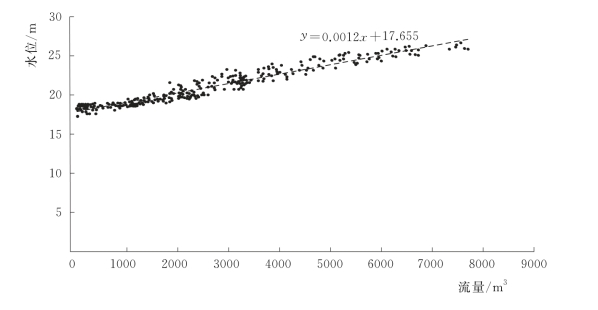
图3.4-12　淮河干流鲁台子的水位流量关系

在水力学模型中，行蓄洪区和分洪道的处理都是概化为源（汇）项，其区别在于概化的方法不同，本书根据行蓄洪区、分洪道运用方式的不同，采用了不同的处理方式，对于同种设施还提供了多种方式，在符合实际情况的同时，提高了系统的灵活性。

对于蓄洪区和有闸门控制的行洪区，可以将其视为一个零维的调蓄体，在洪水预报计算中，进出调蓄体的流量过程由实测和洪水调度设计方案得到。在计算中同时兼顾“蓄满出流”的原则，由有效蓄水容积和蓄洪流量过程确定蓄水开始排入干流的时间，出流流量过程采用设计的方案。

对于没有闸门控制的行洪区，模型中需要确定行洪区入口行洪流量、出口汇流时间和流量。入口流量过程一般采用分流比或者堰流公式确定。由于堰流公式需要实测资料率定系数，并且分洪属于侧向入流，堰流公式不完全适用，因此本书采用分流比的处理方法。洪水在行洪区内的演进比较复杂，出口汇流时间和流量与行洪区地形、下垫面条件和出口位置都有关系，本书采用简化的处理方法，以水量平衡为基础，由行洪区有效容积和行洪流量确定蓄满出流时间，出流流量即采用同时刻的入流流量，相比较而言，这种方法既具有一定的物理基础，实际处理也比较简单，在精度上也是可以接受的。表3.4-1为部分行洪区的蓄水量。

表3.4-1　部分行洪区蓄水量

3.4.5.3　流域分区

根据淮河流域地形、水系和水流的特点，可将淮河中游水系概化成如图3.4-13所示。将王家坝至鲁台子作为该水系的干流，河段中有5个行洪区，3个蓄洪区。王家坝流量过程为干流的上边界条件，鲁台子的水位-流量关系为干流的下边界条件，对润河集的流量进行预报。干流上的史灌河（蒋家集）、沙颍河（阜阳）和淠河（横排头）三条支流以及干流两侧无资料流域视为干流的集中入流。在干流上建有临淮岗闸，用以控制灌溉、排洪，可视为模型的内边界条件[6668]。

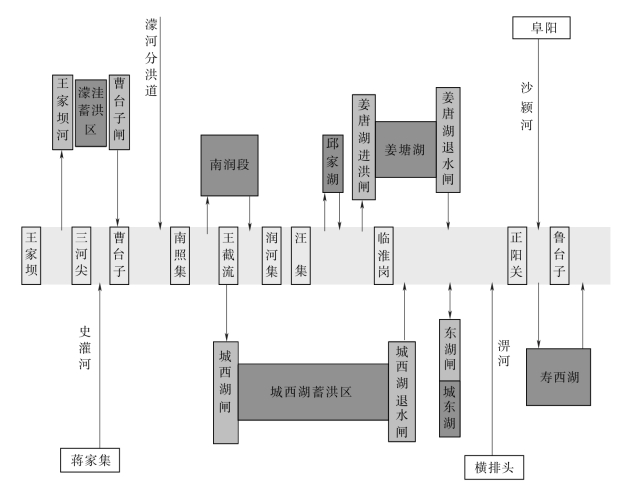
图3.4-13　王家坝至鲁台子河段概化图

3.4.5.4　模型预报精度

采用1990—2013年间24年的洪水资料对模型进行率定，以王家坝—鲁台子区间洪水为研究对象，选用1990—2013年共24年的资料进行计算，采用24场洪水资料进行次洪模型计算（其中18场用于率定，6场用于验证），Δt=2h，主河道糙率为0.033，率定期模拟精度见表3.4-2，限于篇幅，率定期洪水模拟过程线以其中两场为例，见图3.4-14和图3.4-15。

表3.4-2　润河集水力学率定精度

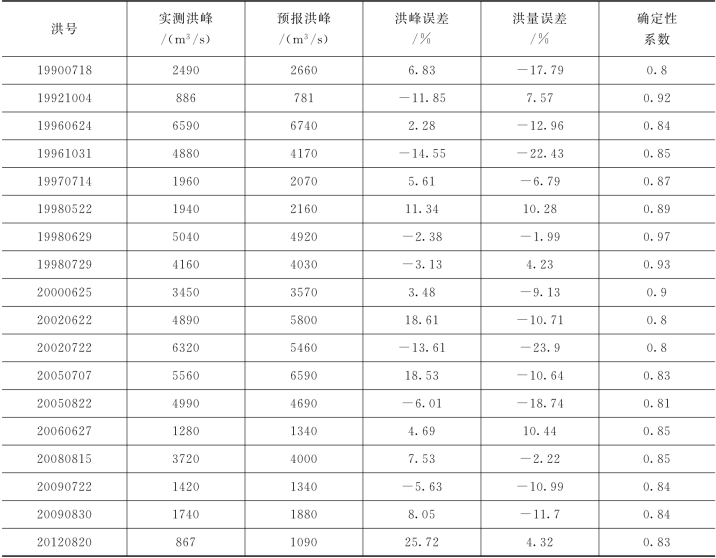
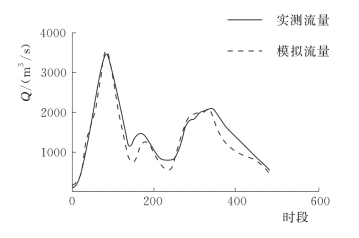
图3.4-15　20000625号洪水模拟过程线（润河集）

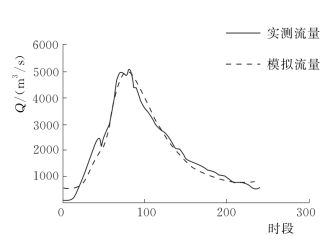
图3.4-14　19980629号洪水模拟过程线（润河集）

由表3.4-2可知，水力学模型率定期的洪峰误差除一场外均在20%以内，洪量误差除两场外均在20%以内，确定性系数均在0.8以上，说明率定期场次洪水的模拟精度较高，率定的参数可信度较高。模型验证期场次洪水预报精度见表3.4-3，限于篇幅，预报过程线以其中两场为例，见图3.4-16和图3.4-17。

表3.4-3　润河集水力学验证期预报精度统计表

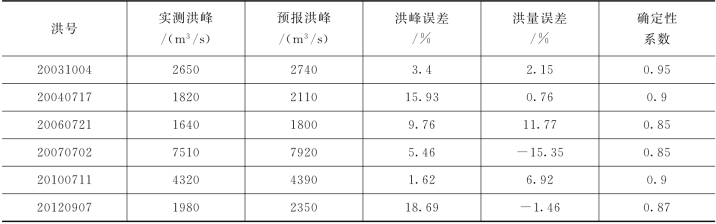
图3.4-16　20031004号洪水模拟过程线（润河集）

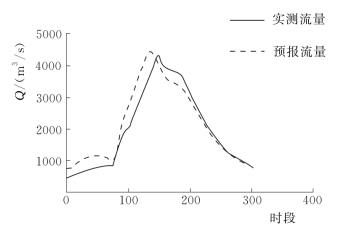
图3.4-17　20100711号洪水模拟过程线（润河集）

由表3.4-3和两场洪水预报过程线可知，验证期场次洪水的洪峰误差均在20%以内，洪量误差均在20%以内，确定性系数均在0.85以上，水力学模型的预报精度较高。