（1）河道方程。根据前述离散方程，河道内任意点的水力参数λ（水位Z或流量Q）与相邻网格的水力参数的关系可以表示为一线性方程：

式（3.4-17）中的系数可以分别由式（3.4-15）、式（3.4-16）计算。

假设一河道有n个网格点，因为河道的首末网格点总是水位点，所以n是奇数。对于河道的所有网格点写出式（3.4-17），可以得到n个线性方程：

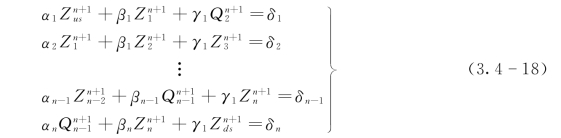
式中，第一个方程组中的Zus和最后一个方程中的Zds分别是上、下游汊点的水位。某一河道第一网格点的水位等于与之相连河段上游端汊点水位：Z1=Zus，即α1=-1，β1=1，γ1=0，δ1=0。同样，Zn=Zds，即αn=0，βn=1，γn=-1，δn=0。

对于单一河道，只要给出上下游水位边界，即Zus和Zds为已知，就可用消元法求解方程组（3.4-18）。

对于河网问题，由方程组（3.4-18），通过消元法可以将河道内任意点的水力参数λ（水位Z或流量Q）表示为上下游汊点水位的函数：

只要先求出河道各汊点的水位，就可以用式（3.4-19）求解任意河段、任一网格点的水力参数。

（2）汊点方程组。如图3.4-3所示，对于围绕汊点的控制体应用连续性方程得

将式（3.4-20）中右边第二个括号里的三项分别以式（3.4-19）代替，可得(www.daowen.com)

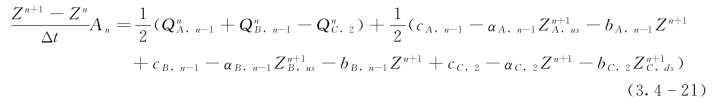
式中：Z为汊点的水位；ZA，us、ZB，us分别为支流A、B上游端汊点水位，ZC，ds为支流C下游端汊点水位。

在式（3.4-21）中，将某个汊点的水位表示为与之相连接的河道的汊点水位的线性函数。同样，对于河网所有汊点（假设为N个），就可以得到N个类似的方程（汊点方程组）。在边界水位或流量为已知的情况下，可以利用高斯消元直接求解汊点方程组，得到各个汊点的水位，进而代回式（3.4-19）求解任意河道、任意网格点的水位或流量。

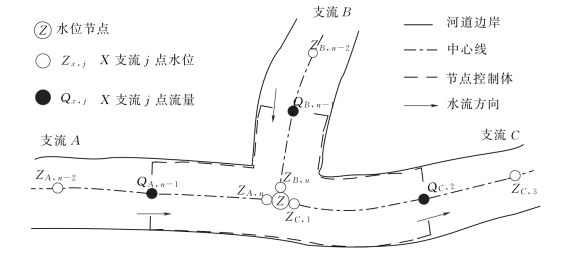
图3.4-3　河网汊点（以三汊点为例）

（3）外边界条件。若在河道边界点上给出水位的时间变化过程：Z=Z（t），此时，假设边界所在河道编号为j，边界上的汊点方程为

若在河道边界点上给出流量的时间变化过程：Q=Q（t），如图3.4-4所示的控制体，应用连续方程可得

图3.4-4　流量边界

若在河道节点上给出的是流量、水位关系Q=Q（Z），其处理方法同流量边界条件，得到与式（3.4-22）类似的方程，只是方程中由流量水位关系计算得到。