路径分析是一种统计程序，通过分析变量之间假设的因果效应，来测试研究人员提出的关于一套观察或者呈现变量之间因果关系的理论。该理论由美国遗传学家S.赖特于1921年首创，后被引入社会学的研究中，并发展成为社会学的主要分析方法之一。

路径分析的主要目的是检验一个假想的因果模型的准确和可靠程度，测量变量间因果关系的强弱，回答下述问题：(1)模型中两变量xj与xi间是否存在相关关系；(2)若存在相关关系，则进一步研究两者间是否有因果关系；(3)若xj影响xi，那么xj是直接影响xi，还是通过中介变量间接影响或两种情况都有；(4)直接影响与间接影响两者大小如何。

路径分析的主要步骤是：

第一，选择变量和建立因果关系模型，这是路径分析的前提。研究人员多用路径图形象地将变量的层次，变量间因果关系的路径、类型、结构等，表述为所建立的因果模型，如图1-4所示。

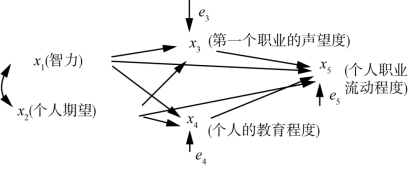
图1-4　路径分析图

图1-4中所示是五个变量因果关系的路径，图中带箭头的直线“→”连接的是具有因果关系的两个变量，箭头的方向与因果的方向相同。当两变量只有相关关系而无因果关系时，用弧线双向箭头表示。图中变量分为：(1)外生变量，因果模型中只扮演因，从不扮演果的变量，是不受模型中其他变量影响的独立变量，如x1与x2。(2)内生变量，模型中既可为因又可为果的变量，其变化受模型中其他变量的影响，如x3、x4与x5。(3)残差变量，来自因果模型之外的影响因变量的所有变量的总称，如e3、e4、e5。

若变量间的关系是线性可加的，则图中的因果模型可用三个标准化多元线性回归方程表示。

我们将pij称为由xj到xi的路径系数，它表示xj与xi之间因果关系的强弱，即当其他变量均保持不变时，变量xj对变量xi的直接作用力的大小。将pie称为残差路径系数，它表示所有自变量所不能解释的因变量的变异部分，其大小对于因果模型的确定有重要作用。

第二，检验假设。路径分析要以下列假定为前提：(1)变量间的因果关系是单向的，不具有反馈性，又称递归模型；(2)变量间具有线性可加关系；(3)变量具有等距以上测量尺度；(4)所有误差均为随机，外生变量无测量误差；(5)所有内生变量的误差变量间及与内生变量有因果关系的所有自变量间无相关。当某些假定，如递归性或变量的测量尺度不满足时，要做适当的处理才能应用路径分析。(www.daowen.com)

第三，估计参数。首先计算路径系数与残差路径系数，然后计算两变量之间相关系数rji。此外，要计算两变量之间总因果作用力，包括变量xj对xi的直接作用力、xj经中间变量而对xi的间接作用力两个部分。例如，图1-4的因果模型中，x1对x5的总作用力由直接作用力p51和间接作用力构成。这两部分作用力的大小可由两变量之间的相关系数rij的分解得到。最后还要计算决定系数嵀，它表示所有作用于xi的自变量所能解释xi变异量的比例，计算公式是：

第四，评估因果模型。评估的主要指标是：

(1)嵀，若嵀太小，则要考虑是否需要增加新的自变量，以保证模型精度。

(2)一个理想的因果模应当很小，当它很大时，则有必要重新估计此因果路径，也可由下式计算：

(3)进行F检验：

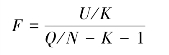
式中，Q为残差平方和，U为回归平方和，N为样本数，K为变量数，检验不显著时要修改模型。

路径分析是多元回归分析的延伸，与后者不同的是：第一，路径分析间的因果关系是多层次的，因果变量之间加入中介变量，使路径分析模型较一般的回归模型对于现实因果关系的描述更丰富有力；第二，路径分析不是运用一个而是一组回归方程，在分析时更应注意保证各方程式所含意义的一致性。