1.clump 生成理论

沥青混合料中粗集料颗粒形状是不规则的，为了使数值模拟更加真实，需要利用PFC 软件提供的clump 理论将小的圆形颗粒单元随机组合成大的不规则的“组合颗粒”单元，clump 理论为 PFC 模拟不规则颗粒提供了理论方法。由于 clump 是由多个球组成，则clump 的质量、形心位置、惯性矩分别为

式中　[ p]

m ——颗粒质量；

R [ p]——颗粒半径；

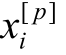——clump 的形心位置；

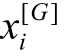——clump 的质心位置。

clump 的运动由作用于 clump 颗粒上的合力和矩向量决定。由于clump 被看作是一个刚体，因此clump 的运动可以用clump 颗粒上一点的平动和clump 的转动来描述。其平移方程为

式中　Fi 、 g i、 m ——作用于 clump 颗粒上的合力、由重力引起的体力加速度向量和clump 的总质量；

xi ——clump 的位置。

式中　——作用于p 颗粒上的外力和接触点c 上的力。

clump 的转动方程为

式中　Mi ——clump 质量中心的合力矩；

H i——clump 角动量的时间变化率。

合力矩Mi 可以由下式计算：

式中　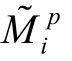——作用于颗粒p 上的外力矩；

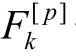——作用于颗粒上的合力；

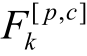——作用于颗粒p 接触点c 处的力。

角动量的时间变化率表达式为

此时 α i= 。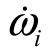

平动和转动加速度有限差分表达式为

将式（5-50）带入式（5-53），求得时间为(t+Δt/2)的速度表达式为

得到

写成矩阵形式为

其中：

式（5-57）提供了三个方程，其中有6 个未知量，这6 个未知量可以通过下边的迭代过程实现：

（1）令n=0 。

（2）令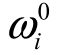等于最初的角速度。

（3）解（5-57）方程得到。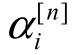

（4）在假定没有阻尼的情况下确定新的角速度

（5）将 iω 的估计值修改为

（6）令n = n+1 循环进行第（3）步。

数值试验表明经过四次迭代后就会收敛。

Clump 理论允许组合成颗粒的内部圆形颗粒间可以重叠，而且重叠量的多少没有限制，通过此理论可以根据需要组合成任意形状和尺寸的“组合颗粒”。在整个计算过程中，不考虑“组合颗粒”内部颗粒间的接触，“组合颗粒”形成后其颗粒性状及颗粒大小不会随外力的变化而变化，而且也不会在外力作用下而破裂。但是组合而成的颗粒之间及组合而成的颗粒与其他的颗粒单元间的接触、接触力不会受到影响，仍然满足力-位移定律及牛顿第二定律，也就是说每一个“组合颗粒”仍然是具有柔性边界的刚性多边形，并且在颗粒流模型“组合颗粒”中仍然被看作一个独立的颗粒单元。

2.多边形颗粒随机生成

本节依据蒙特卡洛方法，采用 PFC 软件内置的 FISH 语言开发并构建随机多边形颗粒模型。

（1）蒙特卡洛法理论简介。

蒙特卡洛方法（Monte Carlo Method），又称为随机抽样法、概率模拟法及统计试验法，是第二次世界大战中由美国参与研制原子弹的“曼哈顿计划”成员S. M. 乌拉姆和 J. 冯. 诺伊曼提出，并以赌城“摩纳哥

Monte Carlo”来命名，它是在以概率统计理论为指导的基础上发展起来的一种数值模拟计算方法。

根据大数定律，假设 x1 ，x2…xn 是n 个彼此之间相互独立的随机变量而且来自同一总体，其中均值及方差分别为μ 和σ ，那么对于任意的ε ＞ 0有(www.daowen.com)

另外，如果随机事件A 发生的概率为 P(A)，则在n 次独立的重复试验中，事件A 发生的频数为k，频率为W(A)=k/ n，则对于任意的ε ＞0 有

蒙特卡洛方法为从总体中随机抽取简单的样本进行抽样试验，如果抽取样本数量n 足够大，并且 根据概率收敛于μ ，则频率 k /n 根据概率收敛于 P(A)，这就是蒙特卡洛方法的理论基础[106]。

依据蒙特卡洛方法建立随机多边形集料模型的基本思路为：① 依据颗粒形态，计算颗粒的边界、颗粒的位置、颗粒的方位角等有关颗粒形态特征参数，然后构建统计模型；② 依据统计模型，采用随机抽样方法，给颗粒形态特征的每个参数赋一个值；③ 依据颗粒形态特征的每个参数，利用 PFC 自带的FISH 语言进行颗粒开发，构建随机多边形颗粒单元模型。

采用蒙特卡罗法产生满足一定分布要求的离散颗粒单元，首先要采用某种特定的算法产生该种分布的随机数，在数理统计上称为随机抽样。随机变量的不同分布对应的随机数序列也有所不同。但是就随机数产生过程而言，最基本的随机变量为在区间[0，1]上服从均匀分布。如果在区间[0，l]产生均匀的随机变量x，然后经过变换x ′= a + (b -a )x，可求得均匀分布在[a，b]的随机变量x′，那么由在区间[0，1]上均匀分布的随机变量的随机数就可以变换得到服从其他分布的随机变量的随机数。因此，在研究随机数产生方法时，只需要研究[0，1]上均匀分布随机变量的随机数产生方法即可。

（2）多边形颗粒随机生成。

由于多边形更能够反映沥青混合料中集料的不规则特性对沥青混合料性能的影响，因此借鉴文献[107,108]提供的不规则颗粒的生成方法生成不规则多边形。多边形由多边形边数、极半径以及极角等参数确定，如图5-21 所示。

图5-21　圆内接多边形颗粒

生成不规则颗粒之前先要按照级配生成圆盘颗粒，圆盘颗粒的半径为

式中　1r ——某一粒径组粒径的下限；

r2 ——某一粒径组粒径的上限；

α ——区间[0，1]上的随机数。

利用极坐标确定多边形的顶点

式中　kθ ——第k 边的对角；

bk ——区间[0，1]上的随机数；

δ ——小于1 的常数；

n——多边形的边数。

因为n 个 kθ 之和往往不等于2π，因此为了确保多边形是闭合的，需要对 kθ 进行修正：

生成的多边形的顶点坐标为

式中　α ——颗粒方位的相角，它是0 ～ π/2 均匀分布的随机数；

x 0——多边形外接圆圆心的横坐标；

y 0——多边形外接圆圆心的纵坐标。

（3）不规则多边形侵入关系的判别标准。

在模型投放随机多边形颗粒时，为避免随机多边形颗粒间出现重叠，需对其相互侵入关系进行判别，如图5-22。对于随机多边形P 和Q，当其满足以下条件时，二者必定相离：① P 的任意顶点均不在Q 中；② Q的任意顶点均不在P 中；③ P、Q 的任意两条边（线段）均不相交。具体的生成过程如图5-23 所示。

图5-22　多边形分离判别

图5-23　判断颗粒边界是否相交流程图

（4）生成不规则集料的基本步骤。

根据上文的假设，采用随机分布函数来描述平面的分布以及集料形状，生成任意形状多边形集料的步骤为：

① 获取集料形心所在位置在平面区域内的随机分布函数和集料尺寸的随机分布函数。

② 按照混合料级配在设定好的平面区域内随机产生圆盘单元，并把相应集料的物理参数赋予它们。

③ 获取圆盘单元的几何（形心和半径）与物理信息（密度、刚度等）。

④ 产生多边形集料，其算法按照以下方法进行：

a. 根据上文假设条件，假定混合料中的集料为多边形，而多边形的外接圆C 即为圆盘的外边界。

b. 随机产生一个大于3 的整数n，将其作为多边形的边数。

c. 在外接圆C 上根据随机产生的整数n 产生n 个点，并按顺序将各点连接起来形成一个封闭的多边形。

d. 用颗粒单元填充形成的多边形，将物理属性赋予形成多边形的颗粒单元。

⑤ 集料级配的检验与调整

多边形集料生成后，需要检验数值集料与实际集料级配的差异性，并进行调整：

a. 级配的检验：将每个级配范围内的多边形数值集料分离出来，并计算出各个级配数值集料的质量百分率。将此百分率与实际级配进行比较，确定生成级配是否满足条件。

b. 级配的调整：如果生成的级配满足要求则保留原级配不需要调整；否则，对生成级配进行相应的调整。