在大气边界层内，风速可分解为主方向的平均风速和3个互相垂直的脉动分量。定义x轴为平均风速的方向，y轴为水平方向，z轴为垂直方向，并且以向上为正，则在任意t时刻的风速可表示如下：

顺风向

U(z)+u(x,y,z,t)

横风向

v(x,y,z,t)

竖向

w(x,y,z,t)

式中　U——平均风速，取决于离地高度z；

u，v，w——风场各个垂直方向的脉动分量。

可定义U1（t），U2（t）和U3（t）分别为超声风速仪坐标下的3个实数序列。本次实测中，这3个方向分别为正北、正东和竖向3个方向。以10 min为基本时距进行分析，则三维超声风速仪的数学转换关系的详细推导如下：

超声风速记录仪的3个方向的10 min平均风速为

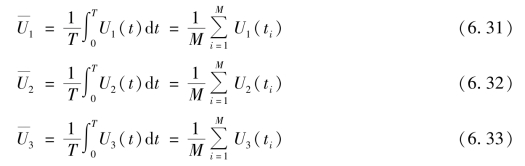
通过下式可得平均风速的数值，且可定义平均风速合成矢量U与u的正向为同一方向，即(www.daowen.com)

由于顺风向（主风向）脉动风速分量u的正向定义为与平均风速合成矢量为同一方向，因此，u（t）的正向通过平均风速的余弦向量（cos αu，cos βu，cos γu）定义如图6.9（a）所示。横向脉动风速分量v（t）垂直于平均风速U，而竖向脉动风速分量w（t）垂直于u（t）和v（t）。因此，横向脉动风速分量的方向余弦向量为向量（0，0，1）和向量（cos αu，cos βu，cos γu）的叉积，如图6.9（b）所示；竖向脉动风速分量的方向余弦（cos αw，cos βw，cos γw）是向量（cos αu，cos βu，cos γu）和（cos αv，cos βv，cos γv）的叉积，如图6.9（c）所示。由此可得3个来流风速方向对应的9个方向余弦，即

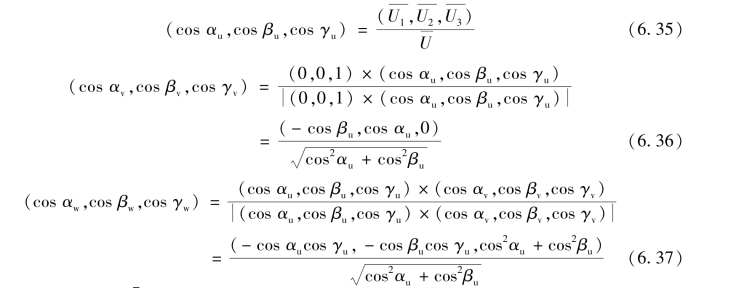
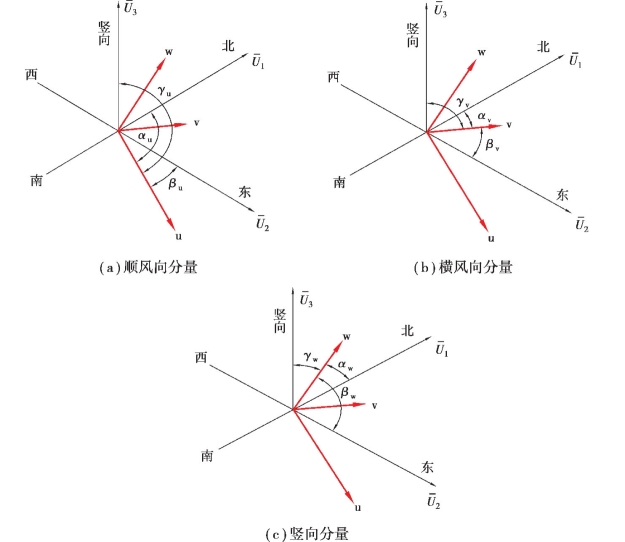
图6.9　脉动分量方向余弦定义

当求得三维风的9个方向余弦后，可得顺风向、横风向和竖向的脉动分量，即

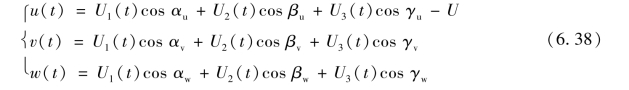
顺风向的分量总和U（t）可计算为

根据式（6.35）—式（6.39），以2013年11月17日15：00~16：00的60 min原始10 Hz数据为样本，采用Matlab进行脉动分量的分析，得到了桥位处实测风速时程的顺风向、横风向和竖向的脉动分量。如图6.10所示为3个方向的脉动风速时程。

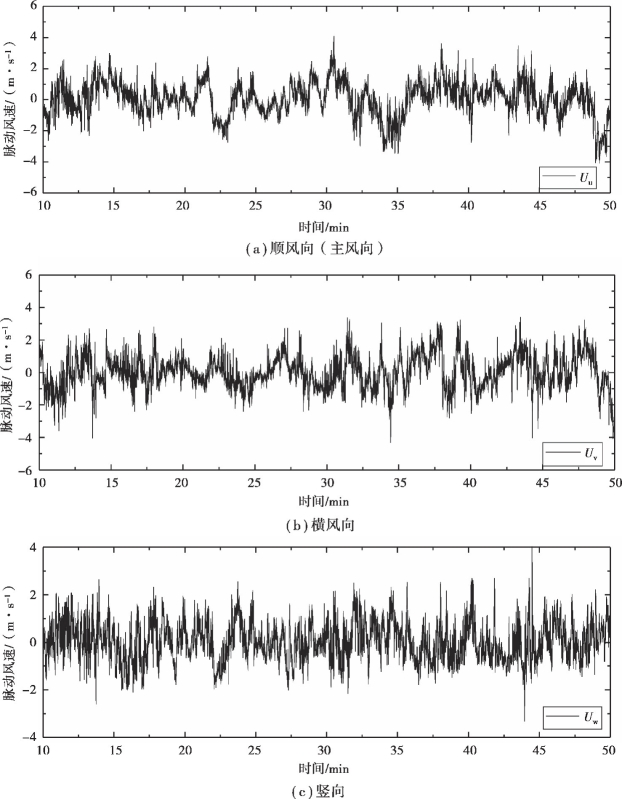
图6.10　脉动风速时程