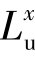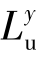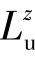紊流积分尺度是脉动风中湍流旋涡平均尺寸的度量，对应于纵向、横向和垂直方向脉动速度分量u，v，和w有关的3个方向，一共有9个紊流积分尺度，如，和分别度量与顺风向脉动风速有关的旋涡在纵向、横向和垂直方向的平均尺寸。在数学上可定义为

式中　R12（x）——两个不同空间位置上纵向脉动速度u1=u（x1，y1，z1，t）和u2=u（x2，y2，z2，t）的协方差函数，t为时间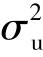；——脉动速度的方差。

同样的定义也可适用于其他方向的紊流积分尺度计算。

如果紊流旋涡以平均风速U进行迁移，则脉动速度u（x1，t+）可定义为x=Ut，这就是Taylor的“Frozen”假设。根据Taylor假设，式（6.2）可改为

式中　Ru（）——脉动风速u（x1，t+）的自相关函数，。

同理，可求得其他方向的紊流积分尺度。

直接应用式（6.2）计算积分尺度实际上是十分困难的。由于紊流积分尺度是与湍流空间相关性关联的参数，最理想的分析方法是在空间上实现多点同时测量，然后根据式（6.2）得到紊流积分尺度，然而遗憾的是空间多点同时测量往往较难实现。因此，实际风观测总是根据Taylor假设，将多点测量简化为单点测量。具体计算时，常用的计算方法有以下5种：

①根据式（6.2）直接用空间相关函数求积分尺度。

②用自相关函数代替空间相关函数，根据式（6.3）计算，当自相关系数很小时，Taylor假设引起的误差会增大，Flay等认为式（6.3）的积分上限取到为最佳[137]。(www.daowen.com)

③Davenport[138]建议空间相关函数应服从指数衰减律，那么根据Taylor假设，自相关函数也应服从指数衰减率。因此，式（6.3）又可改写为

式中　a——拟合的指数衰减系数。

④Reed和Scanlan采用自拟合模型（AR模型），将大气湍流作为理想的随机平稳过程处理，如此脉动速度可由一系列白噪声信号通过线性滤波系统产生，从而建立自拟合模型[139]。经比较确定合适的延迟时间和线性阶次，当平均风速大于10 m/s时，建议采用二阶线性滤波模型；当平均风速小于10.0 m/s时，一阶线性滤波模型较合适。

⑤若脉动风谱符合Karman谱，紊流积分尺度可从功率谱密度函数直接求出[140]，即

式中　Su（0）——对应脉动速度的功率谱在f=0的值；

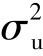——对应脉动速度的均方根；

np——对应脉动速度分量的功律谱密度函数峰值频率。

实际中，与纵向脉动速度有关的3个积分尺度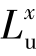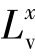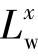，，基于Taylor假设得到相应的积分时间尺度进行计算[141]。庞加斌等的试验研究证实了泰勒假设的合理性[142]。在具体计算时，由于Taylor假设在自相关函数很小时，会引起较大的误差[142]。根据文献[137]，本书将积分上限取到，即自相关系数取为0.05~1.0。