5.2.2 矩形截面或翼缘位于受拉边的T形截面受弯构件,其正截面抗弯承载力计算应符合下列规定(图5.2.2):
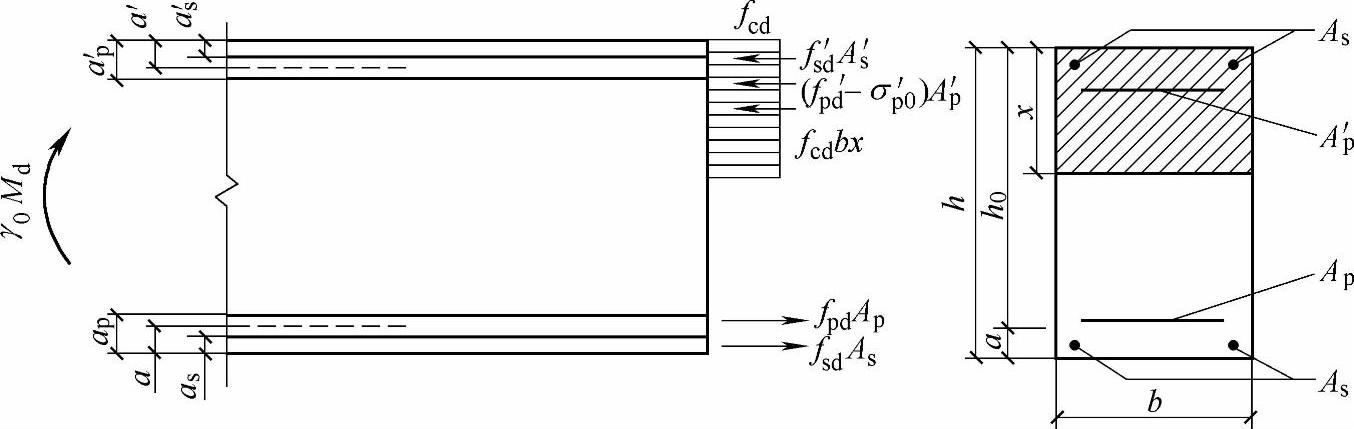
图5.2.2 矩形截面受弯构件正截面承载力计算
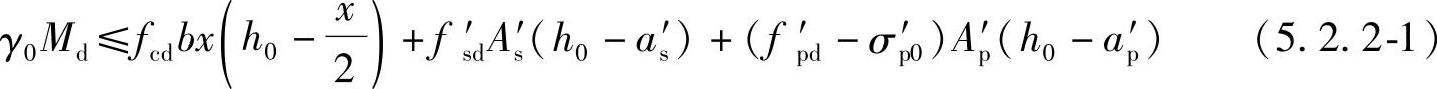
混凝土受压区高度x应按下式计算:
fsdAs+fpdAp=fcdbx+f′sdAs′+(f′pd-σ′p0)Ap′ (5.2.2-2)
截面受压区高度应符合下列要求:
x≤ξbh0 (5.2.2-3)
当受压区配有纵向普通钢筋和预应力钢筋,且预应力钢筋受压即(fp′d-σp′0)为正时
x≥2a′ (5.2.2-4)
当受压区仅配纵向普通钢筋或配普通钢筋和预应力钢筋,且预应力钢筋受拉即(f′pd-σp′0)为负时
x≥2as′ (5.2.2-5)
式中 γ0——桥梁结构的重要性系数,按本规范第5.1.5条的规定采用;
Md——弯矩组合设计值;
fcd——混凝土轴心抗压强度设计值,按本规范表3.1.4采用;
fsd、f′sd——纵向普通钢筋的抗拉强度设计值和抗压强度设计值,按本规范表3.2.3-1采用;
fpd、f′pd——纵向预应力钢筋的抗拉强度设计值和抗压强度设计值,按本规范表3.2.3-2采用;
As、As′——受拉区、受压区纵向普通钢筋的截面面积;
Ap、Ap′——受拉区、受压区纵向预应力钢筋的截面面积;
b——矩形截面宽度或T形截面腹板宽度;
h0——截面有效高度,h0=h-a,此处h为截面全高;
a、a′——受拉区、受压区普通钢筋和预应力钢筋的合力点至受拉区边缘、受压区边缘的距离;
as′、ap′——受压区普通钢筋合力点、预应力钢筋合力点至受压区边缘的距离;
σp0′——受压区预应力钢筋合力点处混凝土法向应力等于零时预应力钢筋的应力,先张法构件按本规范公式(6.1.5-2)计算;后张法构件按本规范公式(6.1.5-5)及第6.1.5条注2规定计算。
注:当桥梁为预应力混凝土连续梁等超静定结构时,公式(5.2.2-1)中的Md,应改用按本规范第
5.1.5条的规定进行作用(或荷载)效应组合。
5.2.1 受弯构件的纵向受拉钢筋和截面受压区混凝土同时达到其强度设计值时,构件的正截面相对界限受压区高度ξb应按表5.2.1采用。
表5.2.1 相对界限受压区高度ξb
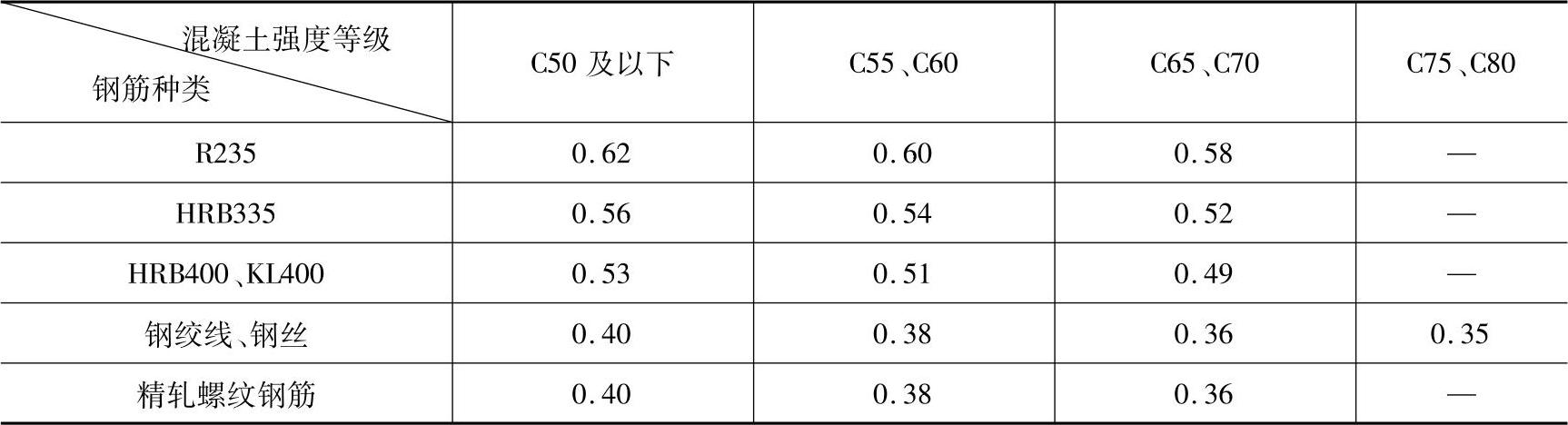
注:1.截面受拉区内配置不同种类钢筋的受弯构件,其ξb值应选用相应于各种钢筋的较小者;
2.ξb=xb/h0,xb为纵向受拉钢筋和受压区混凝土同时达到其强度设计值时的受压区高度。
9.1.12 钢筋混凝土构件中纵向受力钢筋的最小配筋百分率应符合下列要求:
2 受弯构件、偏心受拉构件及轴心受拉构件的一侧受拉钢筋的配筋百分率不应小于0.45ftd/fsd,同时不应小于0.002。
轴心受压构件、偏心受压构件全部纵向钢筋的配筋百分率和一侧纵向钢筋(包括大偏心受拉构件受压钢筋)的配筋百分率应按构件的毛截面面积计算。轴心受拉构件及小偏心受拉构件一侧受拉钢筋的配筋百分率应按构件毛截面面积计算。受弯构件、大偏心受拉构件的一侧受拉钢筋的配筋百分率为100As/bh0,其中As为受拉钢筋截面面积,b为腹板宽度(箱形截面梁为各腹板宽度之和),h0为有效高度。当钢筋沿构件截面周边布置时,“一侧的受压钢筋”或“一侧的受拉钢筋”系指受力方向两个对边中的一边布置的纵向钢筋。
(一)单筋矩形截面
【13.1.1】 单筋梁求As
条件:矩形截面尺寸b×h为250mm×500mm,承受的弯矩组合设计值Md=136kN·m,结构重要性系数γ0=1;采用C25混凝土,HRB335钢筋。
要求:所需钢筋截面面积As。
【解答】 根据采用的材料查得:fcd=11.5MPa,ftd=1.23MPa,fsd=280MPa,ξb=0.56。梁的有效高度h0=500-40=460mm(按布置一排钢筋估算)。
首先求解受压区高度x,即得
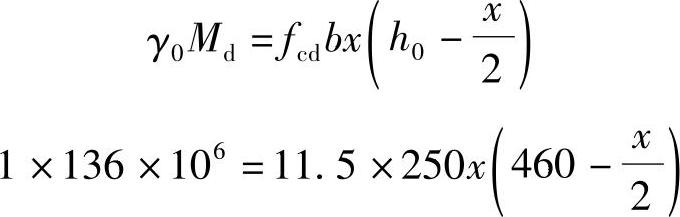
展开为x2-920x+94608.7=0
解得x=117.96mm<ξbh0=0.56×460=257.6mm。用所得的x值,即可求得所需钢筋截面面积为
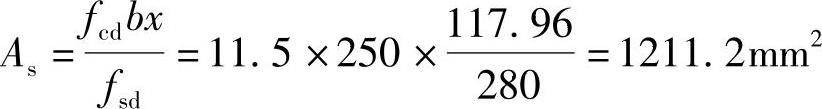
选取4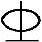 20(外径22.7mm)提供的钢筋截面面积As=1256mm2,钢筋按一排布置,所需截面最小宽度bmin=2×30+4×22.7+3×30=240.8mm<b=250mm,梁的实际有效高度h0=500-(30+22.7/2)=458.7mm,实际配筋率ρ=As/bh0=1256/250×458.7=0.01095>ρmin=0.45ftd/fsd=0.45×1.23/280=0.00197≈0.002。
20(外径22.7mm)提供的钢筋截面面积As=1256mm2,钢筋按一排布置,所需截面最小宽度bmin=2×30+4×22.7+3×30=240.8mm<b=250mm,梁的实际有效高度h0=500-(30+22.7/2)=458.7mm,实际配筋率ρ=As/bh0=1256/250×458.7=0.01095>ρmin=0.45ftd/fsd=0.45×1.23/280=0.00197≈0.002。
【13.1.2】 单筋梁的承载力复核
条件:已知一矩形截面梁,截面尺寸b=400mm,h=900mm,弯矩组合设计值Md=800kN·m,混凝土强度等级C30,钢筋等级为HRB335,As=4926mm2,as=60mm。
要求:复核正截面受弯承载力。
【解答】 查表得fcd=13.8MPa,fsd=280MPa,ξb=0.56。
(1)计算混凝土受压区高度
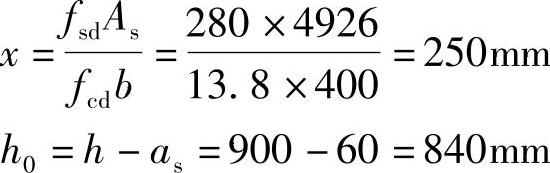
x=250mm<ξbh0=0.56×840=470.4mm,满足要求。
(2)计算截面所能承受的最大弯矩值,并做比较
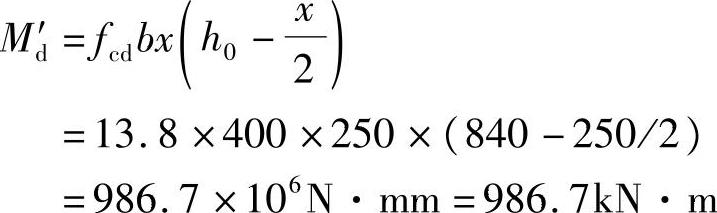
Md′>Md=800kN·m,结构安全。
(二)双筋矩形截面
《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定:
5.2.5 当计算中考虑受压区纵向钢筋但不符合本规范公式(5.2.2-4)、式(5.2.2-5)的条件时,受弯构件正截面抗弯承载力的计算应符合下列规定(图5.2.2):
1 当受压区配有纵向普通钢筋和预应力钢筋,且预应力钢筋受压时
γ0Md≤fpdAp(h-ap-a′)+fsdAs(h-as-a′) (5.2.5-1)
2 当受压区仅配纵向普通钢筋或配普通钢筋和预应力钢筋,且预应力钢筋受拉时
γ0Md≤fpdAp(h-ap-as′)+fsdAs(h-as-as′)-(fp′d-σ′p0)Ap′(ap′-as′) (5.2.5-2)
式中 as、ap——受拉区普通钢筋合力点、预应力钢筋合力点至受拉区边缘的距离。
【13.1.3】 双筋梁的截面设计
条件:有一截面尺寸为250mm×600mm的矩形截面梁,所承受的最大弯矩组合设计值Md=400kN·m,结构重要性系数γ0=1。拟采用C30混凝土、HRB400钢筋,fcd=13.8MPa,fsd=330MPa,f′sd=330MPa,ξb=0.53。
要求:试选择截面配筋,并复核正截面承载能力。
【解答】 假设as=70mm,as′=40mm,则h0=600-70=530mm。
首先,求xb=ξbh0=0.53×530=280.9mm的截面所能承受的最大弯矩组合设计值Mdb,
判断截面配筋类型
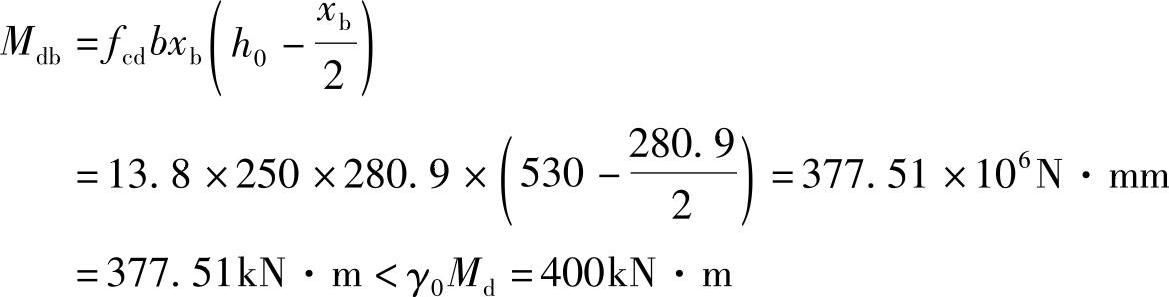
故应按双筋截面设计。
从充分利用混凝土抗压强度出发,取x=ξbh0=0.53×530=280.9mm,求得
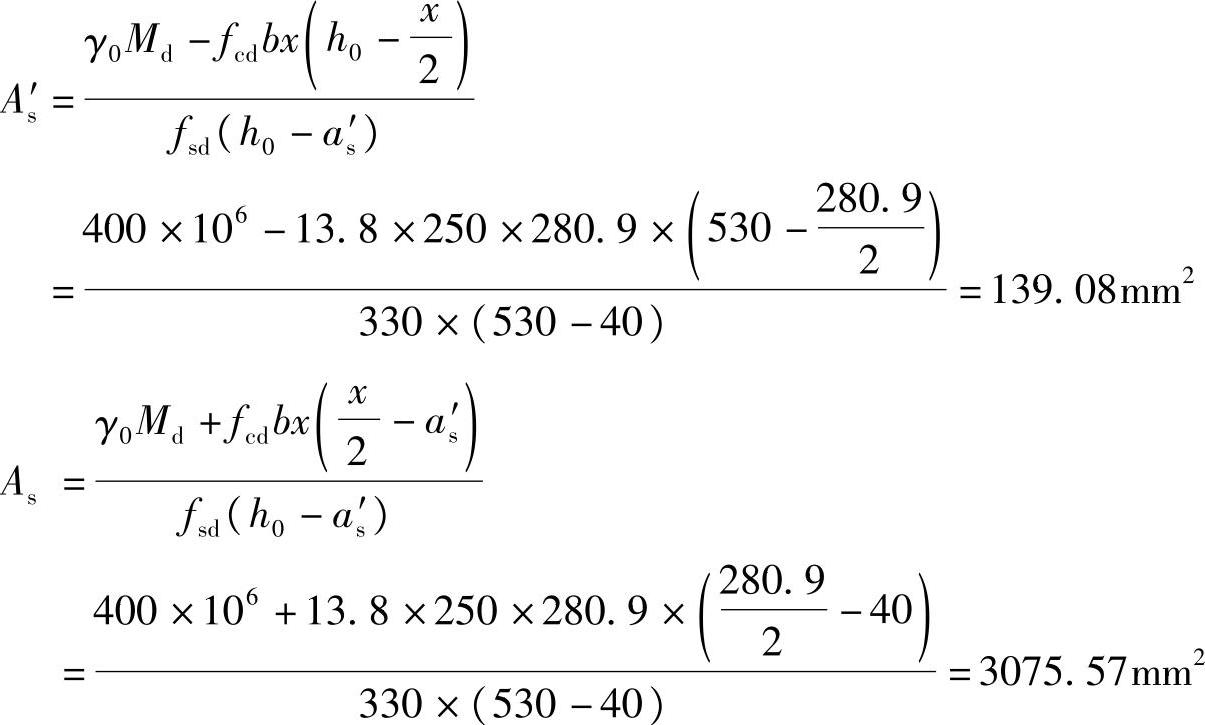
受压钢筋选2 12(外径13.9mm),面积As′=226mm2,αs′=30+13.9/2=37mm。
12(外径13.9mm),面积As′=226mm2,αs′=30+13.9/2=37mm。
受拉钢筋选8 22(外径25.1mm),面积As=3041mm2,布置成两排,所需截面最小宽度bmin=2×30+4×25.1+3×30=250mm=b=250mm,as=30+25.1+30/2=70.1mm,h0=600-70.1=529.9mm。
22(外径25.1mm),面积As=3041mm2,布置成两排,所需截面最小宽度bmin=2×30+4×25.1+3×30=250mm=b=250mm,as=30+25.1+30/2=70.1mm,h0=600-70.1=529.9mm。
按实际配筋情况复核截面承载能力。
此时,计算所得混凝土受压区高度为
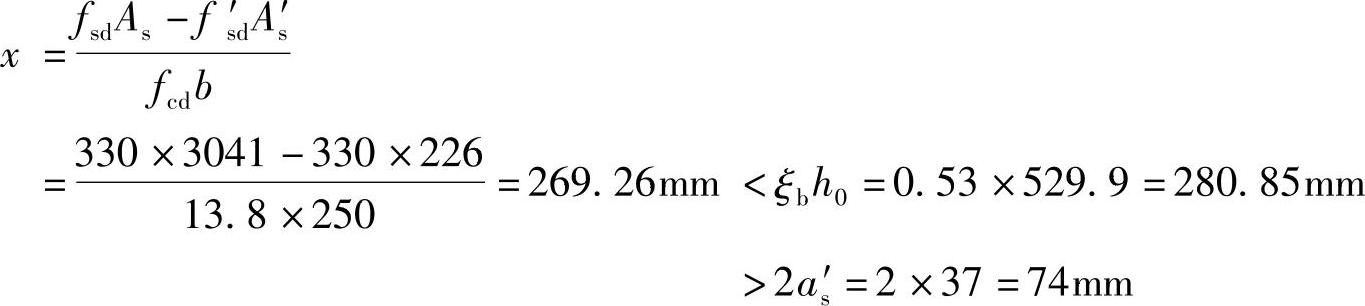
该截面所能承受的弯矩设计值为
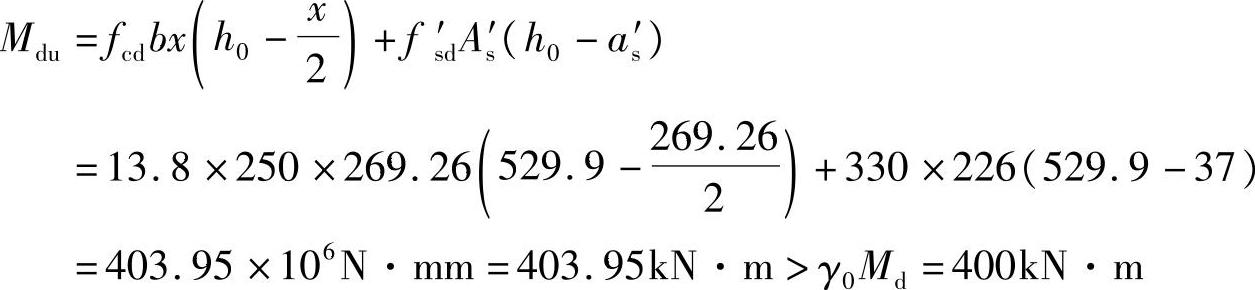
计算结果表明,截面承载力是够的。
(三)T形截面
《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定:
5.2.3 翼缘位于受压区的T形截面或I形截面受弯构件,其正截面抗弯承载力应按下列规定进行计算:
1 当符合下列条件时
fsdAs+fpdAp≤fcdbf′hf′+fs′dAs′+(fp′d-σp′0)Ap′ (5.2.3-1)
应以宽度为bf′的矩形截面(图5.2.3a),按本规范第5.2.2条公式计算正截面抗弯承载力。
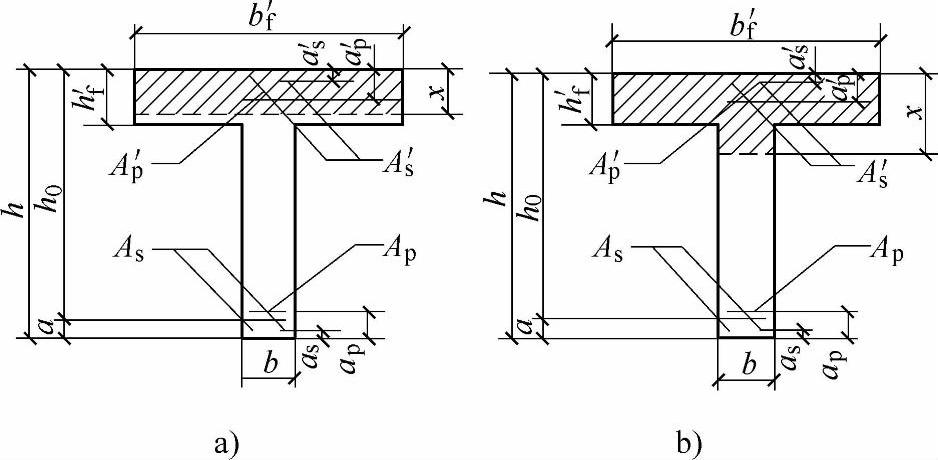
图5.2.3 T形截面受弯构件正截面承载力计算
a)x≤hf按矩形截面计算 b)x>hf按T形截面计算
2 当不符合公式(5.2.3-1)的条件时,计算中应考虑截面腹板受压的作用,其正截面抗弯承载力应按下列规定计算(图5.2.3b):
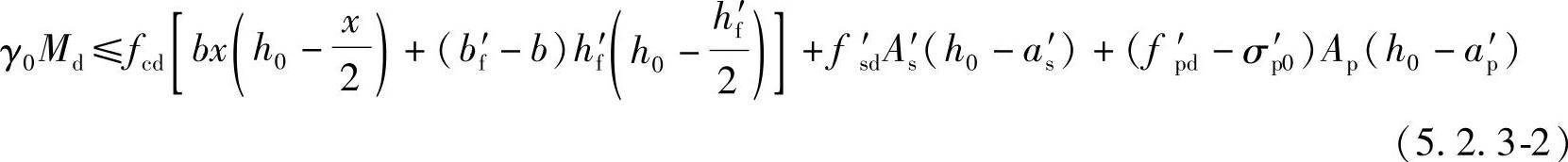
此时,受压区高度x应按下列公式计算,并应符合本规范公式(5.2.2-3)、式(5.2.2-4)、式(5.2.2-5)的要求。
fsdAs+fpdAp=fcd[bx+(bf′-b)hf′]+f′sdAs′+(fp′d-σ′p0)Ap′ (5.2.3-3)
式中 hf′——T形或I形截面受压翼缘厚度;
bf′——T形或I形截面受压翼缘的有效宽度,按本规范第4.2.2条的规定采用。箱形截面受弯构件的正截面抗弯承载力可参照本条计算。
注:图5.2.3截面内力作用方向与本规范图5.2.2相同。
4.2.2 T形截面梁的翼缘有效宽度bf′,应按下列规定采用:
1 内梁的翼缘有效宽度取下列三者中的最小值:(www.daowen.com)
1)对于简支梁,取计算跨径的1/3。对于连续梁,各中间跨正弯矩区段,取该计算跨径的0.2倍;边跨正弯矩区段,取该跨计算跨径的0.27倍;各中间支点负弯矩区段,取该支点相邻两计算跨径之和的0.07倍;
2)相邻两梁的平均间距;
3)(b+2bh+12hf′),此处,b为梁腹板宽度,bh为承托长度,hf′为受压区翼缘悬出板的厚度。当hh/bh<1/3时,上式bh应以3hb代替,此处hh为承托根部厚度。
2 外梁翼缘的有效宽度取相邻内梁翼缘有效宽度的一半,加上腹板宽度的1/2,再加上外侧悬臂板平均厚度的6倍或外侧悬臂板实际宽度两者中的较小者。
预应力混凝土梁在计算预加力引起的混凝土应力时,预加力作为轴向力产生的应力可按实际翼缘全宽计算;由预加力偏心引起的弯矩产生的应力可按翼缘有效宽度计算。
对超静定结构进行作用(或荷载)效应分析时,T形截面梁的翼缘宽度可取实际全宽。
【13.1.4】 T形截面梁的截面设计(x<hf′)
条件:已知简支梁的计算跨径L=12.6m,两主梁中心距为2.1m,其截面尺寸如图13.1.1所示。混凝土为C30,HRB400级钢筋,桥梁结构的重要性系数γ0=1.0,所承受的弯矩组合设计值Md=2800kN·m。
要求:试设计配筋。
【解答】
(1)确定翼缘板计算宽度bf′。
1)简支梁计算跨径的1/3为:12600/3=4200mm。
2)主梁中心距为2100mm。
3)b+12hf′=400+12×130=1960mm。
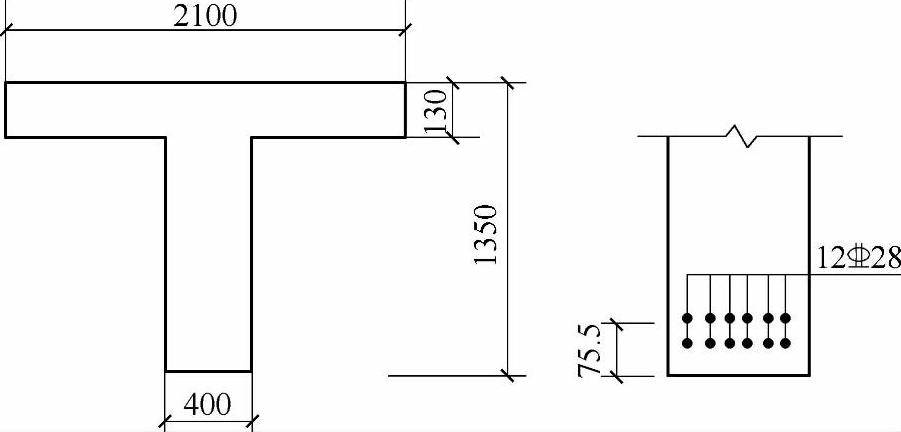
图13.1.1 截面尺寸图(尺寸单位:mm)
所以,取翼缘板的计算宽度bf′=1960mm。
(2)判断T形截面类型。查表得fcd=13.8MPa,fsd=330MPa,ftd=1.39MPa,ξb=0.53,假定受拉钢筋布置成两排,取as=70mm,h0=h-as=1350-70=1280mm,先判断截面类型,当x=hf′时,截面所能承受的弯矩设计值为
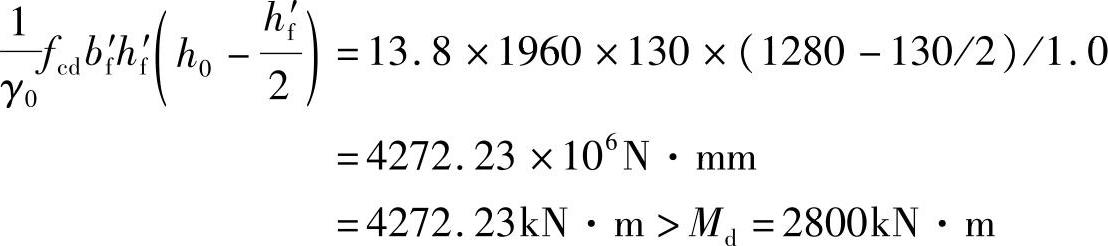
因中性轴在翼缘内,属于第Ⅰ类T形截面梁,应按bf′h=1960mm×1350mm的矩形截面进行计算。
(3)计算混凝土受压区高度x
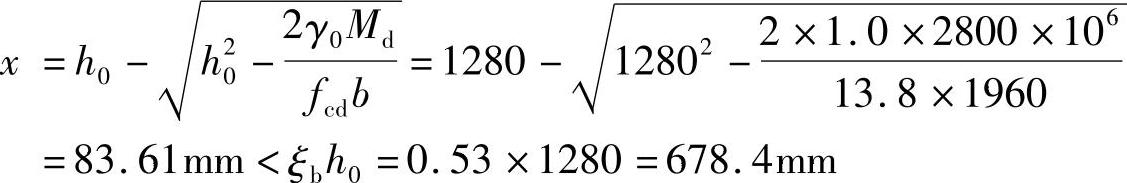
且x<hf′=130mm
求得所需受拉钢筋截面面积为
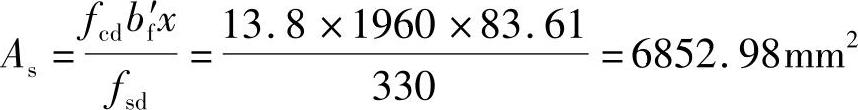
选12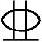 28(外径30.5mm),提供的钢筋截面面积As=7388.4mm2,12根钢筋布置成两排,每排6根,所需截面最小宽度bmin=2×25+5×30+6×30.5=383mm<b=400mm,受拉钢筋合力作用点至梁下边缘的距离
28(外径30.5mm),提供的钢筋截面面积As=7388.4mm2,12根钢筋布置成两排,每排6根,所需截面最小宽度bmin=2×25+5×30+6×30.5=383mm<b=400mm,受拉钢筋合力作用点至梁下边缘的距离
as=30+30.5+30/2=75.5mm
h0=h-as=1350-75.5=1274.5mm
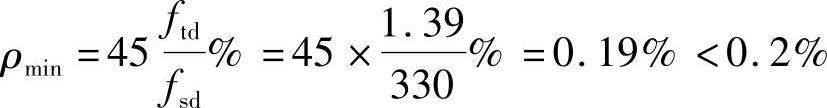 ,取ρmin=0.2%
,取ρmin=0.2%
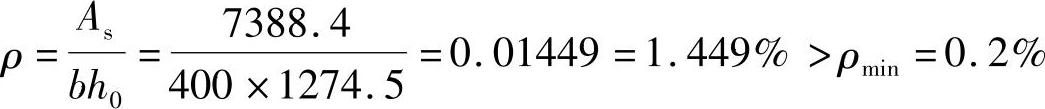
【13.1.5】 T形截面梁的截面设计(x>hf′)
条件:T形截面梁截面尺寸如图13.1.2所示,所承受的弯矩组合设计值Md=580kN·m,结构重要性系数γ0=1.0。拟采用C30混凝土,HRB400钢筋,fcd=13.8MPa,ftd=1.39MPa,fsd=330MPa,ξb=0.53。
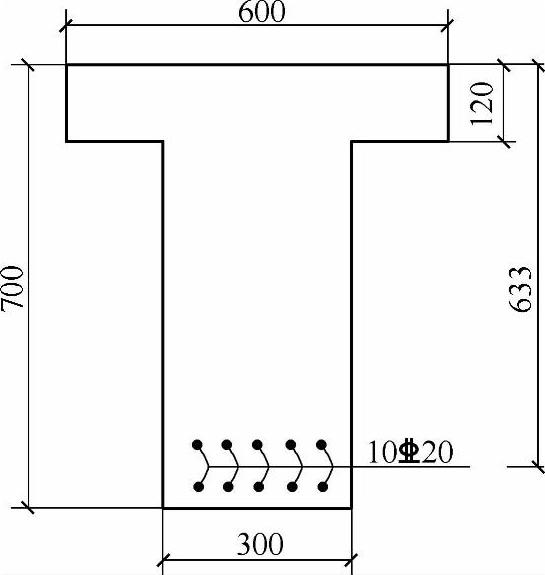
图13.1.2 T形梁截面尺寸及配筋(尺寸单位:mm)
要求:试选择钢筋,并复核正截面承载能力。
【解答】 按受拉钢筋布置成两排估算as=70mm,梁的有效高度h0=700-70=630mm。梁的翼缘有效宽度bf′=b+12h′f=300+12×120=1740mm>600mm,故取b′f=600mm。
首先判断截面类型,当x=hf′时,截面所能承受的弯矩设计值为
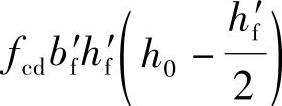
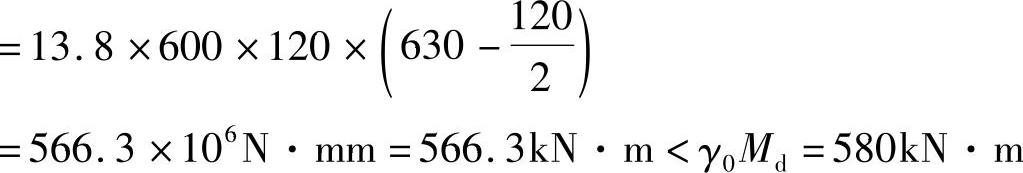
故应按x>hf′的T形截面计算。
令As′=0求得混凝土受压区高度x,即
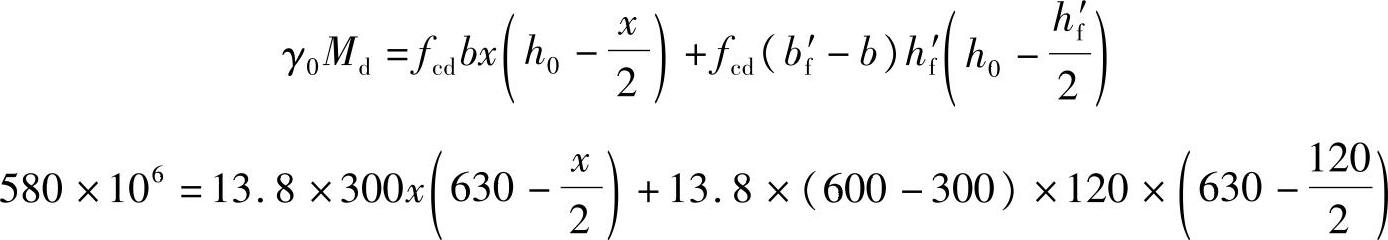
展开整理后得
x2-1260x+143393.23=0
解得:x=126.5mm>hf′=120mm
<ξbh0=0.53×630=333.9mm
由所得x求得
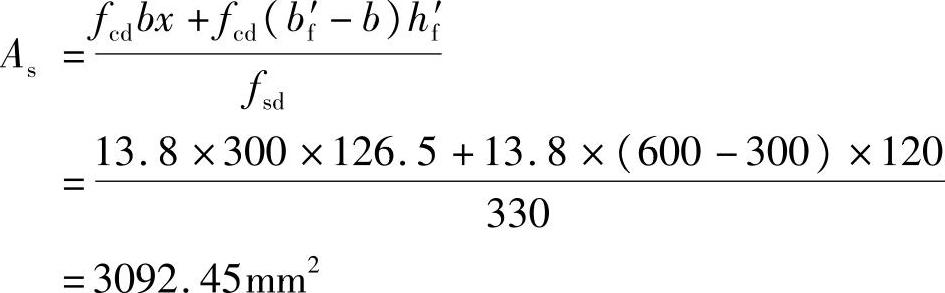
选择10真题20(外径22.7mm),钢筋截面面积As=3142mm2,10根钢筋布置成两排,每排5根,所需截面最小宽度bmin=2×30+5×22.7+4×30=293.5mm<b=300mm,受拉钢筋合力作用点至梁下边缘的距离as=30+22.7+30/2=67.7mm,梁的实际有效高度h0=700-67.7=632.3mm。
对上述已设计好截面进行承载能力复核时,按梁的实际配筋情况,再计算混凝土受压区高度x,即得
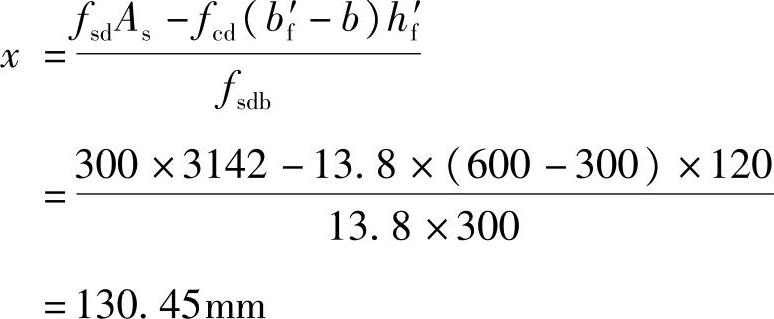
hf′=120mm<x=130.45mm<ξbh0=0.53×632.3=335.1mm
该截面所能承受的弯矩设计值为
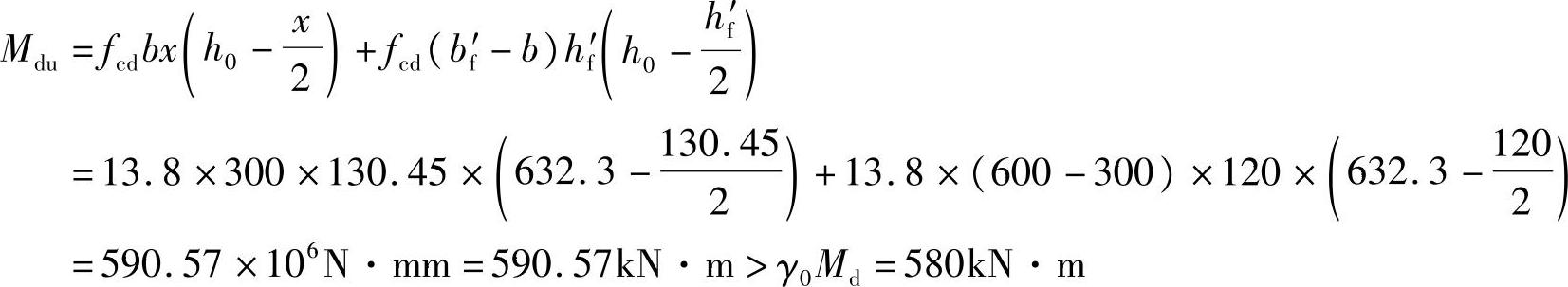
计算结果表明,该截面的抗弯承载力是足够的,结构是安全的。
真题 【13.1.6】 (2001年考题,因《规范》改版,故本题有关参数跟着作了相应调整)
某公路钢筋混凝土简支梁桥,其计算跨径L=14.5m,主梁由多片T形截面梁组成,其中单片主梁断面尺寸如图13.1.3所示,h0=67.5cm。采用混凝土C40,fcd=13.8MPa,主筋为HPB400级钢筋,fsd=330MPa。假定不计受压钢筋面积,并假定计算跨中弯矩M恒=1631.40kN·m,M活=289.30kN·m。试确定按承载能力极限状态计算出的跨中截面钢筋面积与下列何项数值最为接近?
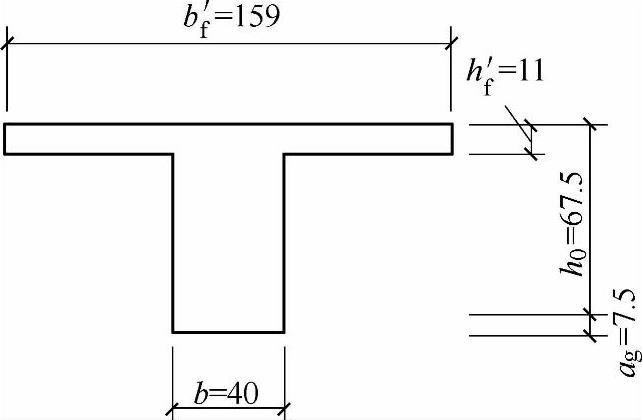
图13.1.3 主梁断面尺寸(单位:cm)
(A)71.88cm2 (B)64.62cm2
(C)53.23cm2 (D)49.47cm2
【答案】 (D)
【详解】
(1)根据《公路桥涵设计通用规范》表1.0.11,15m简支梁桥属小桥。
(2)根据《公路桥涵设计通用规范》表1.0.9,小桥的安全等级为三级。
(3)根据《公路桥涵设计通用规范》4.1.6条,设计安全等级三级的结构重要性系数γ0=0.9。
(4)确定荷载效应组合。根据《公路桥涵设计通用规范》4.1.6条,承载能力极限状态下的荷载效应组合为
Md=γGM恒+γQM活=1.2M恒+1.4M活
=1.2×1631.40+1.4×289.30=1162.7kN·m
式中,永久作用效应分项系数γG=1.2;
汽车荷载效应分项系数γQ=1.4。
(5)确定翼缘板计算宽度b′f。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》4.2.2条:
1)简支梁计算跨径的L/3为:14500/3=4834mm。
2)主梁中心距为1590mm。
3)b+12hf′=400+12×110=1720mm。
所以,取翼缘板的计算宽度bf′=1590mm。
(6)判断T形截面类型
已知:fcd=13.8MPa,ftd=1.39MPa,fsd=330MPa,h0=675mm,先判断截面类型,当x=hf′时,截面所能承受的弯矩设计值为
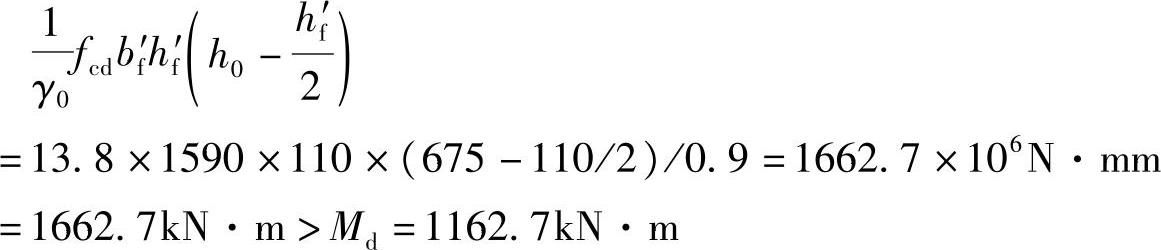
因中性轴在翼缘内,属于第Ⅰ类T形截面梁,应按b×h=1590mm×750mm的矩形截面进行计算。
(7)计算混凝土受压区高度x。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》5.2.2条
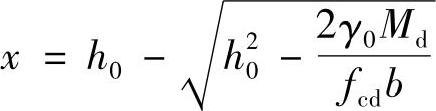
将Md=1162.7kN·m,h0=675mm,b=1590mm,fcd=13.8MPa代入上式
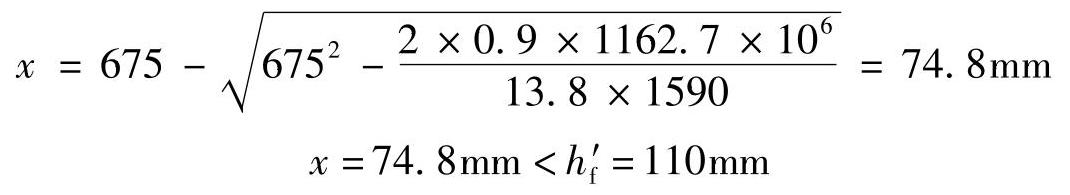
(8)求所需受拉钢筋截面面积为
根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》5.2.2条:
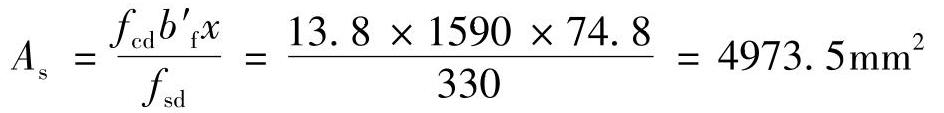
选8 28(外径30.5mm),提供的钢筋截面面积As=4926mm2。
28(外径30.5mm),提供的钢筋截面面积As=4926mm2。
(9)验算最小配筋率。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》5.2.12条,ftd=1.39MPa,fsd=330MPa
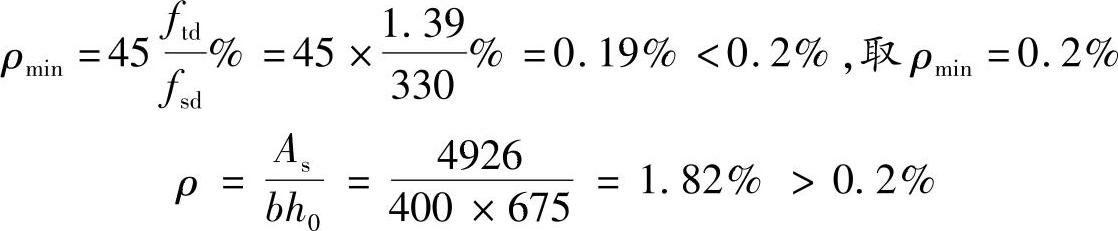
(10)确定跨中截面的钢筋面积As=4974mm2=49.74cm2,(D)正确。
【简解】
(1)根据《规范》4.1.6条,γ0=0.9
(2)Md=γGM恒+γQM活=1.2M恒+1.4M活=1.2×1631.40+1.4×289.30=1162.7kN·m
(3)取bf′=1590mm
(4) 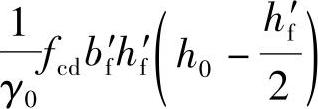
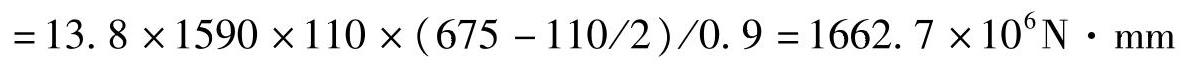
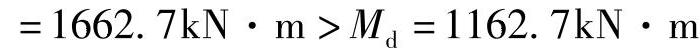 ,第Ⅰ类T形截面梁。
,第Ⅰ类T形截面梁。
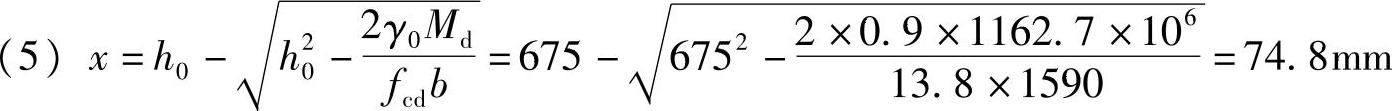
(6)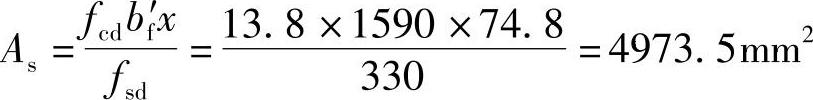 ,(D)正确。
,(D)正确。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






