T形、箱形截面受弯构件，在荷载作用下，由于上、下翼板的剪切变形使翼板中弯曲正应力呈不均匀分布现象，称之为剪力滞效应。远离腹板处的弯曲正应力小于腹板处的弯曲正应力，称之为正剪力滞效应；反之，称之为负剪力滞效应，如图11.3.7所示。

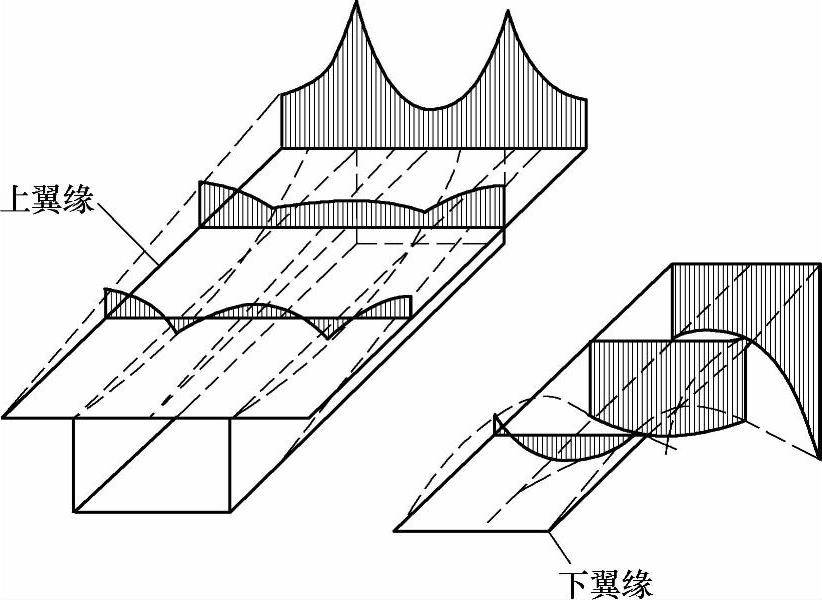
图 11.3.7

在梁的某一横断面上，翼板中某处弯曲正应力σ_y与按简支梁计算的该横断面的弯曲正应力σ₀之比为λ_y=σ_y/σ₀，λ_y定义为剪力滞系数。在该横断面上λ_y最大值大于1，最小值小于1。

分析剪力滞的常用方法——“翼缘有效宽度”法。

“翼缘有效宽度”法，即将实际的翼缘宽度按某种规律折减为计算宽度，再将梁的内力按材料力学理论算得应力，使该应力接近实际的应力峰值。需注意在计算超静定内力时可仍取原翼缘宽度，以简化计算。

《公路钢筋混凝土及预应力混凝土桥涵设计规范》中对箱形截面受弯构件受压区翼缘计算宽度规定：

4.2.3 箱形截面梁在腹板两侧上、下翼缘的有效宽度b_mi可按下列规定计算（图4.2.3-1、图4.2.3-2和表4.2.3）：

1 简支梁和连续梁各跨中部梁段，悬臂梁中间跨的中部梁段

b_mi=ρ_fb_i （4.2.3-1）

2 简支梁支点，连续梁边支点及中间支点，悬臂梁悬臂段

b_mi=ρ_sb_i （4.2.3-2）

式中 b_mi——腹板两侧上、下各翼缘的有效宽度，i=1，2，3…见图4.2.3-1；

b_i——腹板两侧上、下各翼缘的实际宽度，i=1，2，3…见图4.2.3-1；

ρ_f——有关简支梁、连续梁各跨中部梁段和悬臂梁中间跨的中部梁段翼缘有效宽度的计算系数，可按图4.2.3-2和表4.2.3确定；

ρ_s——有关简支梁支点、连续梁边支点和中间支点、悬臂梁悬臂段翼缘有效宽度的计算系数，可按图4.2.3-2和表4.2.3的确定。

注：（1）b_mi，f为简支梁和连续梁各跨中部梁段、悬臂梁中间跨的中部梁段，当b_i/l_i≥0.7时翼缘的有效宽度；

（2）b_mi，s为简支梁支点、连续梁边支点和中间支点、悬臂梁悬臂段，当b_i/l_i≥0.7时翼缘的有效宽度；

（3）l_i按表4.2.3确定。

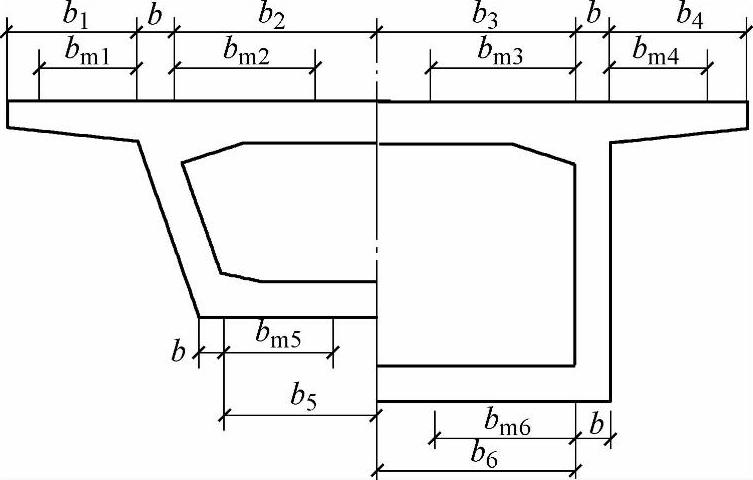
图4.2.3-1 箱形截面梁翼缘有效宽度

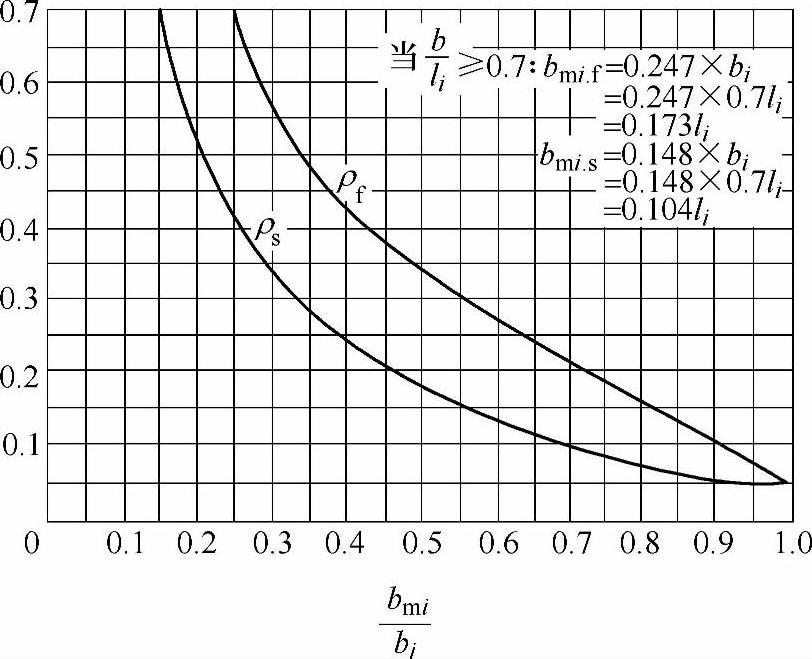
图4.2.3-2 ρ_s，ρ_t曲线图

表4.2.3 ρ_s、ρ_f的应用位置和理论跨径l_i

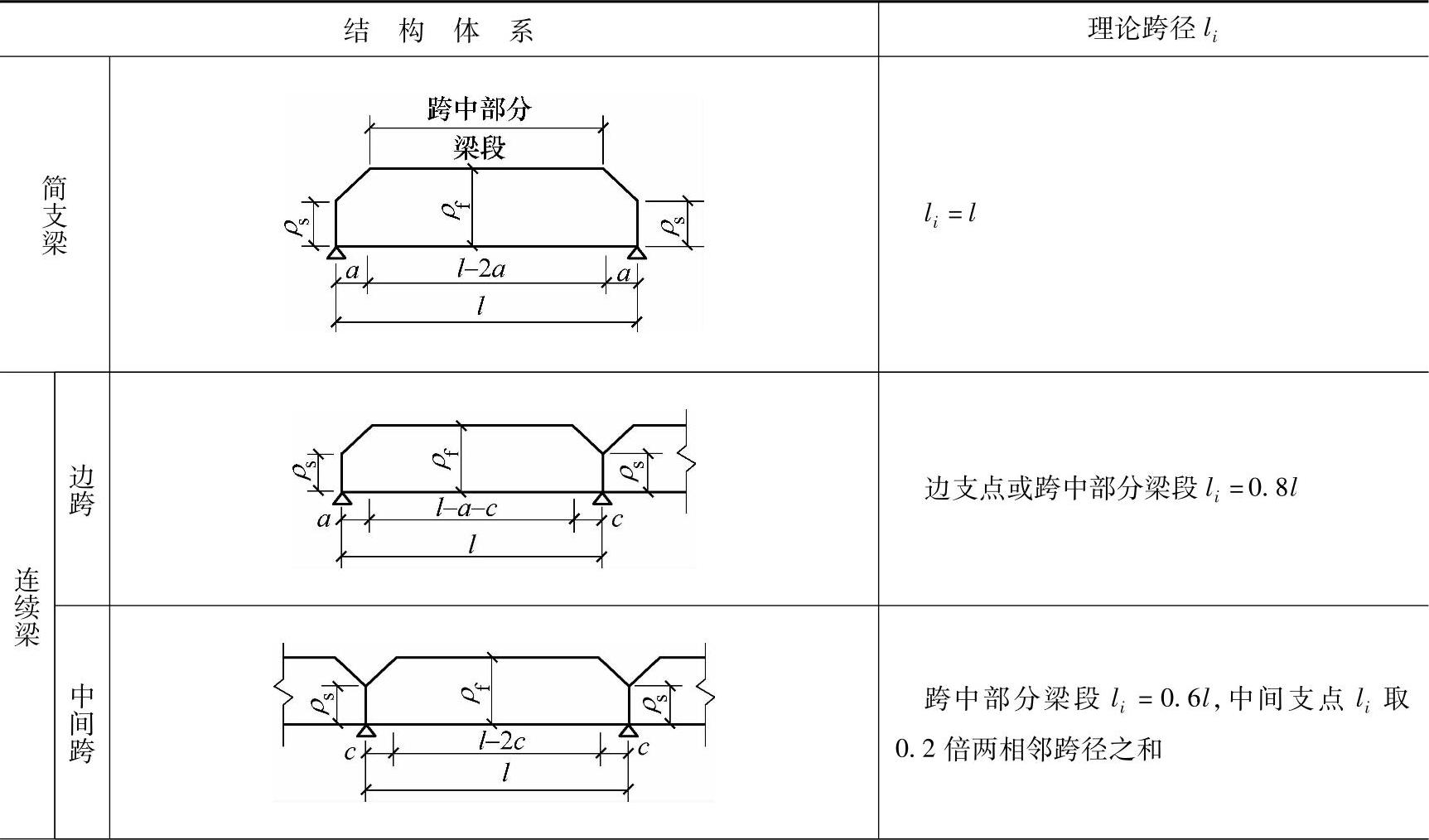
（续）(www.daowen.com)

注：（1）a为与所求的翼缘有效宽度b_mi相应的翼缘实际宽度b_i，但a不应大于0.25l；

（2）l为梁的计算跨径；

（3）c=0.1l；

（4）在长度a或c的梁段内，有效宽度可用直线插入法在ρ_sb_i与ρ_fb_i之间求取。

当梁高h≥b_i/0.3时，翼缘有效宽度应采用翼缘实际宽度。

预应力混凝土梁在计算预加力引起的混凝土应力时，预加力作为轴向力产生的应力可按实际翼缘全宽计算；由预加力偏心引起的弯矩产生的应力可按翼缘有效宽度计算。

对超静定结构进行作用（或荷载）效应分析时，箱形截面梁的翼缘宽度可取实际全宽。

【11.3.4】 计算箱形截面梁的翼缘有效宽度

条件：三跨等高度箱形截面混凝土连续梁，跨径组成及横截面尺寸如图11.3.8所示。

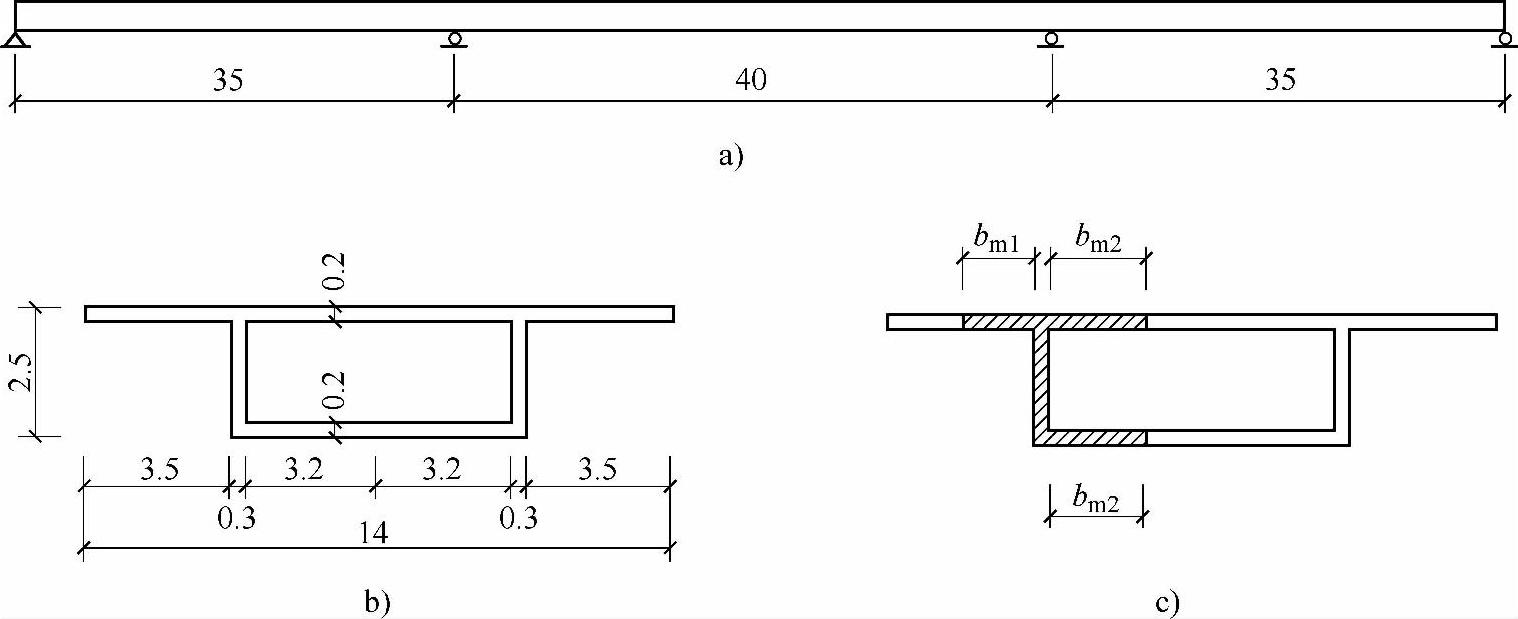
图11.3.8 跨径组成及横截面

a）梁桥跨径组成（m） b）梁跨横截面（m） c）翼缘有效宽度

要求：计算中间支点处的腹板两侧翼缘有效宽度b_m1、b_m2。

【解答】

（1）根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》4.2.3条规定，中支点截面位置处的理论跨径：

l=0.2（l_s+l_m）=0.2（35+40）=15m

（2）中支点截面位置处的翼缘实际宽度与理论跨径之比b_i/l_i。

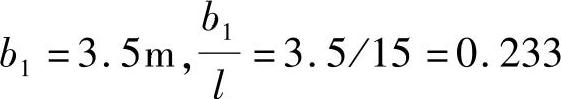
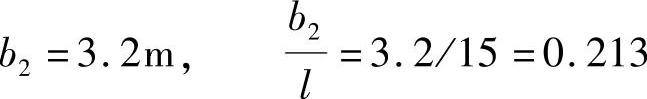
（3）根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》图4.2.3-2，查得ρ_s，按《公路钢筋混凝土及预应力混凝土桥涵设计规范》式（4.2.3-2）计算b_mi。

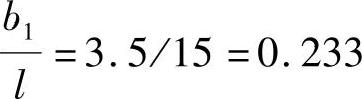，查得ρ_s=0.42，b_m1=0.42×3.5=1.47m

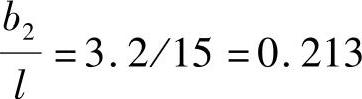，查得ρ_s=0.45，b_m2=0.45×3.2=1.44m

中间支点处的腹板两侧翼缘有效宽度b_m1=1.47m，b_m2=1.44m。