箱形截面梁的抗扭性能远远高于工字形截面梁，下面以同样的外形尺寸的工字形截面和箱形截面的受力特性进行比较，如图11.3.2所示。在竖向荷载作用下，因为它们的截面抗弯惯矩相等，所以它们的抗弯能力是相同的。但如果梁上作用的竖向荷载与截面中心有偏心，梁将受到扭转，这时两种截面的抗扭性能将表现出很大的差异。
如图11.3.2中取b=d/2，t=δ/2及δ=d/20，用材料力学理论计算其应力，那么工字形截面和箱形截面的剪应力见表11.3.1。
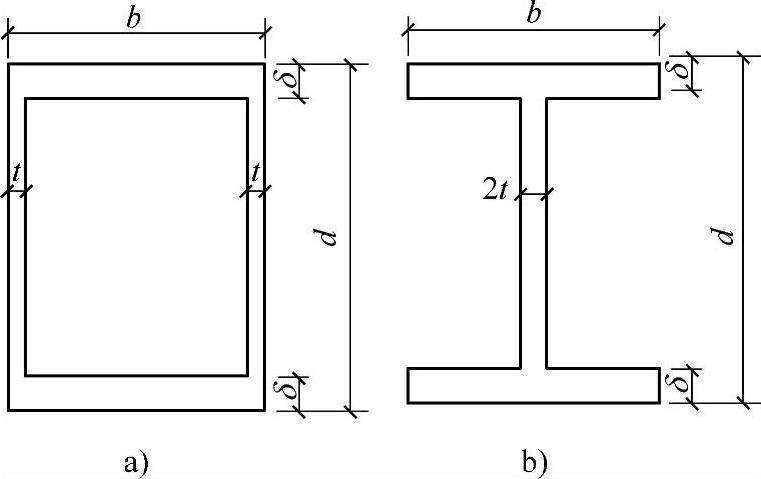
图11.3.2 工字形截面和箱形截面
表11.3.1 工字形截面与箱形截面抗扭能力比较
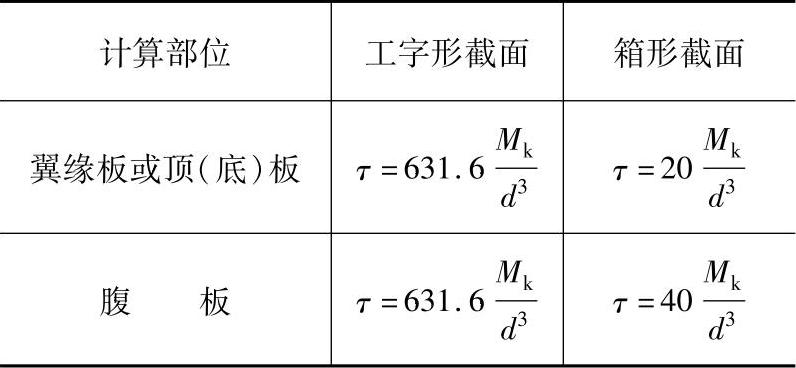
因此，以剪应力控制设计时，上述工字形截面和箱形截面所能承受的最大扭矩分别为
Mk（工）=τd3/631.6
Mk（箱）=τd3/40
两者的比值是Mk（箱）=15.79Mk（工）
即在同样的外形尺寸下，箱形截面所能承受的最大扭矩是工字形截面的15.79倍。这表明箱形截面具有很好的抵抗扭矩的能力。
下面进一步来分析箱形截面梁的受力特性。
作用于箱形截面梁的恒荷载一般是对称的，活荷载可以是对称，也可以是非对称的。箱形截面梁在偏心荷载作用下，可能产生弯曲、扭转、畸变及横向挠曲四种基本变形状态。
其中纵向弯曲和扭转主要计算纵向应力，局部横向弯曲主要计算横向应力，畸变则对两者都要计算。
对称纵向弯曲产生竖向变位，在横截面上引起纵向正应力σM及剪应力τM，如图11.3.3a所示。箱梁肋距不大时，可用材料力学理论计算其应力分布（图中虚线所示），当肋距较大时，需计入“剪力滞效应”，考虑其应力不均匀分布。
箱形截面梁的刚性扭转分为自由扭转和约束扭转，自由扭转不产生纵向正应力，只产生自由扭转剪应力τk，约束扭转将产生翘曲正应力σy和约束扭转剪应力τw，如图11.3.3b所示。箱形截面梁扭转的主要变形特征是扭转角θ。
畸变（即受扭时截面周边变形）的主要变形特征是畸变角γ。薄壁宽箱的矩形截面受扭后无法保持其截面投影仍为原截面，因而产生畸变翘曲正应力σdw和畸变剪应力τdw。同时，由于畸变而引起箱形截面各板横向弯曲在板内产生横向弯曲应力σdt，如图11.3.3c所示。
箱形截面梁承受顶板上荷载作用，在纵截面上产生横向弯曲正应力σc。
偏心荷载作用下箱形截面梁产生以下应力：
在横断面上：纵向正应力 σ=σM+σw+σdw （11.3.1）
剪应力 τ=τk+τM+τw+τdw （11.3.2）
在纵断面上：横向弯曲正应力 σs=σdt+τc （11.3.3）
在中等跨径以上的预应力混凝土连续梁中，多采用箱形横断面。跨径越大，恒荷载占总荷载的比例越大，悬臂施工时，施工期间荷载常常控制设计，因而对称弯曲正应力是主要的，活荷载偏心所产生的扭转应力是次要的。
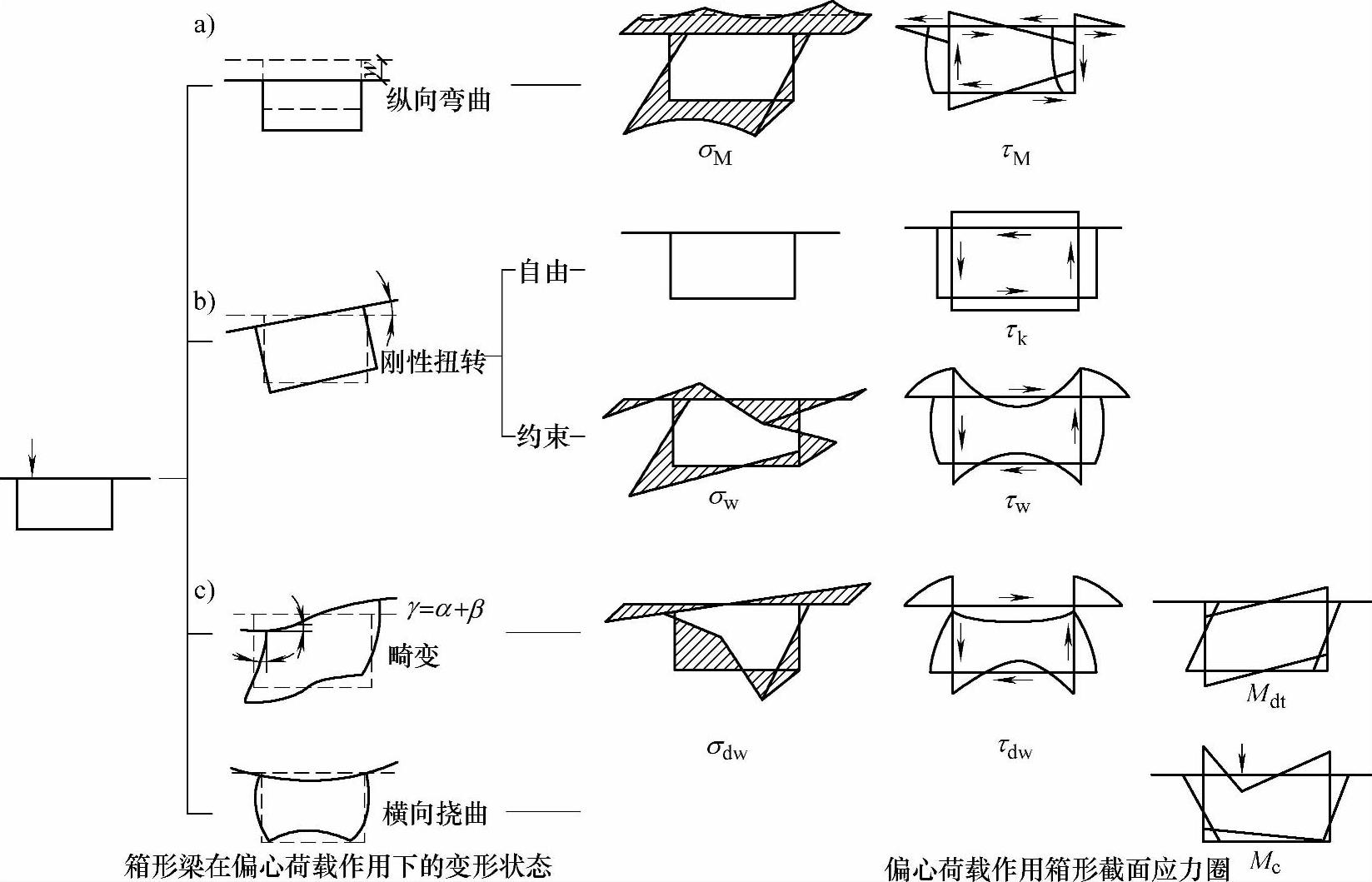
图11.3.3 箱梁在偏心荷载作用下的变形和应力图
对于箱壁较厚，或沿梁的纵向布置有一定数量的横隔板，限制箱梁的畸变，只需计算：①纵向弯曲应力；②刚性扭转应力。对于少设或不设横隔板的宽箱薄壁梁，还需计算：①畸变应力；②横向弯曲应力。
当桥面上作用偏心荷载时，整体箱形截面梁的受力可以分为两种情况进行分析：对称荷载作用下的平面弯曲问题和偏转作用下的扭转问题，对于平面弯曲问题，采用一般的材料力学公式就可以计算出横截面上的弯曲正应力和弯曲剪应力；对于扭转问题，计算内容较多，计算也较复杂。
普通钢筋混凝土和预应力钢筋混凝土箱形截面的抗扭刚度很大，由扭转引起的应力一般比平面弯曲引起的应力小得多。从简化计算的目的出发，可以采用先按纯弯构件计算出箱形截面梁的内力，在此基础上再考虑扭转的影响，即在纯弯内力上乘一个增大系数——扭转影响对箱形截面梁内力的不均匀系数k，这是一种偏保守的简化计算方法。例如图11.3.4所示的单箱三室截面，可以近似地把该结构视做用刚性横梁连接的四榀T字梁，采用偏心压力法求解各根主梁的横向分布系数mi。偏载时边梁受力最大，一般情况下，边主梁具有最大的mmax。为简化起见，假定每根主梁的横向分布系数均达到了mmax，考虑到箱形截面梁一般是按全截面来分析其内力，本例截面共由四根主梁组成（n=4），若每根主梁都承担同样大小的荷载，则应将mmax乘以n，便得到所谓的扭转影响对箱形截面梁内力的不均匀系数k。k=mmaxn亦称活载内力增大系数，常用的数值为1.0～1.2，如单箱单室可取k=1.0，单箱双室可取k=1.2。
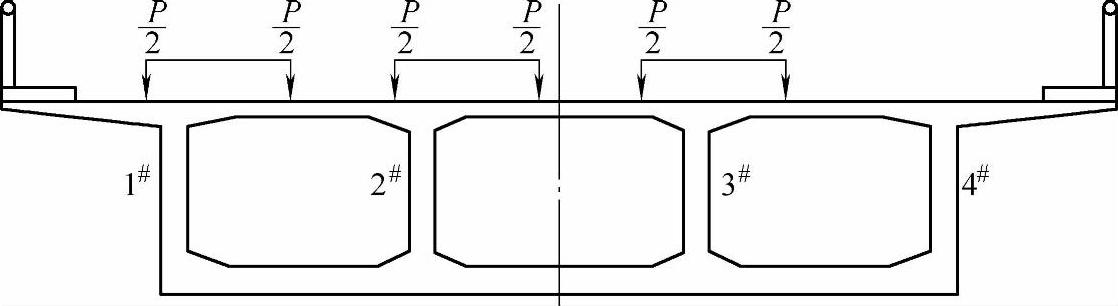
图11.3.4 扭转影响对箱形梁内力的不均匀系数
箱形梁（按全截面计算）其内力计算的一般公式为
S=（1+μ）ξK（qkΩ+Pkyp） （11.3.4）
1+μ——考虑冲击影响的增大系数；
ξ——汽车荷载横向折减系数；
K——扭转影响对箱形截面梁内力的不均匀系数（活荷载内力增大系数）；
qk——车道荷载的均布荷载标准值；
Ω——弯矩或剪力影响线的面积；
Pk——车道荷载的集中荷载标准值；
yp——对应于车道集中荷载的影响线最大竖标值。
真题 【11.3.1】 （2006年考题）
某一级公路设计行车速度V=100km/h，双向六车道，汽车荷载采用公路-Ⅰ级。其公路上有一座计算跨径为40m的预应力混凝土箱形截面简支梁桥，采用上、下双幅分离式横断面行驶。横断面布置如图11.3.5所示。计算该箱形截面梁桥汽车车道荷载时，应按横桥向偏载考虑。假定车道荷载冲击系数μ=0.215，车道横向折减系数为0.67，扭转影响对箱形截面梁内力的不均匀系数K=1.2，试问，该箱形截面梁桥跨中断面，由汽车车道荷载产生的弯矩作用标准值（kN·m），应与下列何项数值最为接近？
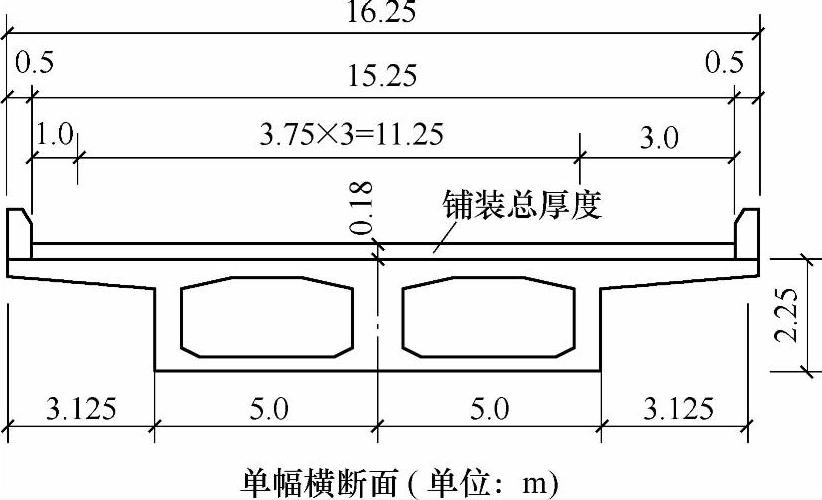
图 11.3.5
（A）21000 （B）21500 （C）22000 （D）22500
【答案】 （A）
【详解】
（1）根据《公路桥涵设计通用规范》4.3.1条4款，计算跨径l=40m的公路-Ⅰ级车道荷载，均布荷载：qk=10.5kN/m
集中荷载：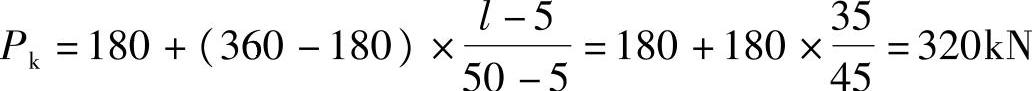
。
（2）根据《公路桥涵设计通用规范》表4.3.1-3，采用4车道，n=4。
（3）根据《公路桥涵设计通用规范》表4.3.1-4，横向折减系数ξ=0.67。
（4）跨中弯矩影响线竖标最大值为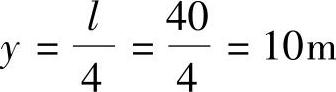
，影响线面积为ω=40×10/2=200m2。(www.daowen.com)
（5）冲击力增大系数1+μ=1.215。
（6）扭转影响对箱形截面梁内力的不均匀系数K=1.2。
（7）汽车荷载引起的跨中弯矩标准值为
Mk=K（1+μ）ξn（qkω+Pky）
=1.2×（1+0.215）×0.67×4×（10.5×200+320×10）
=20709kN·m
（A）正确。
【简解】
由汽车车道荷载产生的弯矩作用标准值
M=（1+μ）ξkn（Pkymax+qkω）
=1.215×0.67×1.2×4×（320×10+10.5×200）=20709kN·m
（A）正确。
真题 【11.3.2】～【11.3.3】 （2005年考题）
设计安全等级为二级的某公路桥梁，由多跨简支梁组成，其总体布置如图11.3.6所示。每孔跨径25m，计算跨径为24m，桥梁总宽10.5m，行车道宽度为8.0m，两侧各设1m宽人行步道，双向行驶二列汽车。每孔上部结构采用预应力混凝土箱形截面梁，桥墩上设立四个支座，支座的横桥向中心距为4.5m。桥墩支承在基岩上，由混凝土独柱墩身和带悬臂的盖梁组成。计算荷载：公路-Ⅰ级。
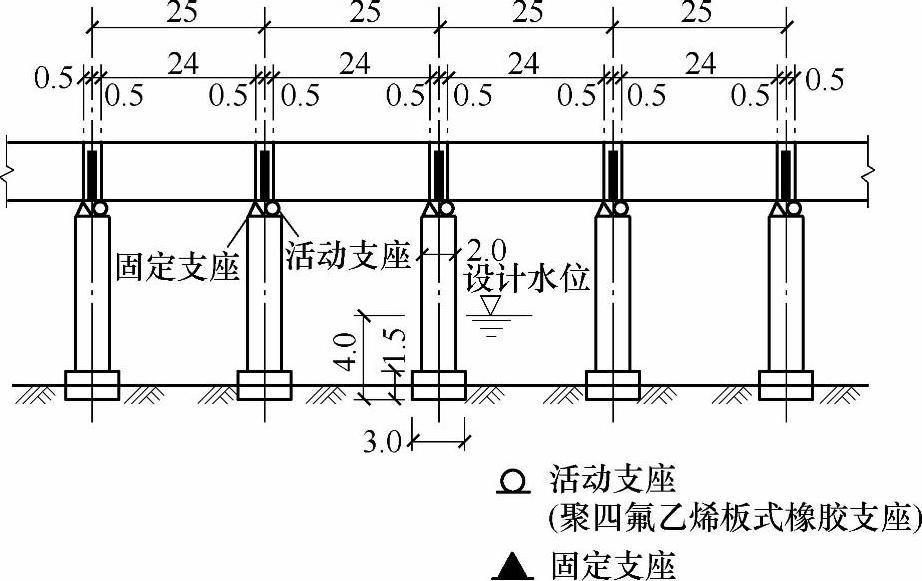
图 11.3.6
真题 【11.3.2】 （2005年考题）
假定冲击系数μ=0.2，试问，该桥主梁跨中截面在公路-Ⅰ级汽车车道荷载作用下的弯矩
标准值MQ1k（kN·m），应与下列何项数值最为接近？
（A）5500 （B）2750 （C）2300 （D）4580
【答案】 （A）
【详解】
（1）根据《公路桥涵设计通用规范》4.3.1条表4.3.1-3，8.0m行车道宽度按双车道计算，n=2。
（2）根据《公路桥涵设计通用规范》4.3.1条4款，计算跨径24m的公路-Ⅰ级车道荷载。
均布荷载：qk=10.5kN/m
集中荷载：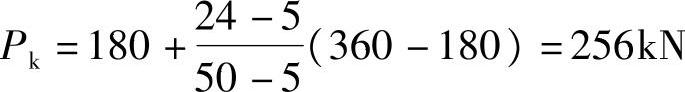
（3）冲击系数μ=0.2，冲击力增大系数1+μ=1.2
（4）车道荷载下的弯矩标准值为
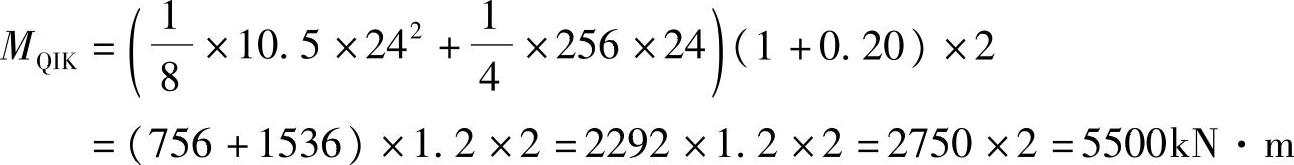
（A）正确。
【简解】
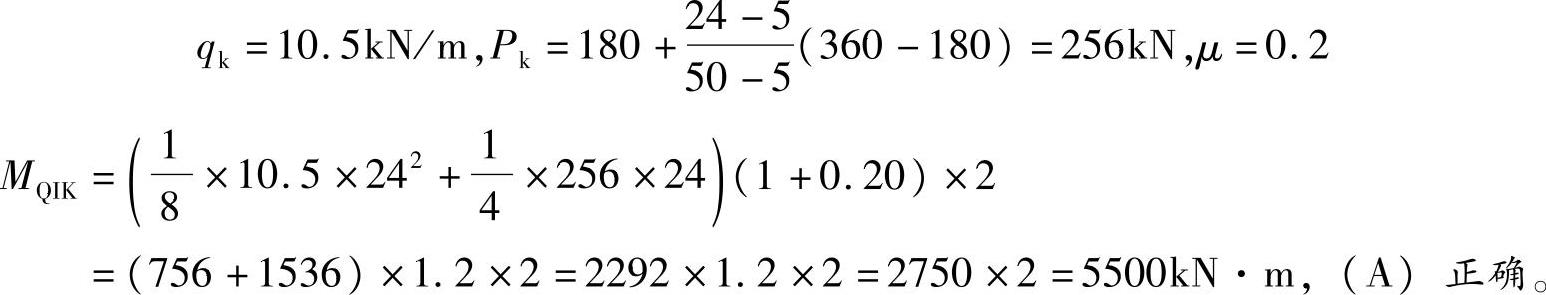
真题 【11.3.3】 （2005年考题）
假定冲击系数μ=0.2，试问，该桥主梁支点截面在公路-Ⅰ级汽车车道荷载作用下的剪力
标准值VQ1k（kN），应与下列何项数值最为接近？提示：按加载长度近似取24m计算。
（A）525 （B）1040 （C）900 （D）450
【答案】 （B）
【详解】
（1）根据《公路桥涵设计通用规范》4.3.1条表4.3.1-3，8.0m行车道宽度按双车道计算，n=2。
（2）根据《公路桥涵设计通用规范》4.3.1条4款，计算跨径24m的公路-Ⅰ级车道荷载，
均布荷载：qk=10.5kN/m
集中荷载：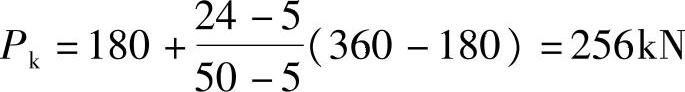
（3）冲击系数μ=0.2，冲击力增大系数1+μ=1.2。
（4）根据《公路桥涵设计通用规范》4.3.1条4款，计算剪力效应时车道荷载的集中荷载取1.2Pk。
（5）车道荷载下的剪力标准值
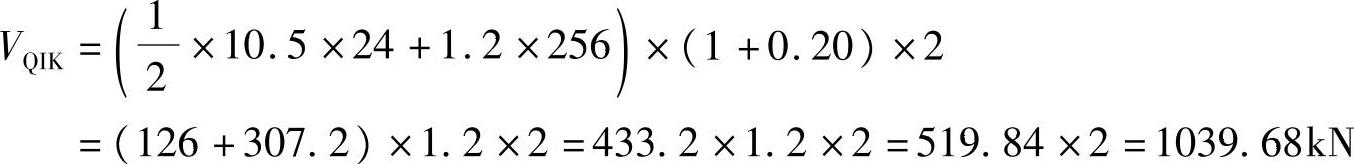
（B）正确。
【简解】
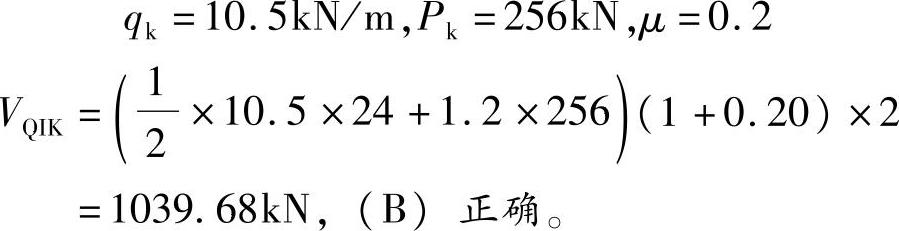
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
