整体式矩形实心简支板桥如图11.1.11所示，这种板桥是小跨径梁桥中最常用的桥型之一，因它具有以下的优点，故久用不衰。

（1）建筑高度小，适用于桥下净空受限制的桥梁。与其他类型的桥梁相比，可以降低桥头引道路堤高度和缩短引道长度。

（2）外形简单，制作方便，既便于采用土模技术，又便于进行工厂化成批生产。做成装配式板桥的预制构件时，重量不大，架设方便。

（3）无需专门配置抗剪钢筋，而只需按构造要求使部分主筋弯起，因而施工方法简单，模板和钢筋工程量都较省。

（4）对于高等级公路和城市立交工程，板桥（尤其是整体式板桥）又以极易满足斜、弯、坡以及S形、喇叭形等特殊要求而受到重视。

板桥的主要缺点是跨径不宜过大。板桥跨径超过一定限制时，截面便要显著增高，从而导致自重过大，截面材料使用上的不经济，使上述建筑高度小的优点也因之被抵消。

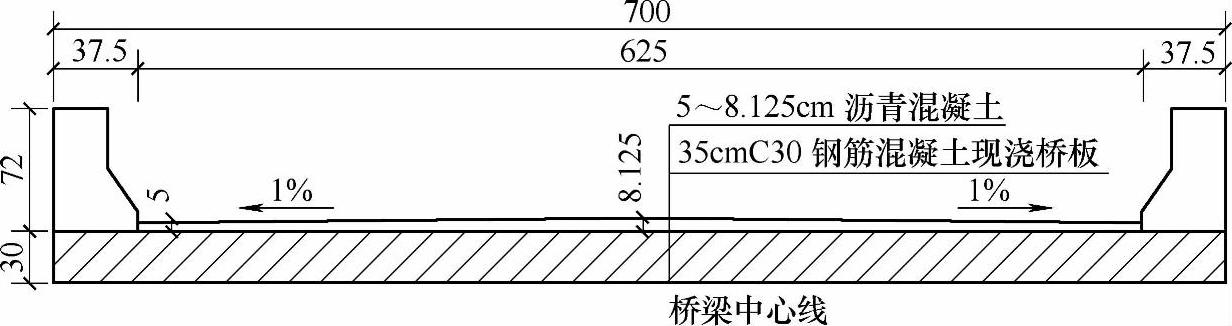
图11.1.11 整体式矩形实心简支板桥（尺寸单位：cm）

（一）板桥的受力特点

（1）在均布恒荷载作用下，桥跨板基本处于单向受力状态，其跨中截面单位宽度上的弯矩M_x可像简支梁跨中弯矩那样进行确定，而与之正交截面单位宽度上的弯矩M_y比弯矩M_x小得多。

（2）当车轮荷载作用在板中时，桥跨板处于双向受力状态。其跨中截面弯矩M_x沿板横向（y轴方向）是非均匀分布的，如图11.1.12所示，M_x随着距荷载作用点的距离增加而减小。而横向弯矩M_y虽大于均布荷载作用下的该值，但与M_x相比仍然很小。

（3）当车轮荷载作用在自由边附近时，M_x和M_y的分布规律与荷载作用在板中类似，但M_x数值较大，而M_y值较小。

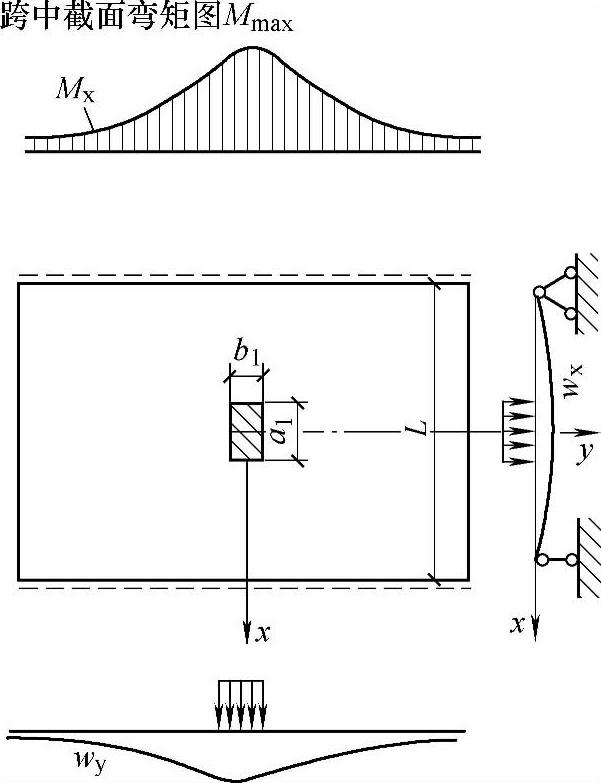
图11.1.12 板中弯矩的分布

根据上述受力特点，实际工程中整体式正交板桥通常采用更为实用的简化计算方法确定其内力，如荷载有效分布法。该法假定车轮荷载引起的跨中弯矩M_x由板的有效折算宽度来承担，认为车轮荷载沿板横向（y轴方向）是均匀分布在有效折算宽度内。由此计算出单位板宽度上的弯矩，最终确定单位板宽度上的受力钢筋数量。下一段即讨论此内容。

（二）板桥的构造

整体式正交简支板桥的板厚通常取跨径的1/20～1/15，但不宜小于10cm。

其配筋应与受力特点吻合。因此，除纵向受力主筋需通过计算确定外，还需布置一定数量的横向钢筋以承受车轮荷载引起的横向弯矩M_y（可通过计算确定）和防止混凝土收缩及温度变化引起的裂缝。

《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定：

9.2.3 行车道板内主钢筋直径不应小于10mm。在简支板跨中和连续板支点处，板内主钢筋间距不应大于200mm。

9.2.4 行车道板内主钢筋可在沿板高中心纵轴线的1/4～1/6计算跨径处按30°～45°弯起。通过支点的不弯起的主钢筋，每米板宽内不应少于三根，并不应少于主钢筋截面面积的1/4。

9.2.5 行车道板内应设置垂直于主钢筋的分布钢筋。分布钢筋设在主钢筋的内侧，其直径不应小于8mm，间距不应大于200mm，截面面积不宜小于板的截面面积的0.1%。在主钢筋的弯折处，应布置分布钢筋。

图11.1.13所示为整体式简支板桥构造的案例。该板桥的标准跨径6m、桥面净宽7.5m、两边有0.25m的安全带，计算跨径为5.69m，板厚32cm，约为跨径的1/18。纵向主筋直径为20mm，在中间2/3的板宽内间距为125cm，其余两侧的间距为11cm。主筋在跨径两端1/4～1/6的范围内呈30°弯起，分布钢筋按单位板宽上主筋面积的15%配置，直径为10mm，间距为20cm。

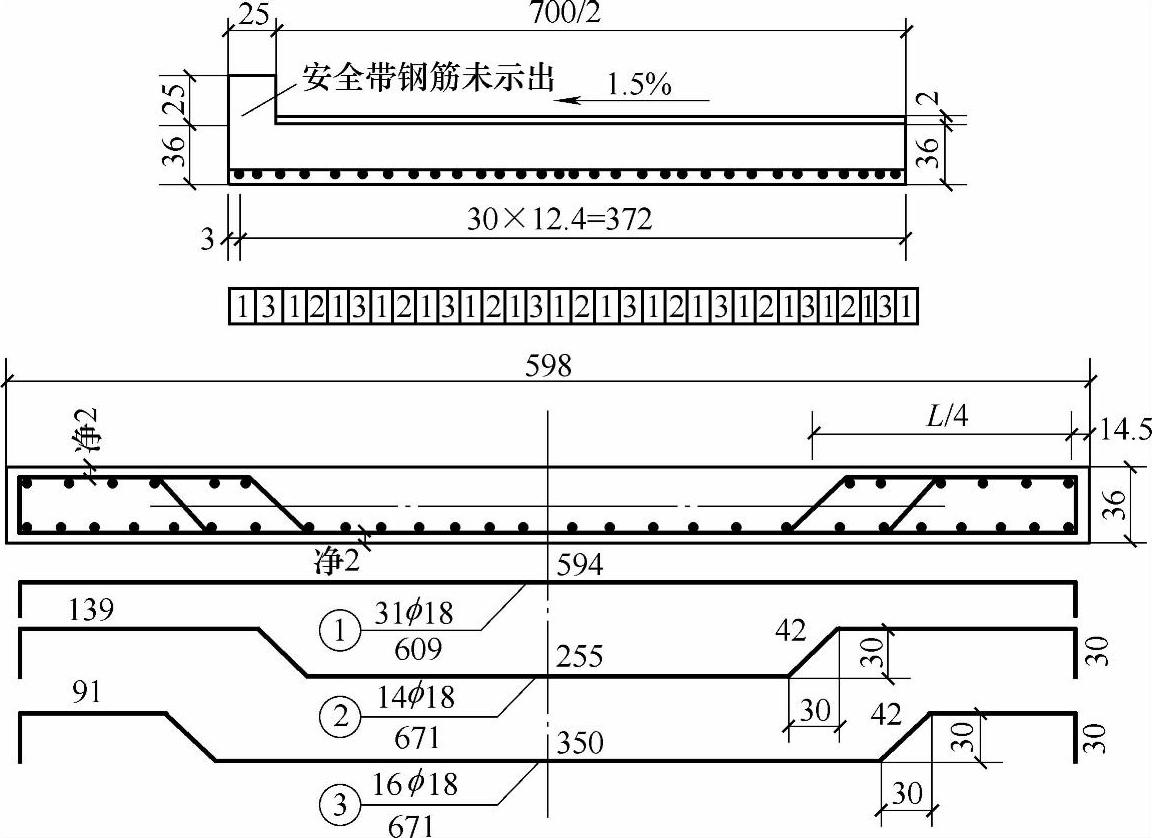
图11.1.13 正交板桥的构造（单位：cm）

在整体式钢筋混凝土板桥中，靠两侧边缘约1/6板宽范围内的主钢筋，通常要比中间板带部分密一些，一般增加15%（图11.1.14）。这是因为当车辆荷载靠近板边时，参与受力的板宽（荷载有效分布宽度）要比中间的小一些。对于承受重荷的宽桥，当荷载作用在板的两侧边缘时，板中部将产生负弯矩，因此还必须在板的顶部配置适量的横向钢筋。

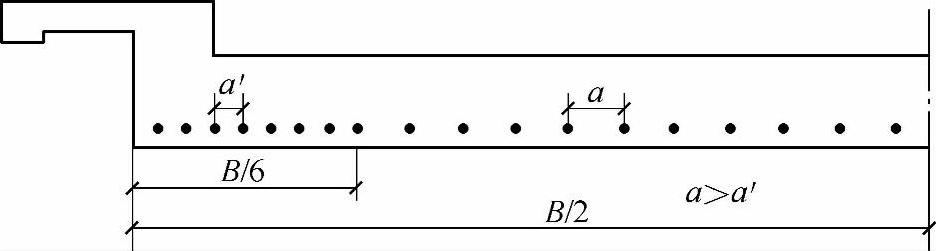
图11.1.14 钢筋混凝土整体式板桥的配筋

（三）板的荷载有效分布宽度

1.车轮荷载在板上的分布

作用在桥面上的车轮压力，通过桥面铺装层扩散分布在钢筋混凝土板面上，车轮与桥面的接触面实际上接近于椭圆，荷载要通过铺装层扩散分布，可见车轮压力在桥面板上的实际分布形状是很复杂的。

通常近似地把车轮与桥面的接触面看成是a₂×b₂的矩形面积，此处a₂是车轮垂直于板跨径方向的着地长度，b₂为车轮平行于板跨径方向着地的宽度，如图11.1.15所示。a₂和b₂值可从《公路桥涵设计通用规范》表4.3.1-2中查得。荷载在铺装层内的扩散程度，对于混凝土或沥青面层可偏安全地假定呈45°角扩散。

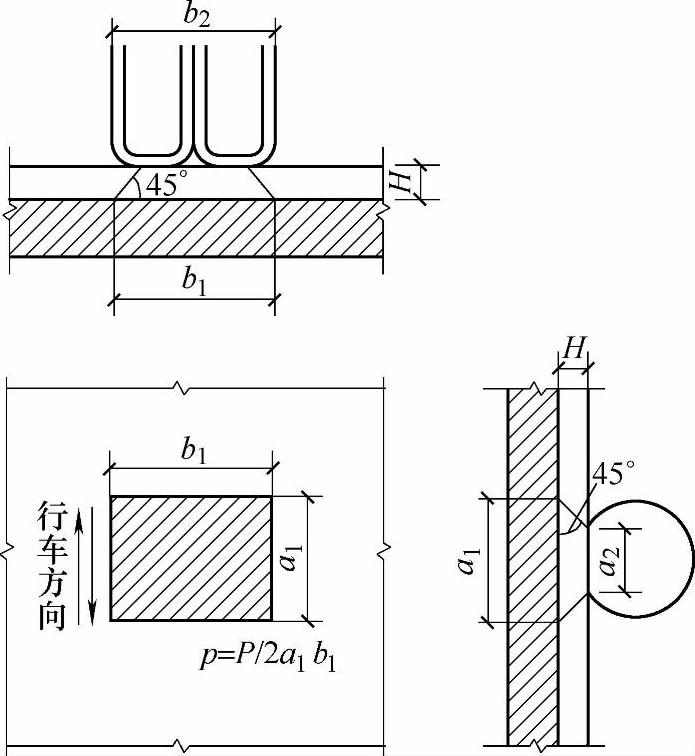
图11.1.15 车辆荷载在板面上的分布

因此，作用于钢筋混凝土承重板上荷载分布的矩形压力面的宽度为

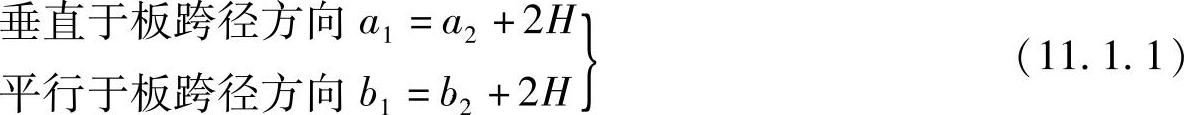
式中 H——铺装层的厚度。

应取车辆荷载的后轮作为计算荷载作用于桥面板上，其局部分布的荷载强度为

式中 P——车辆荷载的轴重。

2.板的有效工作宽度

桥面板在局部分布荷载的作用下，不仅直接承压部分（承压面为a₁×b₁）的板带参与工作，而且与其相邻的部分板带也分担一部分荷载。因此，在桥面板荷载的计算中，需确定板的有效工作宽度（也称荷载有效分布宽度）。

单向板的受力状态如图11.1.16所示，跨径为l的单向板，其上作用以a₁×b₁为分布面积的荷载，板在计算跨径x方向和垂直于计算跨径的y方向分别产生挠曲变形w_x和w_y，板条沿y方向单位宽度所分担弯矩m_x（kN·m/m）呈菱形分布，在荷载中心处，板条负担的弯矩最大（其值为m_x，max），离荷载越远的板条所承受的弯矩越小。

如果以a×m_x，max的矩形面积等代曲线图形面积，即

a×mx，max=∫mxdy=M

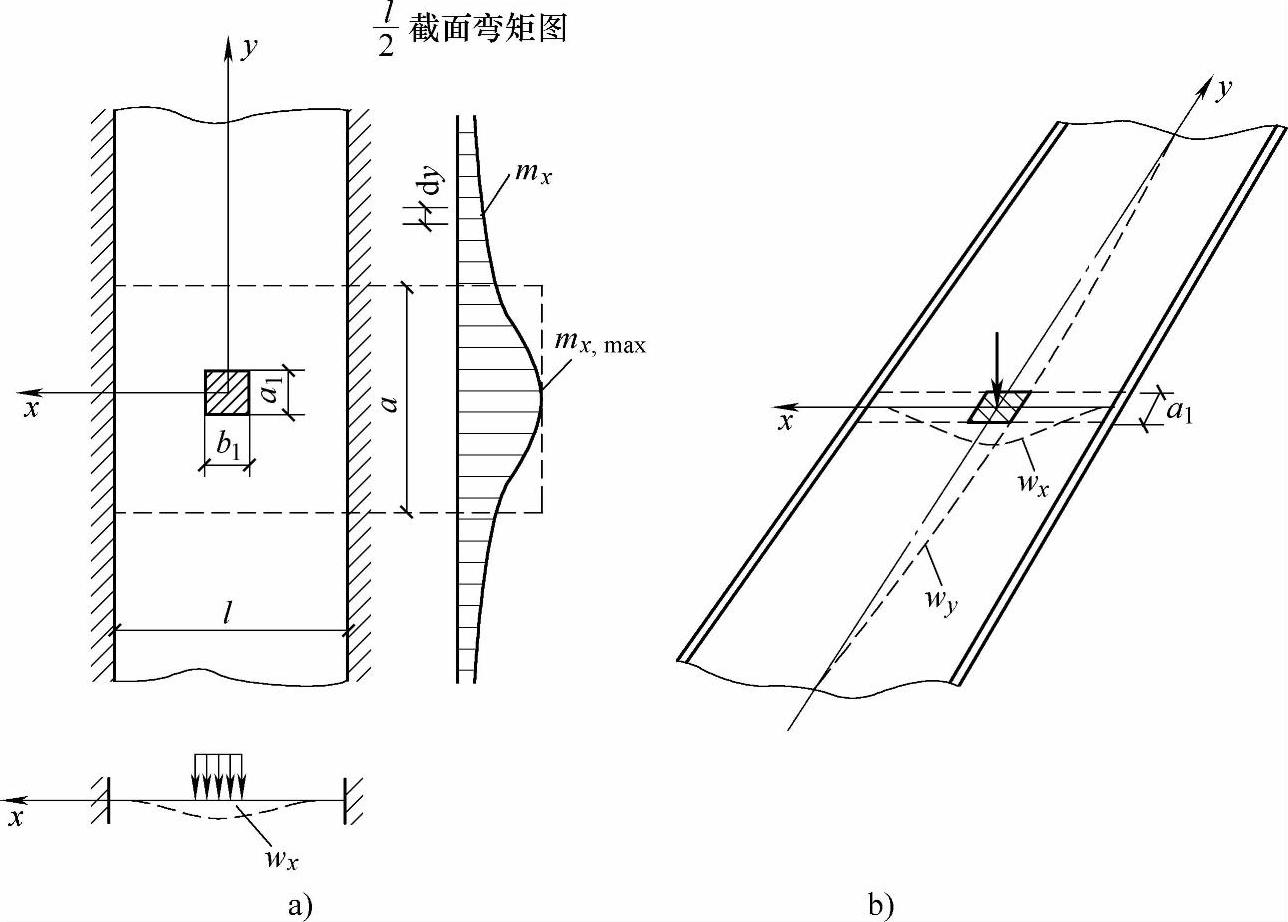
图11.1.16 单向板的跨中截面弯矩分布

则得弯矩图的换算宽度（荷载的有效工作宽度）为

式中 a——板的有效分布宽度；

M——车轮荷载产生的跨中总弯矩；

m_x，max——荷载中心处的最大单宽弯矩值（单位：kN·m/m）。

《公路钢筋混凝土及预应力混凝土桥涵设计规范》对板的荷载有效分布宽度规定如下。4.1.3 计算整体单向板时，通过车轮传递到板上的荷载分布宽度应按下列规定计算：

1 平行于板的跨径方向的荷载分布宽度

b=b₁+2h （4.1.3-1）

2 垂直于板的跨径方向的荷载分布宽度

1）单个车轮在板的跨径中部时(www.daowen.com)

2）多个相同车轮在板的跨径中部时，当各单个车轮按公式（4.1.3-2）计算的荷载分布宽度有重叠时

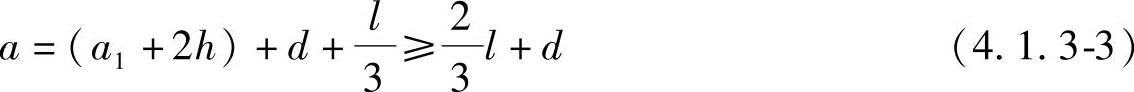
3）车轮在板的支承处时

a=（a₁+2h）+t （4.1.3-4）

4）车轮在板的支承附近，距支点的距离为x时

a=（a₁+2h）+t+2x （4.1.3-5）

但不大于车轮在板的跨径中部的分布宽度；

5）按本条算得的所有分布宽度，均不得大于板的全宽度；

6）彼此不相连的预制板，车轮在板内分布宽度不得大于预制板宽度。

式中 l——板的计算跨径；

h——铺装层厚度；

t——板的厚度；

d——多个车轮时外轮之间的中距；

a₁、b₁——垂直于板跨和平行于板跨方向的车轮着地尺寸。

现将上述荷载分布宽度表示于图11.1.17。

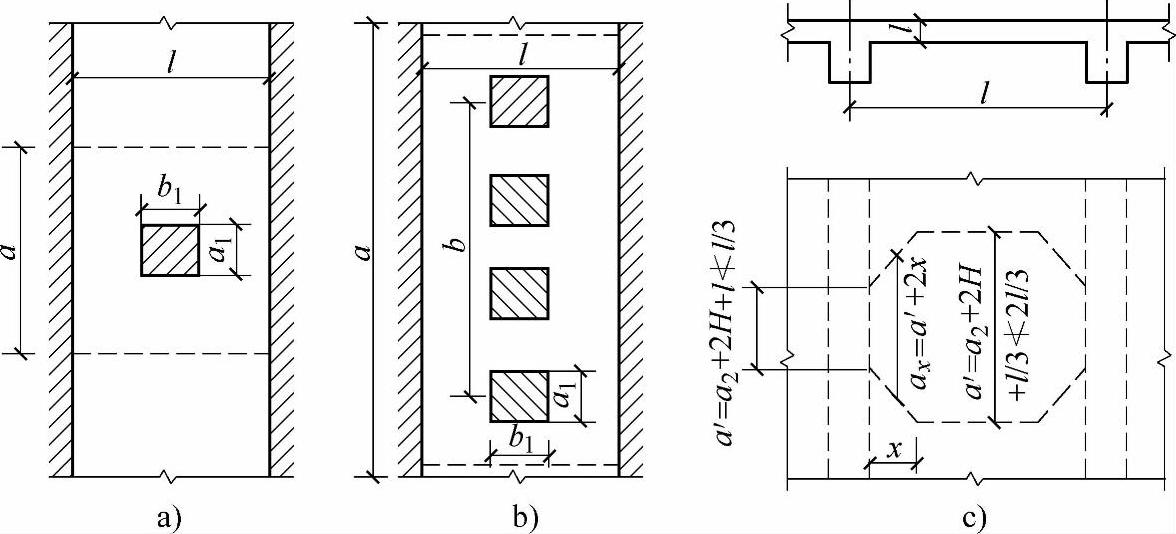
图11.1.17 板的荷载有效分布宽度

a）单个车轮在板的跨径中部 b）多个相同车轮在板的跨径中部 c）车轮在板的支承处

（四）斜板桥

1.斜板桥的受力特点

斜（交）板桥是指桥轴线与支承线不相互垂直的桥梁（图11.1.18）。斜交角φ是指桥轴线与支承线的垂线的夹角，宽度b是垂直于桥纵轴线的板宽，板的斜跨径是lφ。

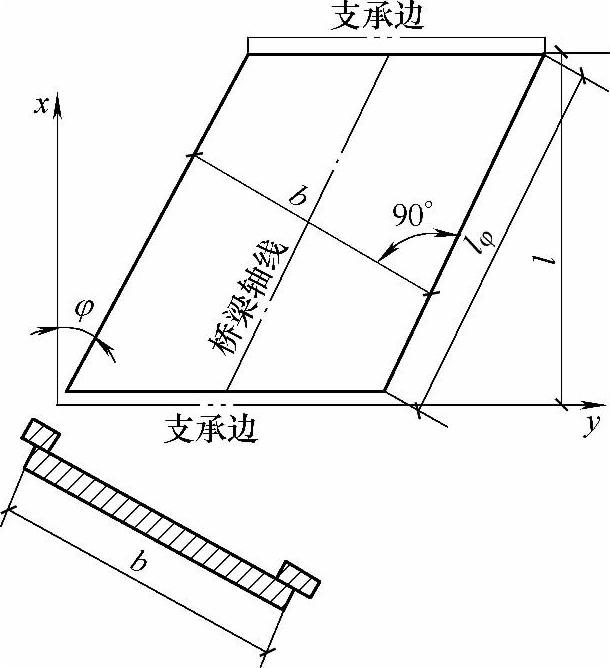
图11.1.18 斜板的尺寸图

（1）斜板的荷载有向两支承边之间最短距离方向传递的趋势（图11.1.19）。在宽跨比（b/lφ）较大的斜板中部，其最大主弯矩方向（即在垂直于该方向的截面上没有扭矩）几乎接近与支承边垂直。边缘的主弯矩方向虽接近平行于自由边，但仍有向支承边垂线方向偏转的趋势。

图11.1.19 斜板的主弯矩方向

（2）斜板各角点的受力情况可以用图11.1.20中，以ABCD为支点的Z字形连续梁（三跨连续梁）来比拟。

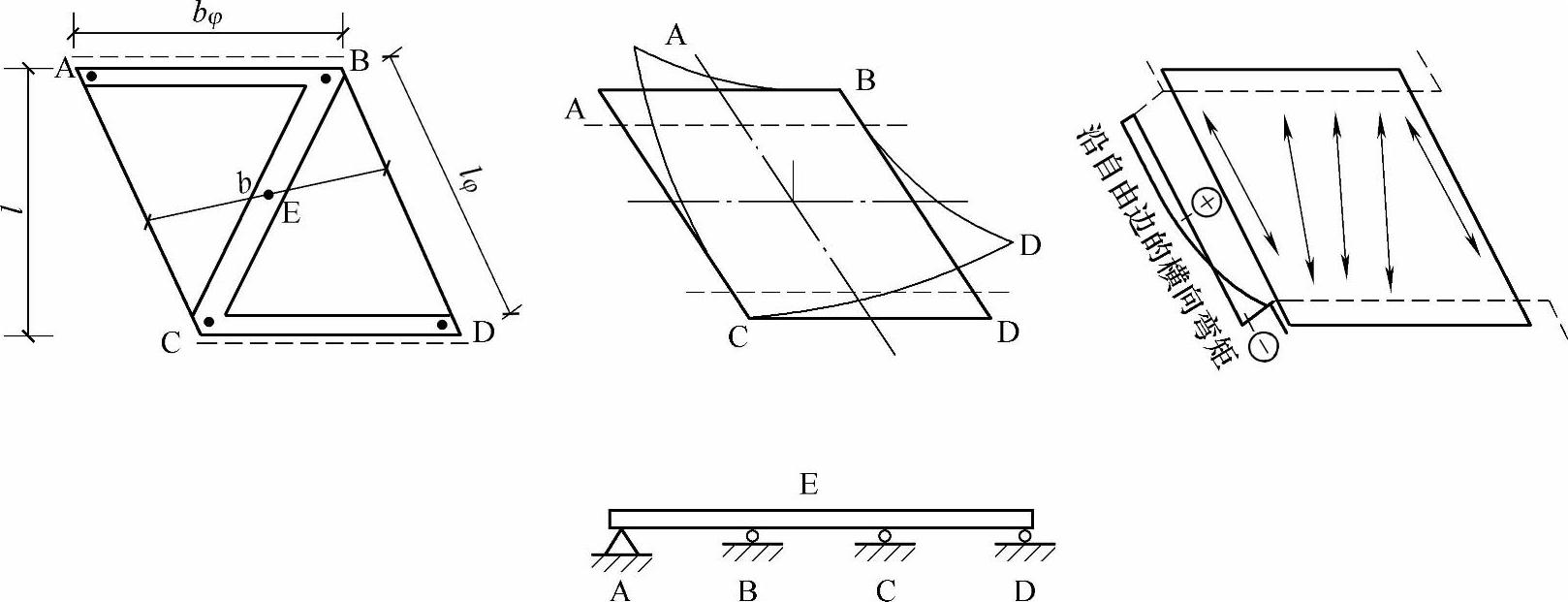
图11.1.20 比拟锐角连续梁

在钝角B、C处产生接近于跨中弯矩值的相当大的负弯矩，其方向垂直于钝角的二等分线，其值随φ的增大而增加，但分布范围较小，并迅速削减。

斜板在支承边上的反力很不均匀。以钝角B、C处的反力最大，锐角A、D处的反力最小，当斜交角与宽跨比都较大时，甚至可能出现负反力，使锐角向上翘起。此时若固定角点，势必导致板内有较大的扭矩。

（3）当斜交角在15°以内时，斜交的影响可以忽略，因此《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定：当φ≤15°时，近似地取板的斜长lφ为计算跨径按正交板桥计算。

《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定：

4.1.4 当整体式斜板桥的斜交角（板的支承轴线的垂直线与桥纵轴线的夹角）不大于15°时，可按正交板计算，计算跨径为：当l/b≤1.3时，按两支承轴线间垂直距离的正跨径计算；当l/b＞1.3时，按顺桥向纵轴线的斜跨径计算；以上l为斜跨径，b为垂直于桥纵轴线的板宽。

装配式铰接斜板桥的预制板块，可按宽为两板边垂直距离，计算跨径为斜跨径的正交板计算。

2.斜板桥钢筋布置

《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定：

9.2.7 斜板的钢筋可按下列规定布置（图9.2.7）：

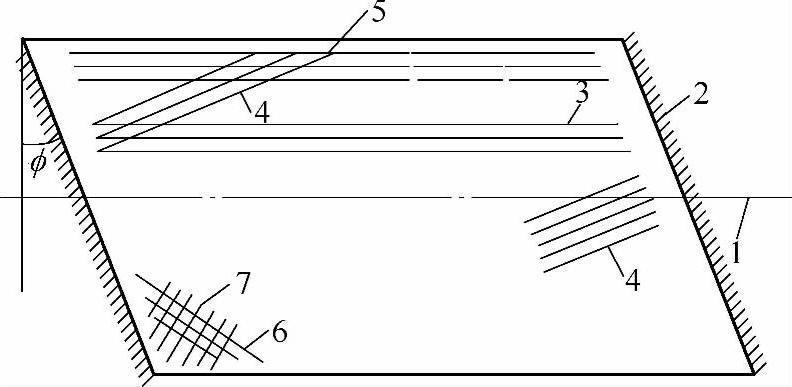
图9.2.7 斜板桥钢筋布置

1—桥纵轴线 2—支承轴线 3—顺桥纵轴线钢筋 4—与支承轴线正交钢筋 5—自由边钢筋带 6—垂直于钝角平分线的钝角钢筋 7—平行于钝角平分线的钝角钢筋

1 当整体式斜板的斜交角（板的支座轴线的垂直线与桥纵轴线的夹角）不大于15°时，主钢筋可平行于桥纵轴线方向布置。当整体式斜板斜交角大于15°时，主钢筋宜垂直于板的支座轴线方向布置，此时，在板的自由边上下应各设一条不少于三根主钢筋的平行于自由边的钢筋带，并用箍筋箍牢。在钝角部位靠近板顶的上层，应布置垂直于钝角平分线的加强钢筋，在钝角部位靠近板底的下层，应布置平行于钝角平分线的加强钢筋，加强钢筋直径不宜小于12mm，间距100～150mm，布置于以钝角两侧1.0～1.5m边长的扇形面积内。

2 斜板的分布钢筋宜垂直于主钢筋方向设置，其直径、间距和数量可按本规范第9.2.5条办理。在斜板的支座附近宜增设平行于支座轴线的分布钢筋；或将分布钢筋向支座方向呈扇形分布，过渡到平行于支承轴线。

图11.1.21列出了上述整体式斜板（lφ≤1.3b）钢筋构造规定的示意图。

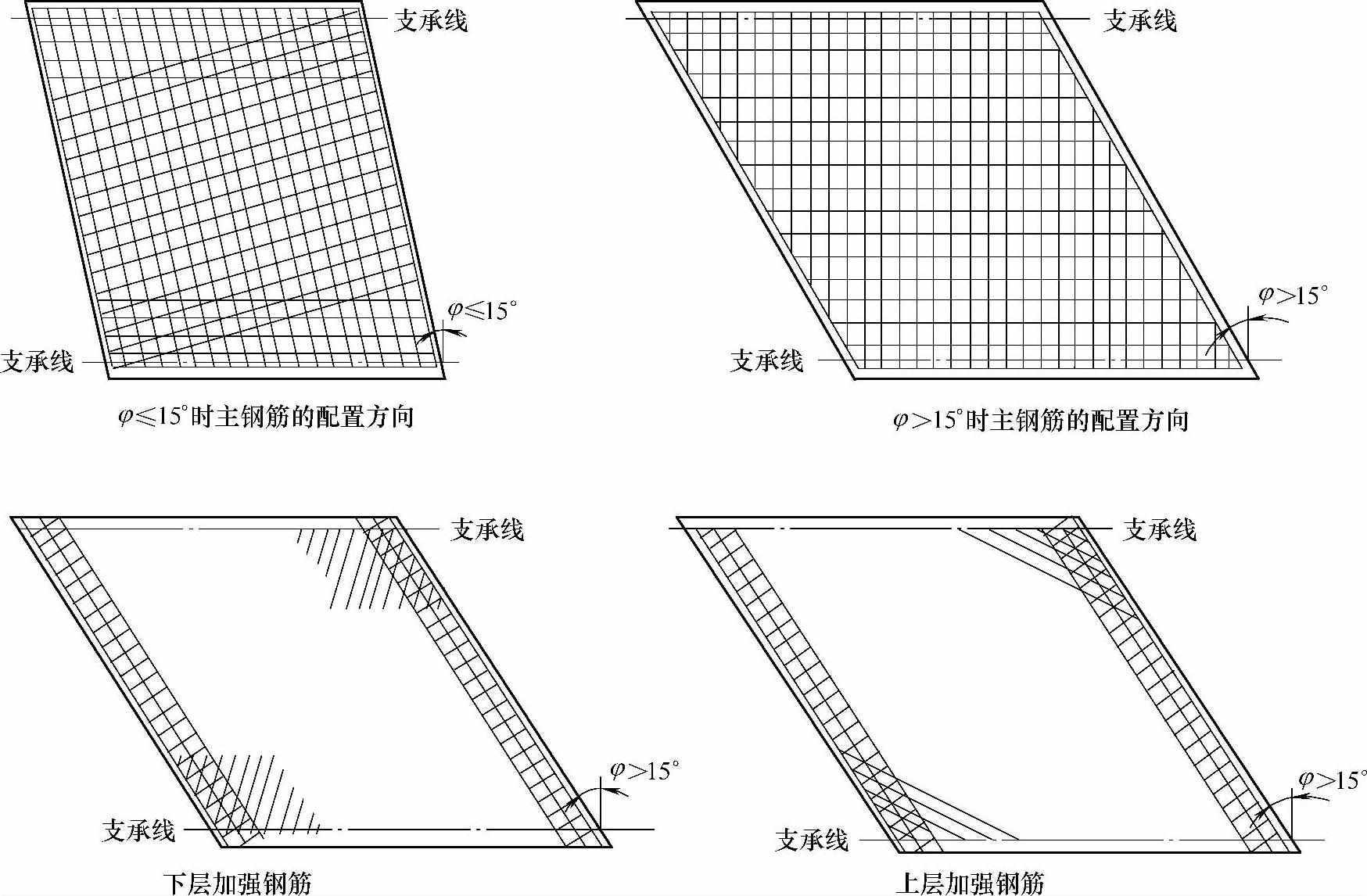
图11.1.21 整体式斜板（lφ≤1.3b）的钢筋构造

真题 【11.1.1】 （2003年考题）

某公路桥梁由整体式钢筋混凝土板梁组成，计算跨径为12.0m，斜交角30°，总宽度为9m，梁高为0.7m。在支承处每端各设三个支座。其中一端用活动橡胶支座（A₁、A₂、A₃）；另一端用固定橡胶支座（B₁、B₂、B₃）。其平面布置如图11.1.22所示。试问，在恒荷载（均布荷载）条件下各支座垂直反力大小的正确判断，应为下列何项所述？

（A）A₂与B₂的反力最大 （B）A₂与B₂的反力最小

（C）A₁与B₃的反力最大 （D）A₃与B₁的反力最大

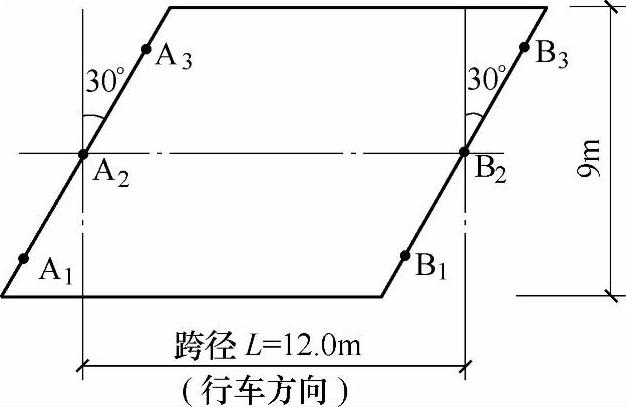
图 11.1.22

【答案】 （D）

【解答】 斜板桥的受力特点，斜交板在均布荷载下，钝角处反力最大，锐角处反力最小。即A₃与B₁的反力最大，（D）正确。