在移动荷载作用下，可以求出简支梁上任一指定截面处的最大弯矩。但在梁的所有各截面最大弯矩中，又有最大的，称为简支梁的绝对最大弯矩。

要确定简支梁的绝对最大弯矩，须解决两个问题：①绝对最大弯矩发生在哪一个截面？②此截面发生最大弯矩值时的荷载位置。

当梁上作用的移动荷载都是集中荷载时，梁在集中荷载组作用下，无论荷载在任何位置，弯矩图的顶点总是在集中荷载作用点处。因此可以断定，绝对最大弯矩必定是发生在某一集中荷载作用点处的截面上。

究竟发生在哪一荷载位置时的哪一个荷载下面。可先任选一集中荷载，看荷载在什么位置时，该荷载作用点处截面的弯矩达到最大值。然后按同样方法，分别求出其他各荷载作用点处截面的最大弯矩，再加以比较，即可确定绝对最大弯矩。

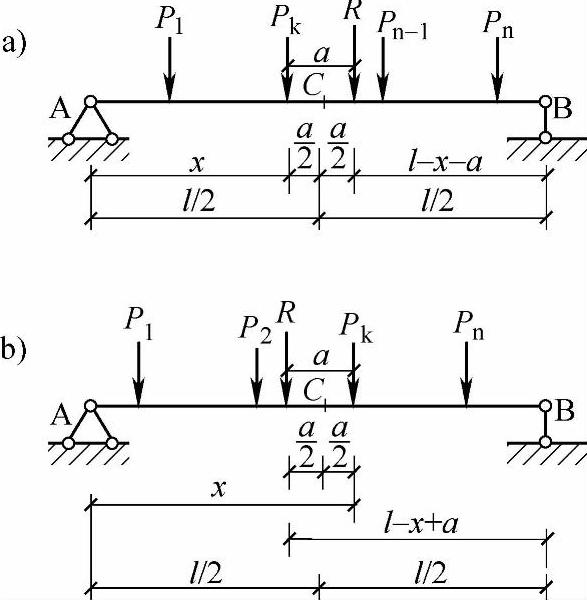
图 9.6.1

如图9.6.1a所示为一简支梁AB承受一组数值和间距不变的集中移动荷载作用，在荷载组中指定某一荷载P_k，它与支座A的距离为x，以R表示作用在梁上的所有荷载的合力，以a表示R与P_k之间的距离，R_A代表左支座A的反力。现设P_k在合力R的左边（如图9.6.1a所示）。由∑M_B=0，可得

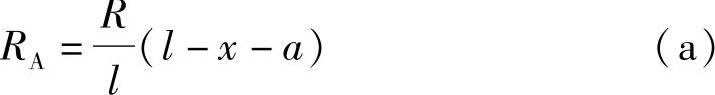
P_k作用点所在截面的弯矩M_x为

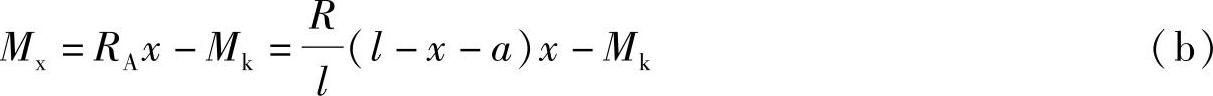
式中M_k表示P_k以左各荷载对P_k作用点的力矩之和，是与x无关的常数。为求M_x的极值，可令

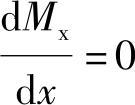
则

即

如果P_k在合力R的右边（图9.6.1b），同理可得

综合式（9.6.1a）和式（9.6.1b），可以得到P_k作用点所在截面弯矩为最大值的条件为

上式表明，当梁上所有荷载的合力R与P_k恰好位于梁的跨度中点两侧的对称位置时，P_k作用截面的弯矩达到最大值。

将式（9.6.2）代入式（b）即得弯矩最大值为

利用以上所述，我们可将各个荷载作用点截面的最大弯矩找出，将它们加以比较而得出绝对最大弯矩。不过，当荷载数目较多时，这仍是较麻烦的。实际计算时，宜事先估计发生绝对最大弯矩的临界荷载。因为简支梁的绝对最大弯矩总是发生在梁的中点附近，故可设想，使梁中点截面产生最大弯矩的临界荷载，也就是发生绝对最大弯矩的临界荷载。经验表明，这种设想在通常情况下都是正确的。据此，计算绝对最大弯矩可按下述步骤进行：首先确定使梁中点截面发生最大弯矩的临界荷载P_k，然后移动荷载组使P_k与梁上荷载的合力R对称于梁的中点，再计算此时P_k作用点截面的弯矩，即得绝对最大弯矩。

【9.6.1】 确定简支梁在吊车荷载作用下的绝对最大弯矩

要求：求图9.6.2a所示吊车梁的绝对最大弯矩，并与跨中截面C的最大弯矩进行比较。已知P₁=P₂=P₃=P₄=82kN。

【解答】 （1）求跨中截面C的最大弯矩M_Cmax。

1）作M_C影响线如图9.6.2b所示。

2）判别临界荷载。由于当P₂（或P₃）位于影响线顶点（图9.6.2）时，有较多的荷载位于顶点附近和梁上，故可设P₂（或P₃）为P_k，用式（9.5.1）判别知P₂（或P₃）为临界荷载。

3）计算M_Cmax。P₁、P2、P3、P4作用点处所对应的M_C影响线上的竖标如图9.6.2b。

M_Cmax=P₁y₁+P₂y₂+P₃y₃+P₄y₄=82×（1.25+3.0+2.25+0.5）kN·m=574kN·m

（2）求AB梁的绝对最大弯矩M_max。由图9.6.2a可见，绝对最大弯矩将发生在荷载P₂（或P₃）下面的截面。先求荷载P₂为P_k的最大弯矩：

1）梁上荷载的合力R

R=82×4kN=328kN

2）确定R与P_k的间距a

由于P₁=P₂=P₃=P₄，故其合力R与P₂和P₃的距离应相等，可求得

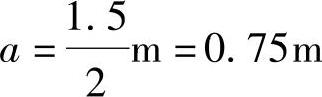
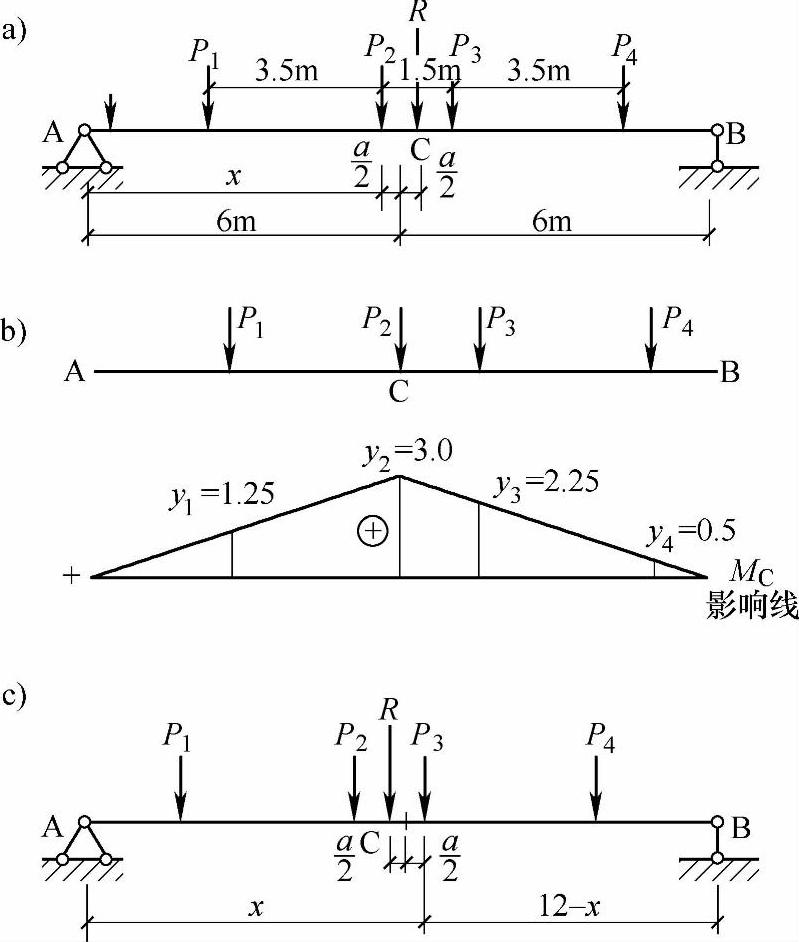
图 9.6.2

3）确定P_k作用点位置

由图9.6.2a可知P_k与合力R应位于梁中点两侧的对称位置上，因而P_k=P₂距跨中为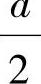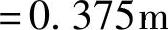（图9.6.2a）

4）计算最大弯矩

由式（9.6.3）求得

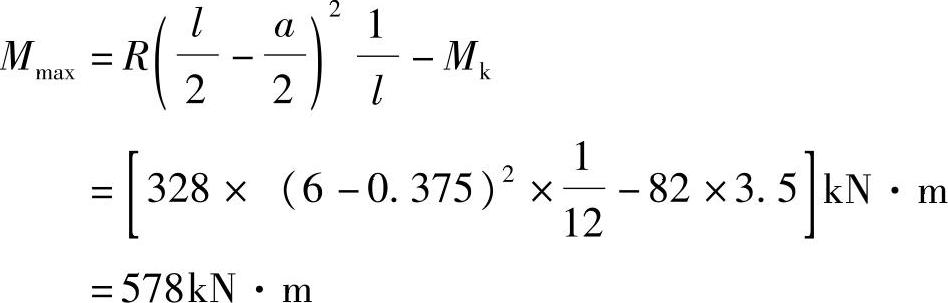
再求P₃为P_k时的最大弯矩：

由于对称，P₃为P_k时其荷载位置应如图9.6.2c所示。故其作用截面处的最大弯矩应与P₂为P_k时的最大弯矩相等。

由以上计算可见，绝对最大弯矩为

M_max=578kN·m

绝对最大弯矩比跨中截面最大弯矩大（578-574）/574=0.7%

真题 【9.6.2】 （1999年一级考题）

12m跨简支钢吊车梁，设有两台起重量Q=50/10t桥式吊车，每台吊车大车轮压分布及桥架宽度资料如图9.6.3所示。在一跨吊车梁上只可能有三个轮子同时作用，梁自重忽略不计。

图 9.6.3

试问，梁上最大弯矩作用截面距最近梁端支座的距离应为以下何项数值？(www.daowen.com)

（A）3.58m （B）5.44m （C）5.85m （D）6.00m

【答案】 （B）

【分析】 题目为影响线的简支梁的绝对最大弯矩问题。一般应求出合力及其位置，然后试验梁上集中荷载与合力对称位于梁中点两侧时，计算梁作用点截面的弯矩，即为绝对最大弯矩的位置，即可确定此位置距离支座的位置。

题目为两台吊车4个轮压，考虑轮压的距离位置，最不利的情况只有3个荷载在梁上，而且中间一个荷载应该与合力R对称位于梁中点两侧。

如图9.6.4所示，考虑一跨简支梁的作用。用合力矩定理，求合力及位置。

则梁上最大弯矩作用位置即绝对最大弯矩的截面位置，即与合力R对称位于中点两侧的集中荷载作用点，此点距离较近支座的距离为b。

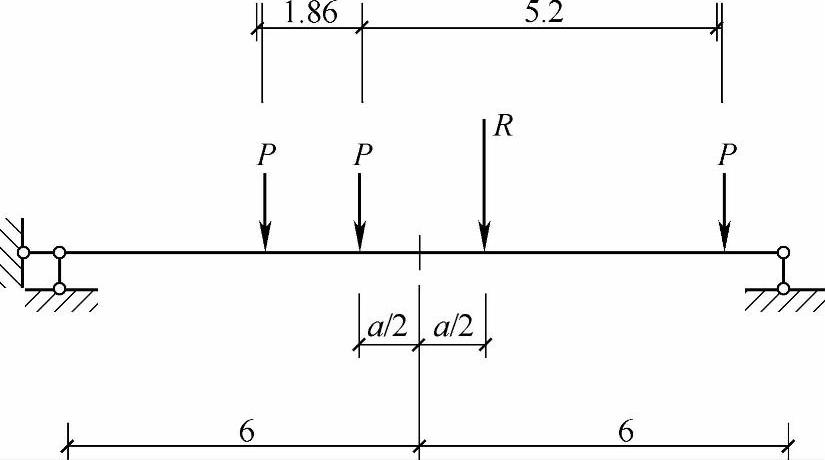
图 9.6.4

有了绝对最大弯矩的概念，根据题目要求，只要确定绝对最大弯矩的位置即可，并不需要求出绝对最大弯矩。

【解答】

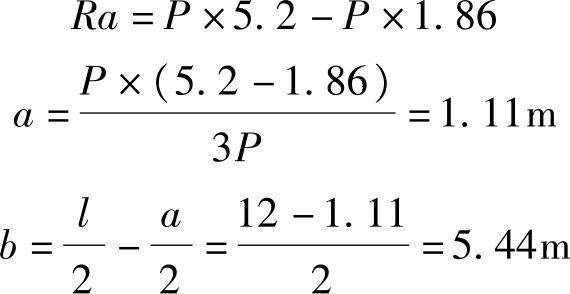
真题 【9.6.3】 （2007年一级考题）

某多跨厂房，中列柱的柱距12m，采用钢吊车梁。在吊车梁上行驶两台重级工作制的软钩桥式吊车，起重量Q=50/10t，小车重g=16.6t，吊车桥架跨度L_k=31.5m，最大轮压标准值P=453.7kN，每台吊车的轮压分布如图9.6.5所示。

试问，由两台吊车垂直荷载产生的吊车梁的最大弯矩设计值（kN·m），应与下列何项数值最为接近？

（A）2677 （B）2944

（C）3747 （D）4030

图 9.6.5

【答案】 （D）

【分析】 题目为影响线的简支梁的绝对最大弯矩问题。一般应求出合力及其位置，然后试验梁上集中荷载与合力对称位于梁中点两侧时，计算集中荷载作用点截面的弯矩，几个可能的试荷载所得结果比较最大的即为所求。

题目为两台吊车4个轮压，定性判断，考虑轮压的距离位置，最不利的情况只有3个荷载在梁上，而且中间一个荷载在中点附近最不利。

【解答】

（1）求合力及位置，用合力矩定理，如图9.6.6所示

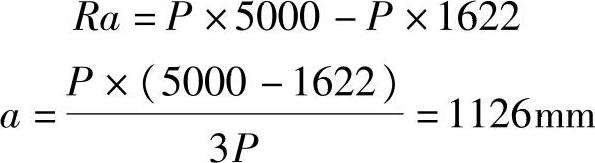
（2）代入公式（其中a为试算荷载与合力距离，M_k为梁上与合力异侧的荷载对试算荷载作用点的力矩总和，这时a前面总取负号）

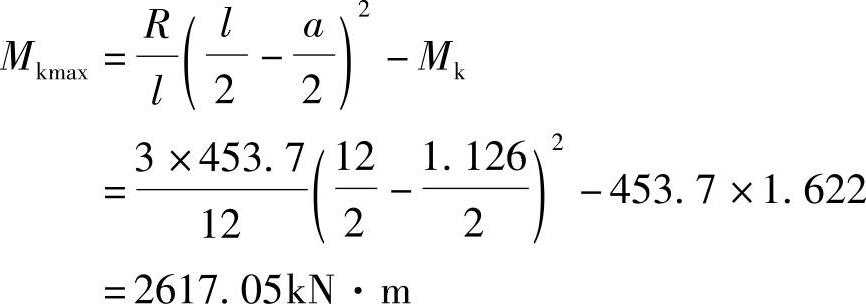
（3）根据《建筑结构荷载规范》3.2.4条，设计值：活荷载乘1.4

根据《建筑结构荷载规范》6.3.1条，动力系数1.1。

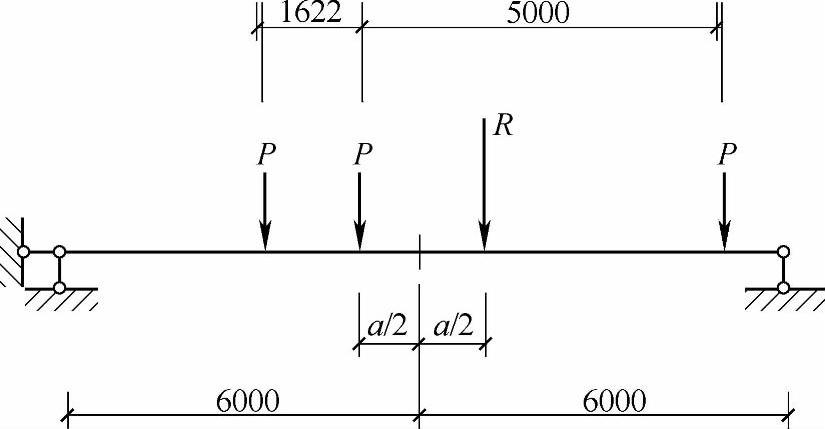
图 9.6.6

跨中弯矩最大值设计值

M=1.4×1.1×M_Kmax=1.4×1.1×2617.05=4030.26kN·m

真题 【9.6.4】 （2008年二级考题）

某跨度为6m的钢筋混凝土简支吊车梁，安全等级为二级，环境类别为一类，计算跨度l₀=5.8m，承受两台A5级起重量均为10t的电动软钩桥式吊车，吊车的主要技术参数见表9.6.1。

表9.6.1 吊车主要技术参数表（g=10m/s²）

当进行承载力计算时，在吊车竖向荷载作用下，吊车梁的跨中最大弯矩设计值M（kN·m），应与下列何项数值最为接近？

提示：该两台吊车在6m跨吊车梁上产生的最大弯矩位置如图9.6.7所示。

（A）279 （B）293

（C）310 （D）326

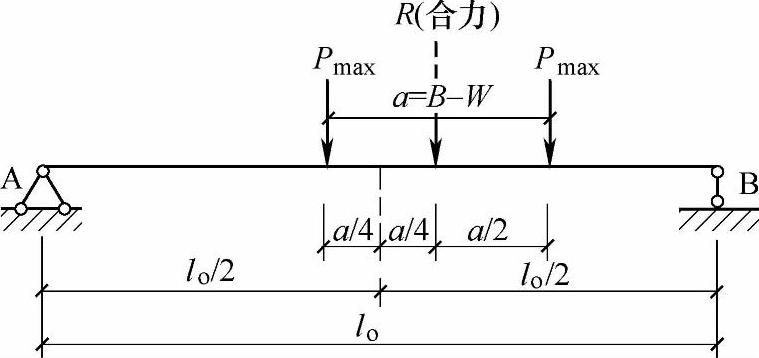
图 9.6.7

【答案】 （D）

【解答】 题目为影响线的简支梁的绝对最大弯矩问题。一般应求出合力及其位置，然后试算梁上集中荷载与合力对称位于梁中点两侧时，计算梁作用点截面的弯矩，几个可能的试荷载所得结果相比较，最大的即为所求。

题目只有两个荷载而且大小相等，合力即为二力中间位置，对称情况，只需试算一个集中力与合力对称位于梁中点两侧，如图9.6.7所示，位于中点左侧二力间距的1/4处，可以利用公式，也可以直接用静力平衡求解。

（1）公式（其中a^*为试算荷载与合力距离，M_k为梁上与合力异侧的荷载对试算荷载作用点的力矩总和，这时a^*前面总取负号）。

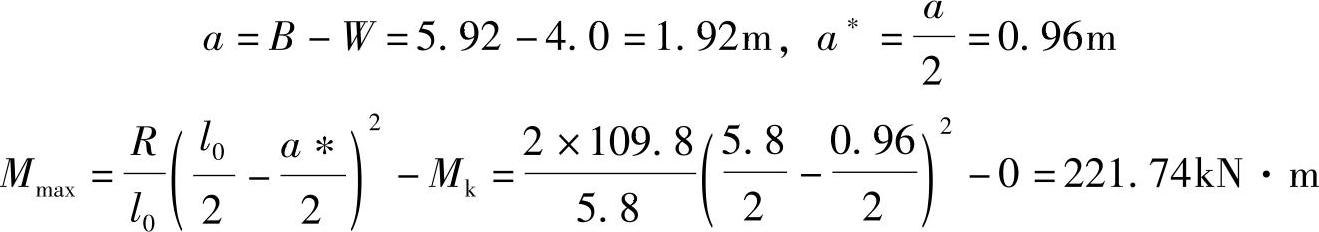
（2）直接静力计算。先求支座反力，再求中点左侧荷载作用点的弯矩（这点很重要，必须由绝对最大弯矩的概念知道求什么位置的弯矩）

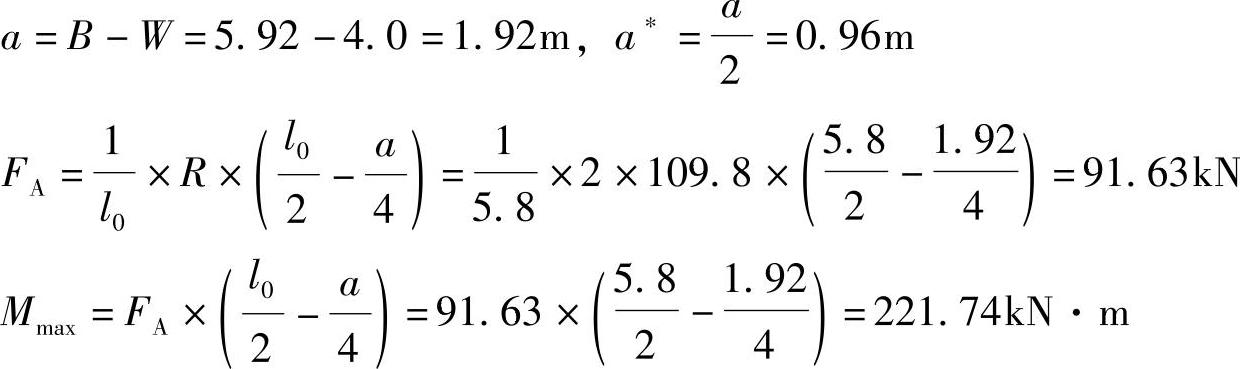
根据《建筑结构荷载规范》3.2.4条，设计值：恒荷载乘1.2，活荷载乘1.4

根据《建筑结构荷载规范》5.3.1条，A5级动力系数1.05

跨中弯矩最大值设计值

M=1.4×1.05×M_Kmax=1.4×1.05×221.74=325.96kN·m