(一)一个移动集中荷载
我们知道,在单个集中荷载作用下产生的某量值的数值,等于此力与其作用点之下相应影响线竖距的乘积。因此,最不利荷载位置是这个集中荷载作用在影响线的竖距最大处。
(二)行列荷载
所谓行列荷载,一般是指一系列彼此间距不变的移动的竖向集中荷载或竖向均布荷载,如铁路标准列车荷载及公路桥涵的汽车标准荷载等。
由于这类荷载的荷载数目较多,确定最不利荷载位置的方法分两步来解决。
第一步,求出使所研究的量值S产生极值的荷载位置。这个荷载位置称为临界荷载位置。
第二步,从有限个临界荷载位置中选出最不利荷载位置,也就是从S的极大值中选出最大值,从极小值中选出最小值。
根据临界荷载位置的定义可知,当荷载移动到该位置使所求量值S为极大值时,行列荷载由该位置不论向左或向右移动一微小距离,S值一定减小,即其增量ΔS≤0。如何找到这个位置呢?可以证明(此处从略)当系列集中荷载必须有一个集中荷载Pk位于所求量值影响线图形的顶点处才有可能使之产生极值(注意这只是必要条件而非充分条件)。我们将能使所研究量值S产生极值的荷载位置称为临界荷载位置,置于影响线顶点的该荷载Pk称为临界荷载。下面对影响线图形为三角形的情况推导出荷载临界位置判别准则。
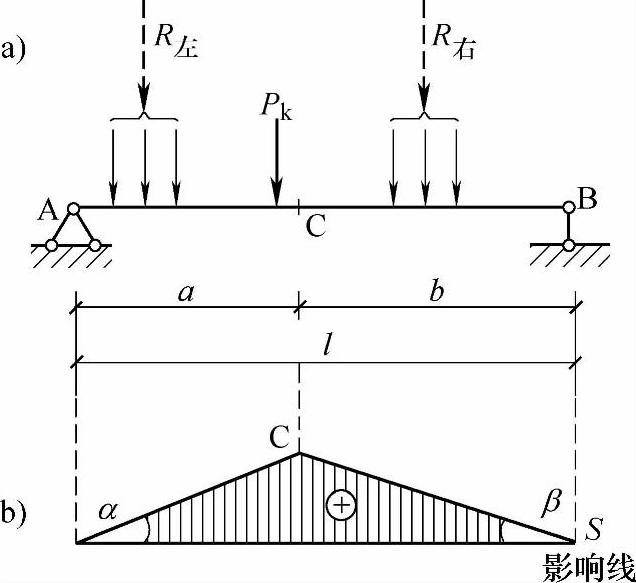
图 9.5.4
图9.5.4a、b分别表示一大小、间距不变的移动荷载组和某一量值S的三角形影响线。现在来确定S有最大值时荷载的最不利位置。
在移动荷载中选定一个Pk,将Pk置于S影响线的顶点上,以R左、R右分别表示Pk左、右两边荷载的合力。如果这一位置能使S有极大值,那么,不论荷载向左或向右移动时,都必然会使S减小,即ΔS<0。
首先使荷载向右移动Δx(设Δx以向右为正),则Pk将移动到影响线顶点之右。相应的影响线竖标改变量,在顶点之左为Δy1=Δxtanα,在顶点之右为Δy2=Δxtanβ,于是
ΔS1=R左Δy1+(Pk+R右)Δy2
=R左Δxtanα-(Pk+R右)Δxtanβ
=Δx[R左tanα-(Pk+R右)tanβ]<0
因为Δx为正值,则
R左tanα-(Pk+R右)tanβ<0 (a)
再将Pk置于影响线的顶点后,使荷载向左移动(-Δx)时,Pk将移动到影响线顶点之左,则
ΔS2=(R左+Pk)(-Δx)tanα-R右(-Δx)tanβ
=-Δx[(R左+Pk)tanα-R右tanβ]<0
所以 (Pk+R左)tanα-R右tanβ>0 (b)
将式(a)、式(b)中后项移项可得

由图9.5.4b可见
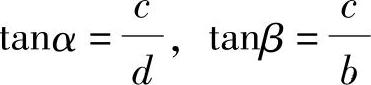
代入式(c)得

式(9.5.1)说明:如果把不等式的左边和右边分别视为a段和b段的平均荷载:则Pk计入影响线顶点的哪一边,这一边的平均荷载就较另一边的大,S将有极大值。荷载Pk就为临界荷载,与此相应的荷载位置,称为临界位置。由此可见,式(9.5.1)是判断Pk是否为临界荷载必须满足的条件,称为三角形影响线临界荷载判别式。
一般而言,给出一组移动荷载和量值S的影响线后,需根据式(9.5.1)选取若干个荷载试算,方能确定哪一个是临界荷载并从而定出最不利荷载位置。通常在数值较大、排列较密的那几个荷载中,出现临界荷载的可能性较大。有时临界荷载不止一个,这时可将相应极值分别算出,比较哪一个为最大,发生最大极值的那个荷载位置就是最不利位置。
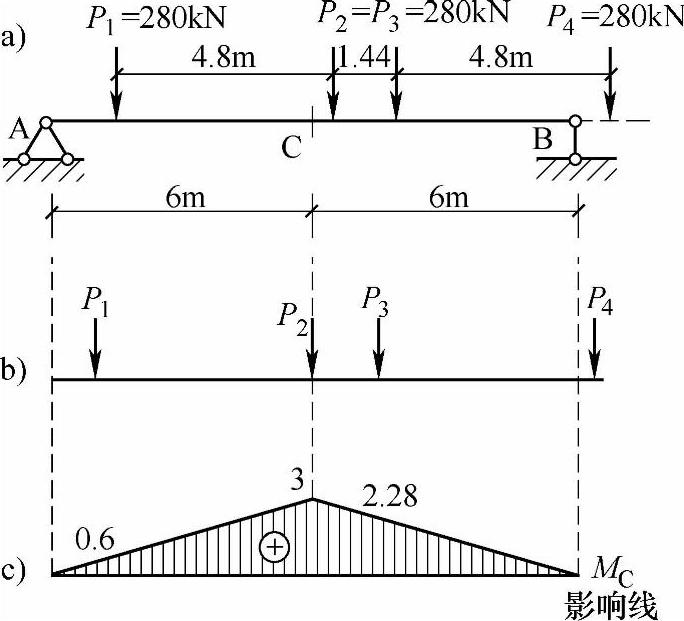
图 9.5.5
【9.5.2】 简支梁在吊车荷载作用下跨中截面的最大弯矩
条件:如图9.5.5a所示为一跨度12m的简支式吊车梁,同时有两台吊车在其上工作。
要求:试求跨中截面C的最大弯矩MCmax。
【解答】 (1)作MC影响线,如图9.5.5c所示。
(2)判别临界荷载。可以看出,当P2(或P3)位于影响线顶点(图9.5.5b)时,有较多的荷载位于顶点附近和梁上(注意P4已不在AB梁上),故可设P2(或P3)为Pk。由式(9.5.1)得
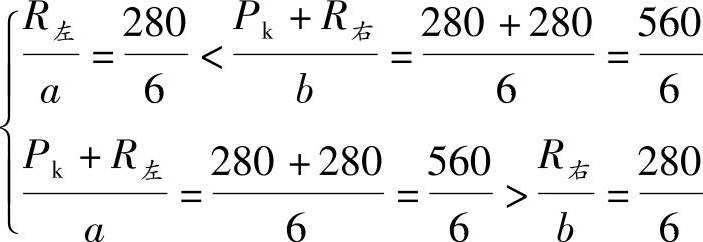
由计算结果可见,P2是临界荷载。
(3)计算MCmax。P1、P2、P3作用点处所对应的MC影响线上的竖标如图9.5.5c所示。
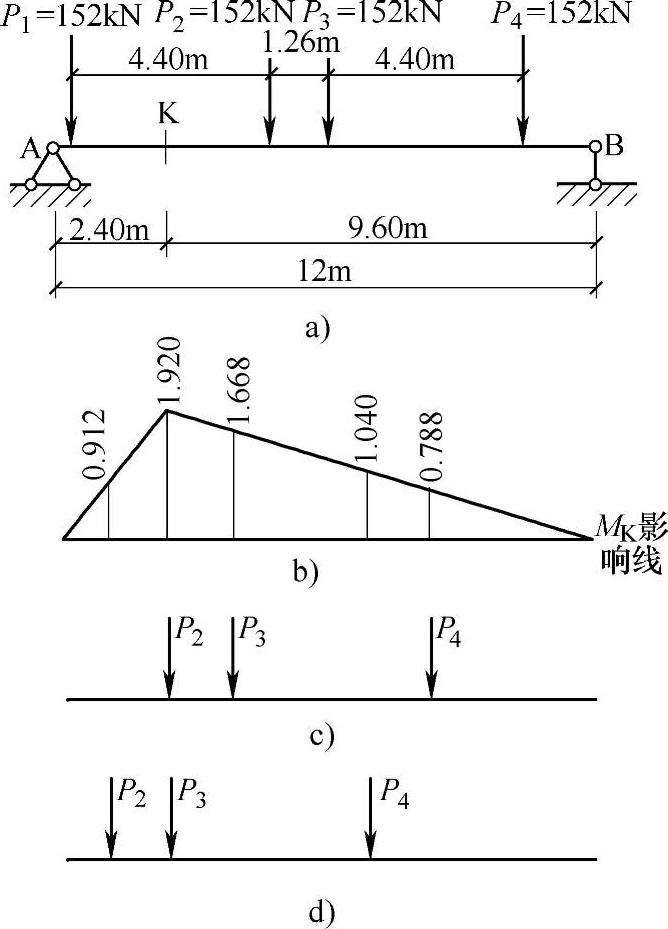
图 9.5.6
MCmax=P1y1+P2y2+P3y3
=280×(0.6+3+2.28)kN·m
=1646.4kN·m
P1、P4不是临界荷载(读者自行验算),将P3置于影响线顶点,可得出与上述同样的MC值,则此即为荷载最不利位置。
【9.5.3】 简支梁在吊车荷载作用下跨中某截面的最大弯矩
条件:如图9.5.6a所示简支梁,承受两台吊车的荷载。
要求:试求该简支梁在图示吊车荷载作用下截面K的最大弯矩。
【解答】 先作出MK的影响线,如图9.5.6b所示。
据前述推断,MK的最不利荷载位置将有如图9.5.6c、d所示两种可能情况。分别计算对应的MK值,并加以比较,即可得出MK的最大值。
对于图9.5.6c所示情况有
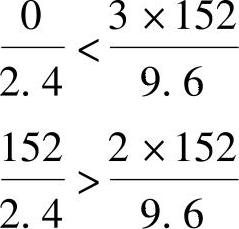
符合式(9.5.1)P2是临界荷载
MK=152×(1.920+1.668+0.788)=665.15kN·m
对于图9.5.6d所示情况有
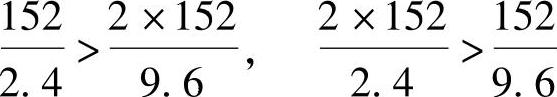
不符合不等式(9.5.1),P3不是临界荷载,即图9.5.6d不是一个临界荷载位置,则图9.5.6c所示即为MK的最不利荷载位置。此时
MKmax=665.15kN·m
【9.5.4】 两跨静定梁在吊车荷载作用下中间支座B的最大反力
条件:如图9.5.7a所示为吊车荷载作用下的两跨静定梁。
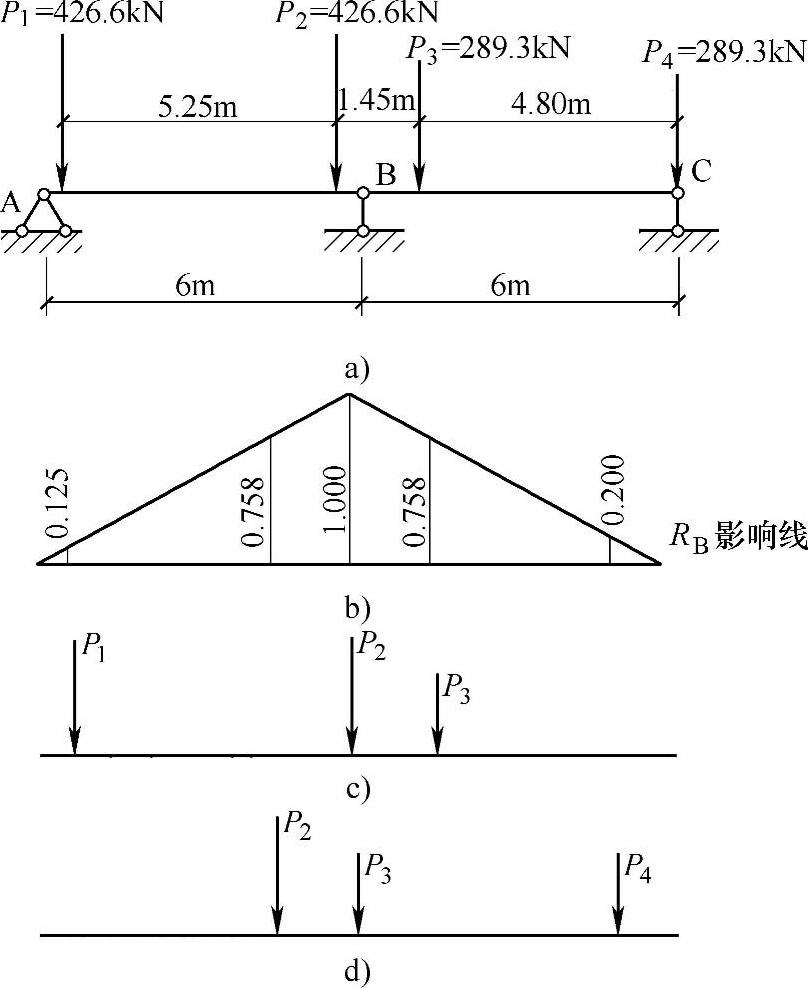
图 9.5.7
要求:试求支座B的最大反力。
【解答】 该梁实为两根简支梁,故可作出如图9.5.7b所示的RB影响线。其最不利荷载位置有如图9.5.7c、d所示两种可能情况,现分别计算如下。
考虑图9.5.7c所示情况有
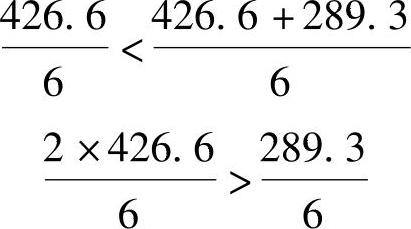
是一个临界荷载位置
RB=426.6×(0.125+1.000)+289.3×0.758=699.22kN
再考虑图9.5.7d所示情况有
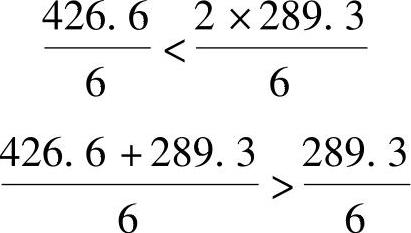
也是一个临界荷载位置
RB=426.6×0.758+289.3×(1.000+0.200)=670.52kN
二者比较可知,如图9.5.7c所示的荷载情况为最不利荷载位置,相应有RBmax=699.22kN。
真题 【9.5.5】~【9.5.7】 (2025年二级考题)
某楼面的均布活荷载为6kN/m2,该楼面结构中有一根钢筋混凝土连续梁,如图9.5.8所示。梁截面尺寸b×h=250mm×500mm。均布荷载标准值:静荷载(含自重)gk=20kN/m,活荷载qk=25kN/m。

图 9.5.8
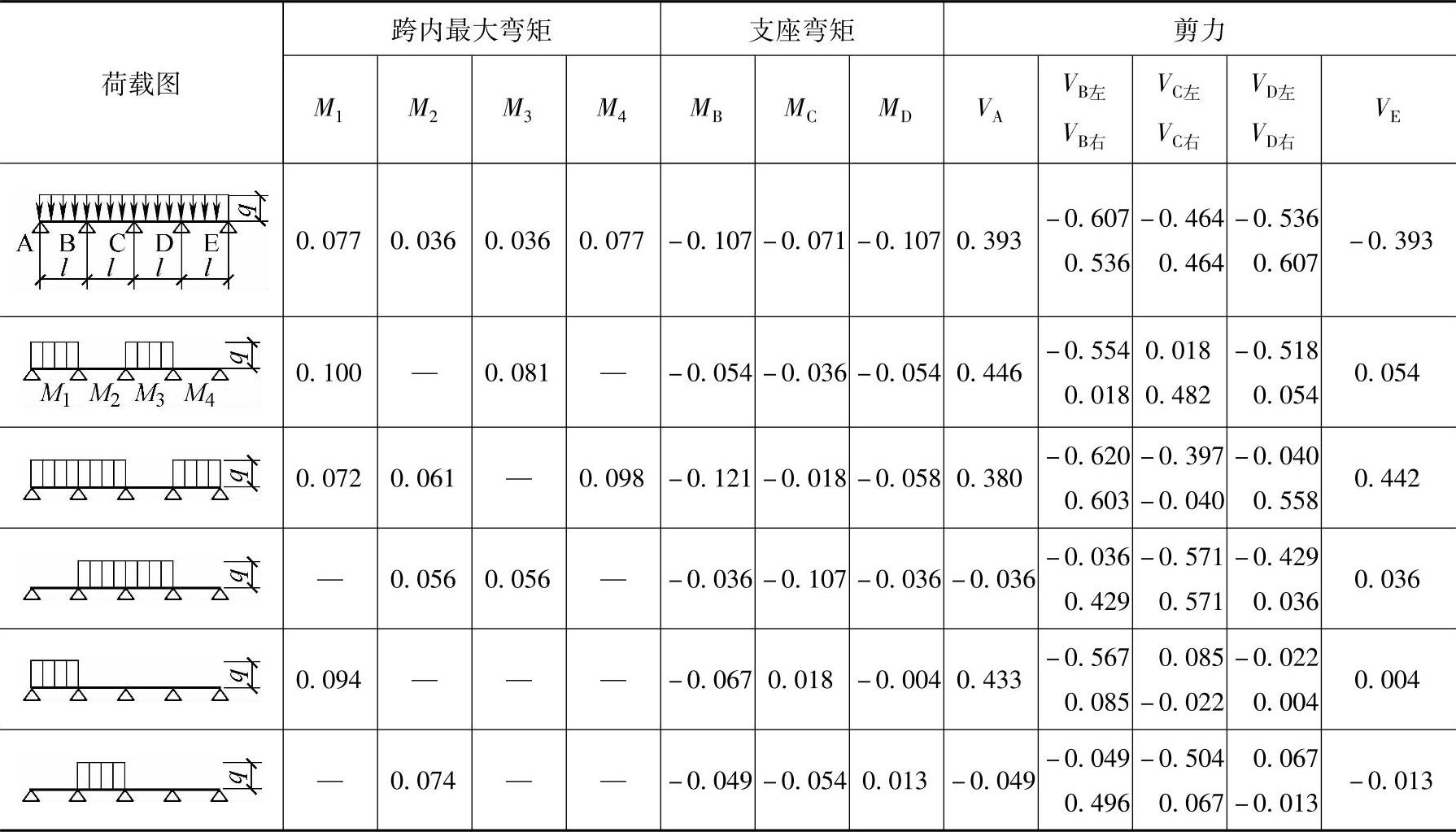
提示:计算梁内力时应考虑活荷载的不利布置,并按表9.5.1进行计算。
表9.5.1 连续梁内力系数表、弯矩M=表中系数×ql2、剪力V=表中系数×ql
真题 【9.5.5】 (2025年二级考题)
D支座截面的最大弯矩设计值MD与下列何项数值最为接近?
(A)-217.6kN·m (B)-234.0kN·m
(C)-227.3kN·m (D)-244.9kN·m
【答案】 (D)
【解答】 机动法作连续梁支座D的弯矩影响线,如图9.5.9所示,虚线为影响线形状,可以确定活荷载满布第1、3、4跨负号部分,可得支座负弯矩绝对值最大值。

图 9.5.9
连续梁系数表中没有直接对应的荷载布置,考虑结构对称,利用对称位置的荷载布置:第1、2、4跨满布时支座B负弯矩的绝对值最大值,即为所求。
根据《建筑结构荷载规范》3.2.3条及3.2.4条,最大弯矩设计值考虑由可变荷载效应控制的组合:
MD′=MB′=1.2×(-0.107)×gkl2+1.4×(-0.121)×qkl2
=-(1.2×0.107×20×62+1.4×0.121×25×62)
=-(92.448+152.46)=-244.91kN·m
由永久荷载效应控制的组合:
MD″=MB″=1.35×(-0.107)×gkl2+1.4×0.7×(-0.121)×qkl2
=-(1.35×0.107×20×62+1.4×0.7×0.121×25×62)
=-(104.004+106.722)=-210.73kN·m
比较二者,D支座截面最大弯矩设计值MDmax=-244.91kN·m
真题 【9.5.6】 (2025年二级考题)
DE跨跨中截面的最大弯矩设计值M4与下列何项数值最为接近?
(A)163.5kN·m (B)156.6kN·m (C)183.5kN·m (D)192.5kN·m
【答案】 (D)
【解答】 机动法作连续梁DE段跨中弯矩影响线如图9.5.10所示,虚线为影响线形状,可以确定活荷载满布第2、4跨正号部分,可得跨中弯矩最大值。
连续梁系数表中没有直接对应的荷载布置,考虑结构对称,利用对称位置的荷载布置:第1、3跨满布时第1跨跨中弯矩的最大值,即为所求。

图 9.5.10
根据《建筑结构荷载规范》3.2.3条及3.2.4条,最大弯矩设计值考虑
由可变荷载效应控制的组合:
M4′=M1′=1.2×0.077×gkl2+1.4×0.100×qkl2
=1.2×0.077×20×62+1.4×0.100×25×62
=66.528+126=192.53kN·m
由永久荷载效应控制的组合:
M4″=M1″=1.35×0.077×gkl2+1.4×0.7×0.100×qkl2
=1.35×0.077×20×62+1.4×0.7×0.100×25×62
=74.844+88.2=163.04kN·m
比较二者,DE跨中4截面最大弯矩设计值M4max=192.53kN·m
真题 【9.5.7】 (2025年二级考题)
在DE跨中靠近D支座截面的最大剪力设计值VD右,最接近下列何项数值?
(A)214.9kN (B)196.2kN (C)217.6kN (D)208.3kN
【答案】 (C)
【解答】 机动法作连续梁DE段靠近D支座截面,即支座D右侧截面的剪力影响线如图9.5.11所示,虚线为影响线形状,可以确定活荷载满布第1、3、4跨正号部分,可得剪力最大值。

图 9.5.11
连续梁系数表中没有直接对应的荷载布置,考虑结构对称,利用对称位置的荷载布置:第1、2、4、跨满布时B支座左侧截面的负号剪力绝对值最大值,即为所求。
根据《建筑结构荷载规范》3.2.3条及3.2.4条,最大剪力设计值考虑由可变荷载效应控制的组合:
V′D右=-V′B左=-[1.2×(-0.607)×gkl2+1.4×(-0.620)×qkl2]
=1.2×0.607×20×6+1.4×0.620×25×6(https://www.daowen.com)
=87.408+130.2=217.61kN
由永久荷载效应控制的组合:
V″D右=-V″B左=-[1.35×(-0.607)×gkl2+1.4×0.7×(-0.620)×qkl2]
=1.35×0.607×20×6+1.4×0.7×0.620×25×6
=98.334+91.14=189.47kN
比较二者,DE跨中靠近D支座截面最大剪力设计值VD右max=217.61kN
真题 【9.5.8】~【9.5.9】 (2025年二级考题)
某办公楼现浇钢筋混凝土三跨连续梁如图9.5.12所示。梁上作用的恒荷载标准值(含自重)gk=25kN/m,活荷载标准值qk=20kN/m。

图 9.5.12
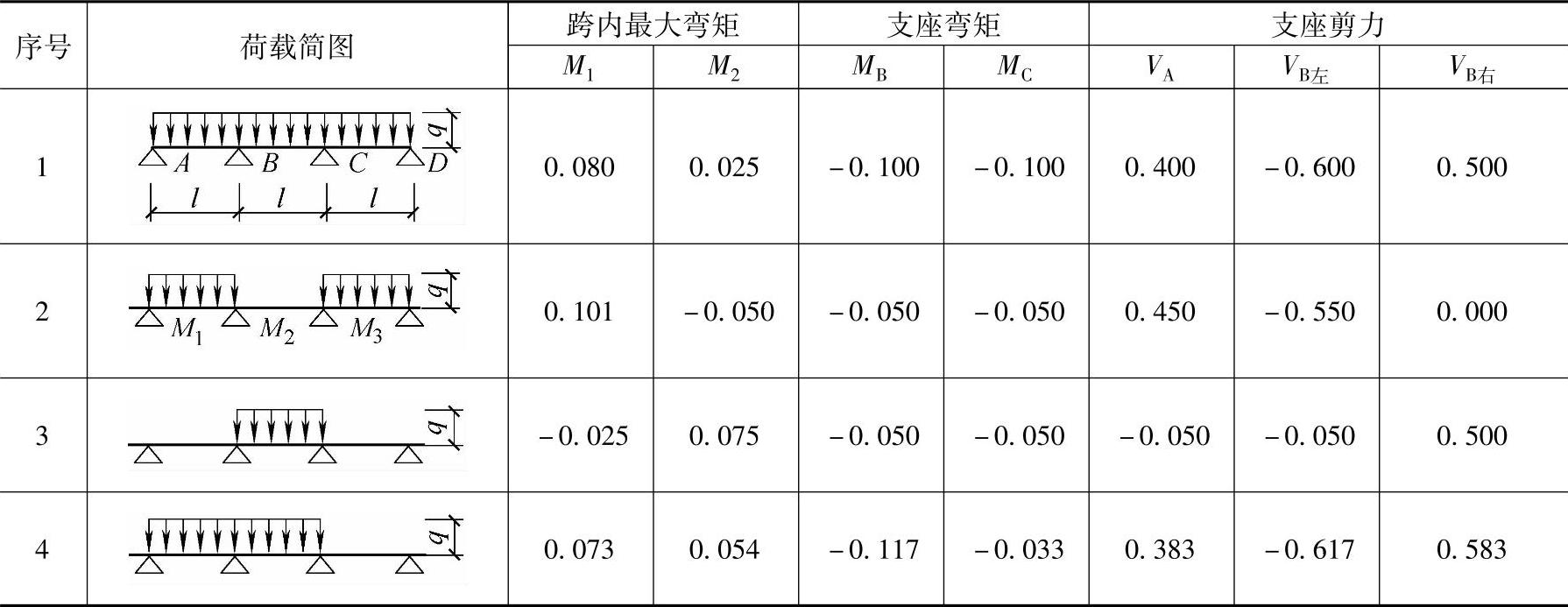
提示:计算梁内力时应考虑活荷载的不利布置,连续梁内力系数见表9.5.2。
表9.5.2 连续梁内力系数表(弯矩M=表中系数×ql2,剪力V=表中系数×ql)
真题 【9.5.8】 (2025年二级考题)
试问,该梁B支座截面的最大弯矩设计值MB(kN·m),与下列何项数值最为接近?
(A)251 (B)301 (C)325 (D)352

图 9.5.13
【答案】 (C)
【解答】 作该梁支座B的弯矩影响线如图9.5.13。
支座B的负弯矩绝对值最大时,应在1、2跨满布活荷载。
根据《建筑结构荷载规范》3.2.3条及3.2.4条,最大弯矩设计值考虑由可变荷载效应控制的组合:
MB′=1.2×(-0.100)×gkl2+1.4×(-0.117)×qkl2
=-(1.2×0.1×25×7.22)-(1.4×0.117×20×7.22)
=-155.52-169.83=-325.35kN·m由永久荷载效应控制的组合:
MB″=1.35×(-0.100)×gkl2+1.4×0.7×(-0.117)×qkl2
=-(1.35×0.1×25×7.2)2-(1.4×0.7×0.117×20×7.22)
=-174.96-118.881=-293.84kN·m
比较二者,B支座截面负弯矩绝对值最大弯矩MBmax=325.35kN·m
真题 【9.5.9】 (2025年二级考题)
试问,该梁BC跨靠近B支座截面的最大剪力设计值VB右(kN),与下列何项数值最为接近?
(A)226 (B)244 (C)254 (D)276
【答案】 (A)
【解答】 作该梁支座B右截面剪力影响线如图9.5.14所示。
BC跨靠近支座B截面的最大剪力设计值时,应在1、2跨的正号影响线满布活荷载。

图 9.5.14
根据《建筑结构荷载规范》3.2.3条及3.2.4条,最大剪力设计值考虑由可变荷载效应控制的组合:
V′B右=1.2×0.500×gkl+1.4×0.583×qkl2
=1.2×0.5×25×7.2+14×0.583×20×7.2
=108+117.53=225.53kN
由永久荷载效应控制的组合:
V″B右=1.35×0.500×gkl+1.4×0.7×0.583×qkl2
=1.35×0.5×25×7.2+1.4×0.7×0.583×20×7.2
=121.5+82.271=203.77kN
比较二者,BC跨中靠近B支座截面最大剪力设计值VB右max=225.53kN
真题 【9.5.10】 (2025年一级考题,原题为连锁题中的一道子题,现改写成一道独立题)
某多跨厂房,中列柱的柱距12m,采用钢吊车梁。在吊车梁上行驶两台重级工作制的软钩桥式吊车,起重量Q=50/10t,小车重g=16.6t,最大轮压标准值P=453.7kN,每台吊车的轮压分布如图9.5.15所示。
试问,由两台吊车垂直荷载产生的吊车梁支座处的最大剪力设计值(kN),应与下列何项数值最为接近?

图 9.5.15
(A)1616.0 (B)1516.2 (C)1191.3 (D)1083.0
【答案】 (A)
【解答】 题目为单跨简支梁,吊车竖向荷载作为行列荷载作用,求中间支座处剪力最大值。
(1)作单跨简支梁支座处的剪力影响线,与左支座的反力影响线图相同,如图9.5.16所示。作为一个斜率的影响线,荷载的最不利位置简单,可直接判断,吊车行列荷载较大、较密集的部分作用在影响线顶点附近,且一个集中力作用在顶点位置,注意此时行列荷载作用在梁上的个数和位置。
(2)根据吊车参数确定行列荷载的间距,放置在最不利位置,如图9.5.16所示。
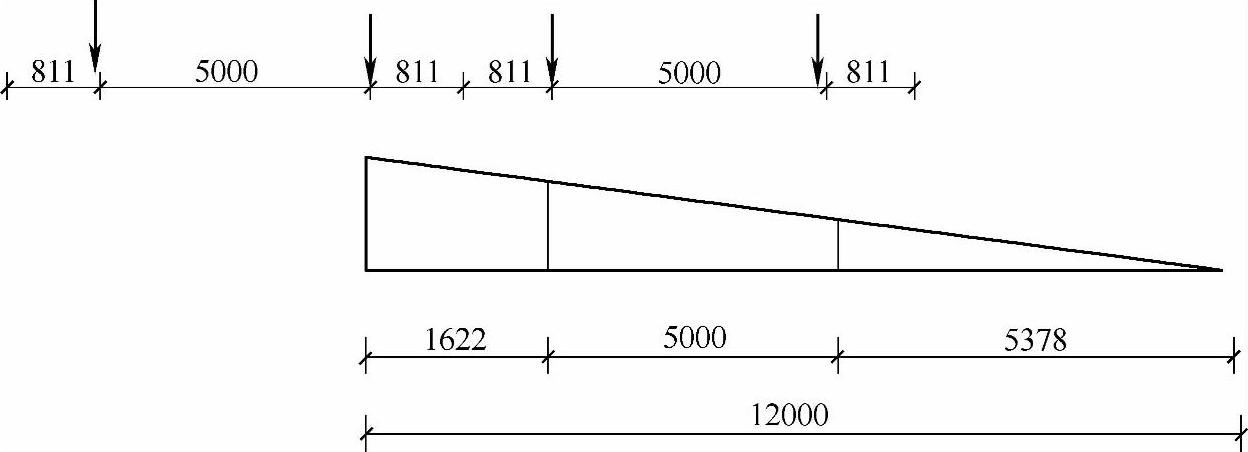
图 9.5.16
(3)荷载取最大轮压453.7kN计算。
(4)根据叠加原理计算:
根据《建筑结构荷载规范》3.2.4条、5.2.2条:分项系数1.4、动力系数1.1。
真题 【9.5.11】 (2025年一级考题,原题为连锁题中的一道子题,现改写成一道独立题)
某单层双跨等高钢筋混凝土柱厂房,其平面布置图、排架简图如图9.5.17所示。该厂房每跨各设有20/5t桥式软钩吊车两台,吊车工作级别为A6级,吊车参数见表9.5.3。
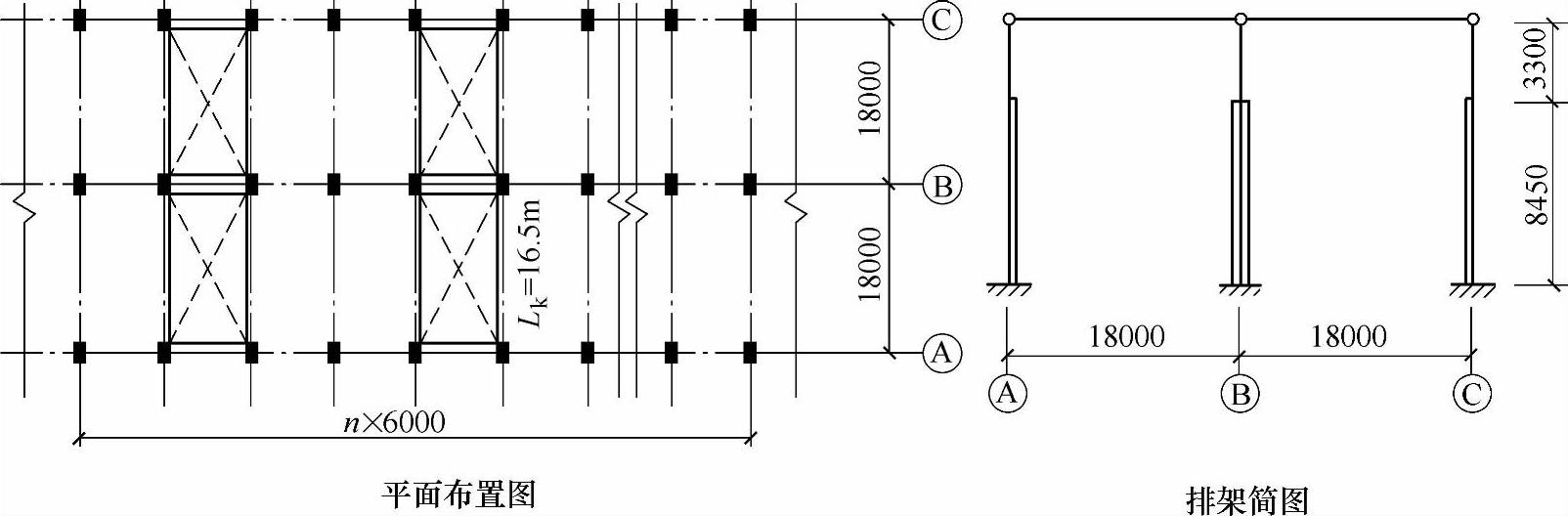
图 9.5.17
表9.5.3 吊车参数

试问,当进行仅有两台吊车参与组合的横向排架计算时,作用在边跨柱牛腿顶面的最大吊车竖向荷载(标准值)Dmax(kN)、最小吊车竖向荷载(标准值)Dmin(kN),分别与下列哪一组数值最为接近?
(A)178,43.7 (B)201.5,50.5 (C)324,80 (D)342,83.9
【答案】 (D)
【解答】 题目为两跨简支梁,吊车竖向荷载作为行列荷载作用,作用在边跨柱牛腿顶面的最大荷载引起最大的竖向反力,即求中间支座反力的最大值。
(1)作两跨简支梁中间支座的反力影响线如图9.5.18所示,布置吊车行列荷载,较大、较密集的部分作用在影响线顶点附近,且一个集中力作用在顶点位置。
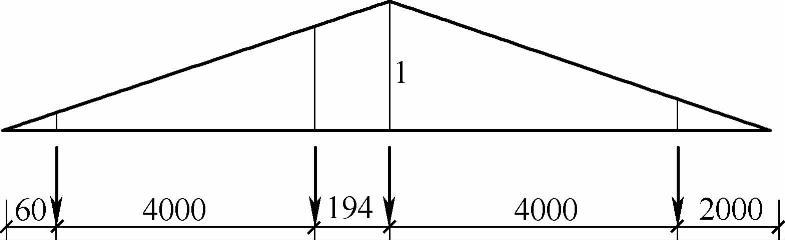
图 9.5.18
根据吊车参数确定行列荷载最不利位置。影响线与行列荷载排列,均对称,且荷载相等,只需要确定如图9.5.18所示的一种情况即可。
(2)考虑最大、最小吊车荷载情况,荷载分别取最大轮压178kN、最小轮压43.7kN计算。
(3)根据叠加原理计算:
根据《建筑结构荷载规范》表5.2.2条,2台吊车A6级,荷载折减系数为0.95。
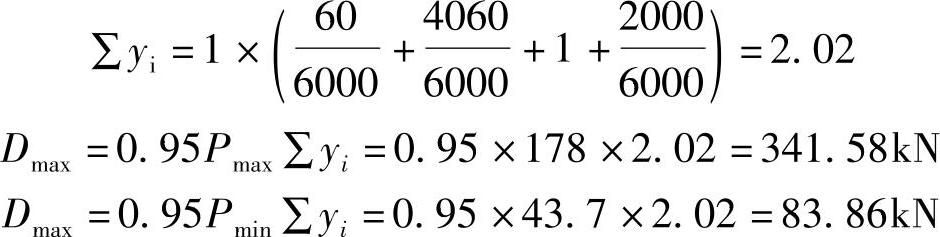
真题 【9.5.12】 (2025年一级考题,原题为连锁题中的一道子题,现改写成一道独立题)
某单层工业厂房为钢结构,厂房柱距21m,设置有两台重级工作制的软钩桥式吊车,吊车每侧有四个车轮,最大轮压标准值Pk,max=355kN。每台吊车的轮压分布如图9.5.19所示。图中长度单位为mm。
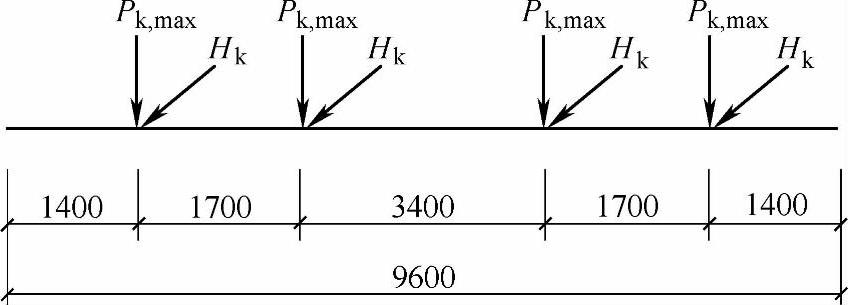
图 9.5.19
厂房排架分析时,假定两台吊车同时作用,试问,柱牛腿由吊车荷载引起的最大竖向反力标准值(kN),与下列何项数值最为接近?
(A)2913 (B)2191 (C)2081 (D)1972
【答案】 (C)
【解答】 题目为两跨简支梁,吊车竖向荷载作为行列荷载作用,求中间支座反力的最大值。
(1)作两跨简支梁中间支座的反力影响线如图9.5.20所示,布置吊车行列荷载,较大、较密集的部分作用在影响线顶点附近,且一个集中力作用在顶点位置。
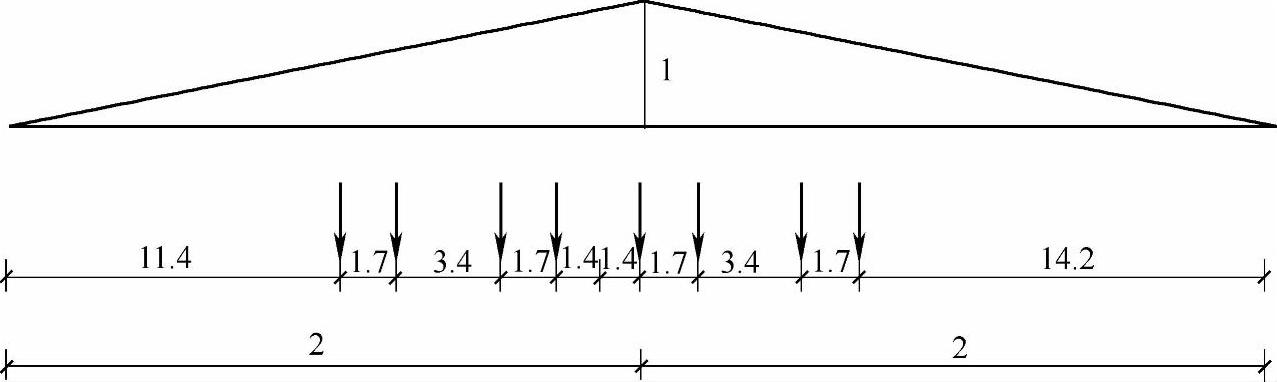
图 9.5.20
(2)根据吊车参数确定行列荷载最不利位置。影响线与行列荷载排列均对称,且荷载相等,只需要确定如图9.5.20所示一种情况即可。
(3)考虑最大值,荷载取最大轮压355kN计算。
(4)根据叠加原理计算:
根据《建筑结构荷载规范》表5.2.2条,2台吊车重级应为A6-A8级,荷载折减系数为0.95。
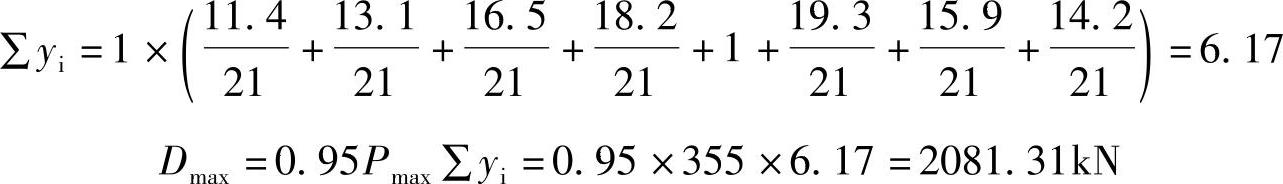
真题 【9.5.13】 (2025年一级考题)
一级公路上的一座桥梁,主桥为三跨(70m+100m+70m)变截面预应力混凝土连续箱形截面梁,如图9.5.21所示;试问,该桥用车道荷载求边跨(L1)跨中正弯矩最大值时,车道荷载顺桥向布置,下列哪种布置符合规范规定?
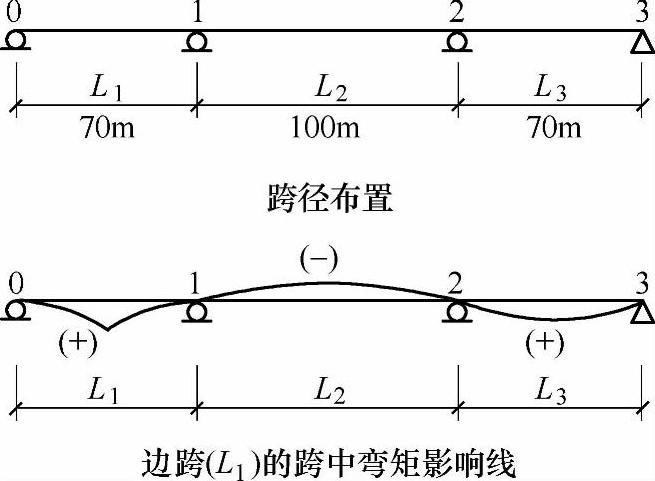
图 9.5.21
提示:三跨连续梁的边跨(L1)跨中影响线如图9.5.21所示。
(A)三跨都布置均布荷载和集中荷载
(B)只在两边跨(L1和L3)内布置均布荷载,并只在L1跨最大影响线坐标值处布置集中荷
载
(C)只在中间跨(L2)布置均布荷载和集中荷载
(D)三跨都布置均布荷载
【答案】 (B)
【解答】 《公路桥涵设计通用规范》4.3.1条4款3项规定:“车道荷载的均布荷载标准值应满布于使结构产生最不利效应的同号影响线上;集中荷载标准值只作用于相应影响线中一个最大影响线峰值处”。根据上述规定,(A)、(C)、(D)三种荷载布置都不会使边跨(L1)的跨中产生最大正弯矩,只有(B)种布置才能使要求截面的弯矩产生最不利效应,而且(C)种布置甚至使边跨相应截面产生负弯矩。所以说,该题正确答案应该是(B)。
真题 【9.5.14】 (2025年一级考题,因《规范》改版,故本题有关参数作了相应调整)
某公路桥梁,计算跨径为L=24.2m,由双车道和人行道组成。桥面宽度为0.25m(栏杆)+1.5m(人行道)+7.0m(车行道)+1.5m(人行道)+0.25m(栏杆)=10.5m。桥梁结构由梁高1.5m的5根T形截面主梁和5根横梁组成。桥梁结构的布置如图9.5.22所示。设计荷载为公路-Ⅰ级车道荷载。
试问,该桥主梁跨中断面由两行汽车荷载引起的总弯矩值与下列何项数值最为接近?
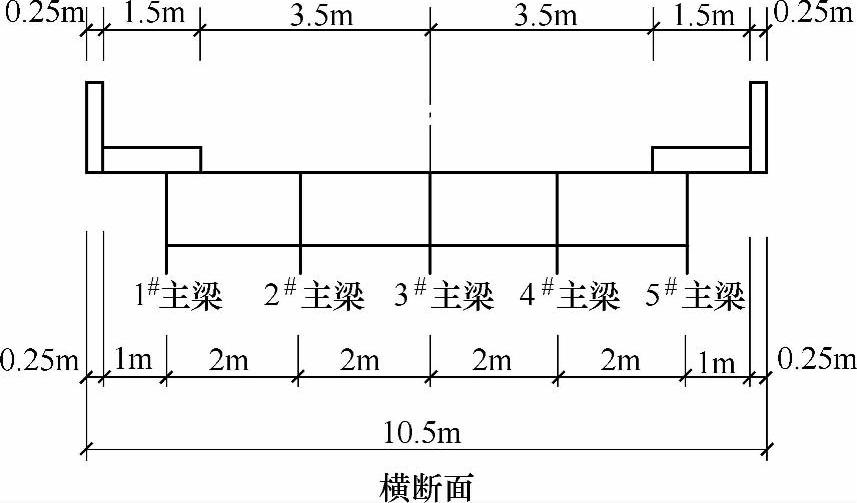
图 9.5.22
提示:不计冲击系数与横向分布系数。
(A)2404.0kN·m (B)2526.0kN·m
(C)2322.3kN·m (D)2236.5kN·m
【答案】 (C)
【解答】 (1)根据《公路桥涵设计通用规范》4.3.1条4款,计算跨径24.2m的公路-Ⅰ级车道荷载,均布荷载:qk=10.5kN/m
集中荷载: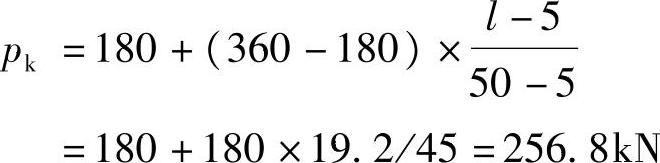
(2)影响线。跨中弯矩影响线的最大纵标
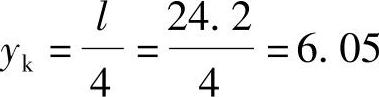
跨中弯矩影响线的面积
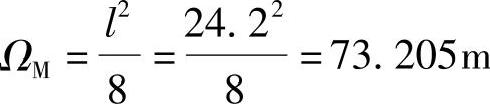
(3)跨中汽车荷载引起的弯矩值
Mq=Pkyk+qkΩ=256.8×6.05+10.5×73.205
=2322.293kN·m
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








