（一）长度不定可以任意布置的均布荷载

如果移动荷载是均布荷载，而且它可以任意断续布置，其分布长度也可以是任意的（例如人群等活荷载），则荷载的最不利位置易于由观察确定，由式（9.4.2）

可知，当荷载布满影响线正号部分时，S有最大值S_max；当荷载布满影响线负号部分时，S有最小值S_min。例如图9.5.1a所示外伸梁，由截面C的弯矩影响线图9.5.1b可知，当均布荷载布满梁的AB段（图9.5.1c）时，M_C为最大值M_Cmax；当均布荷载布满梁的AD段和BE段（图9.5.1d）时，M_C为最小值M_Cmin。

（二）定长的均布荷载

公路桥涵设计中最常见的具有一定长度的均布荷载，如履带式拖拉机。这里讨论影响线为三角形的情况。显然，为使所研究的量值达到最大，应使均布荷载范围对应的影响线面积ω最大。

可以证明，将均布荷载置于两端点对应的影响线纵距（y_a和y_b）恰好相等的地方ω达最大。如图9.5.2所示的荷载位置正是它的最不利荷载位置。

【9.5.1】 用影响线求多跨静定梁某截面在均布荷载作用下的正、负（绝对值）最大弯矩。

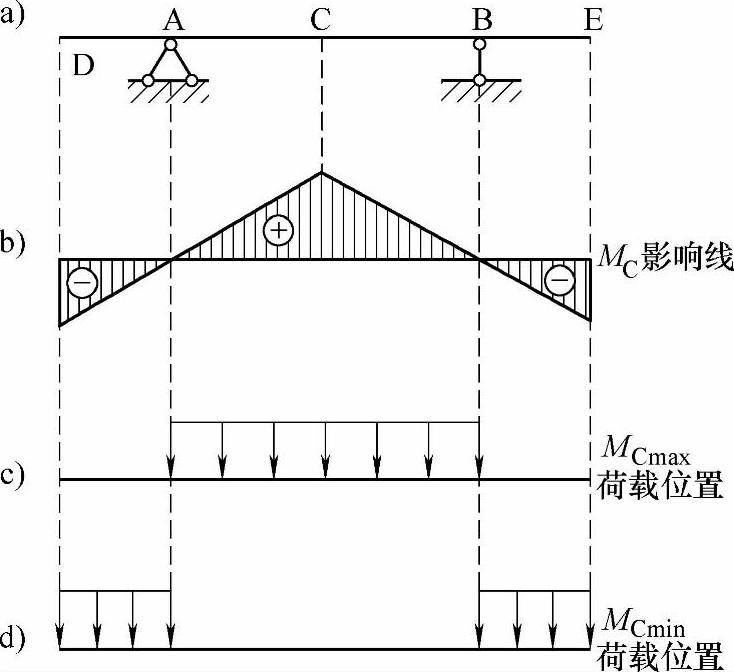
图 9.5.1

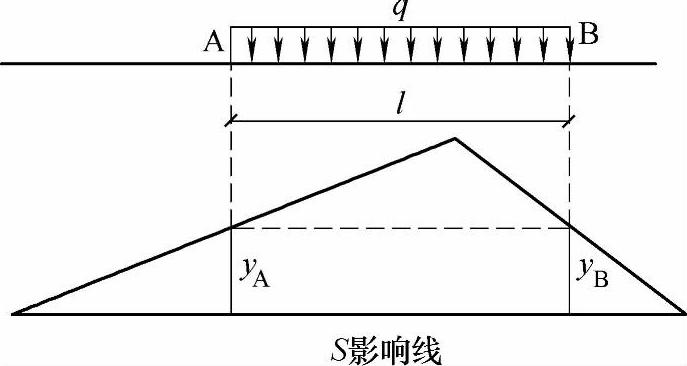
图 9.5.2

条件：如图9.5.3a所示多跨静定梁承受满跨固定均布荷载q₁和可以任意布置的可动均布荷载q₂作用，已知q₁=10kN/m，q₂=15kN/m。(www.daowen.com)

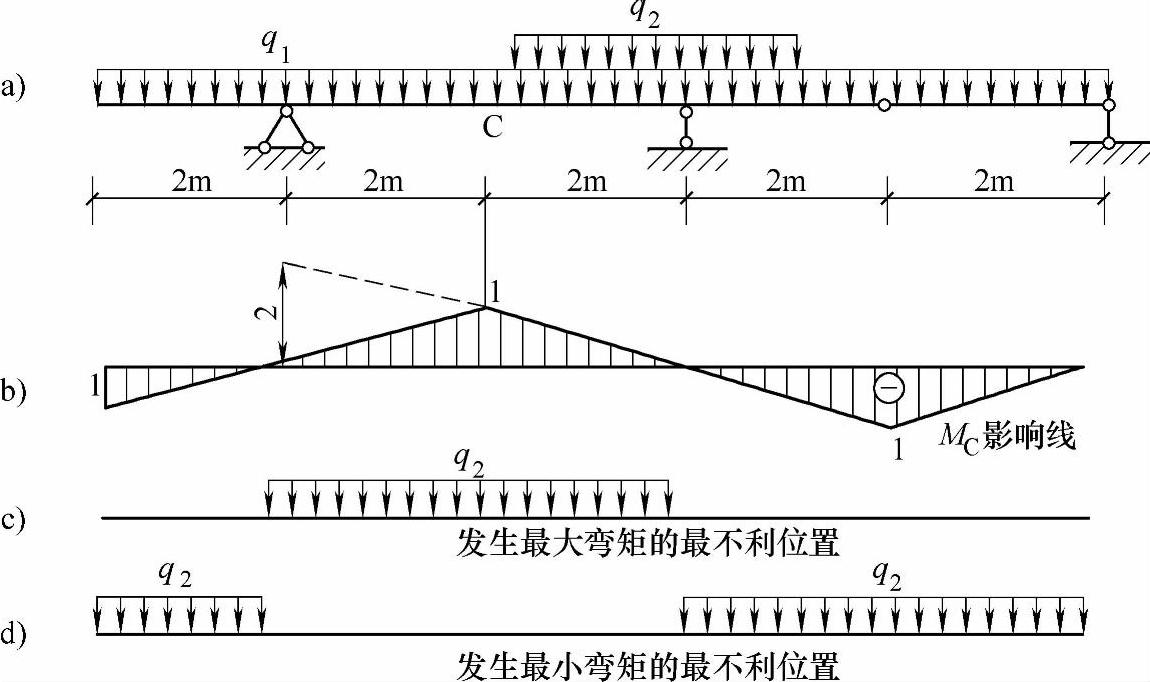
图 9.5.3

要求：计算截面C的最大弯矩和最小弯矩（绝对值最大负弯矩）。

【解答】 作M_C影响线如图9.5.3b所示，固定均布荷载q₁可布满梁的全长，因此它产生的M_Cq1等于M_C影响线的各部分面积的代数和乘以q₁，即

为使截面C产生最大弯矩，可动均布荷载q₂的布置应如图9.5.3c所示，此时q₂产生的M′_Cq2为

为使截面C产生最小弯矩（绝对值最大负弯矩），可动均布荷载q₂的布置应如图9.5.3d所示，此时q₂产生的M″_Cq2为

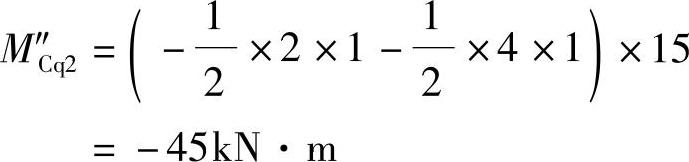
根据叠加原理，可得M_Cmax和M_Cmin如下：

M_Cmax=M_Cq1+M′_Cq2=-10+30=20kN·m

M_Cmin=M_Cq1+M″_Cq2=-10-45=-55kN·m