简支梁的支座反力和任一截面的弯矩、剪力的影响线是最基本、最常用的影响线，用静力法作简支梁反力和内力（弯矩和剪力）影响线的方法。是以单位荷载的作用位置x为自变量，根据隔离体平衡条件列出所求内力、支座反力的影响线方程，依此画出影响线。注意，影响线方程往往分段列出。列影响线方程时要注意坐标的选择，因为坐标的选择与计算的繁简程度有较大关系。

（一）支座反力影响线

简支梁支座反力R_A的影响线。

将P=1放在简支梁上任意位置，距A为x。由∑M_B=0，得

这就是R_A的影响线方程，是一条直线。

当x=0时，R_A=1

当x=l时，R_A=0

画出R_A的影响线，如图9.2.1c所示。它的纵距是无名数。

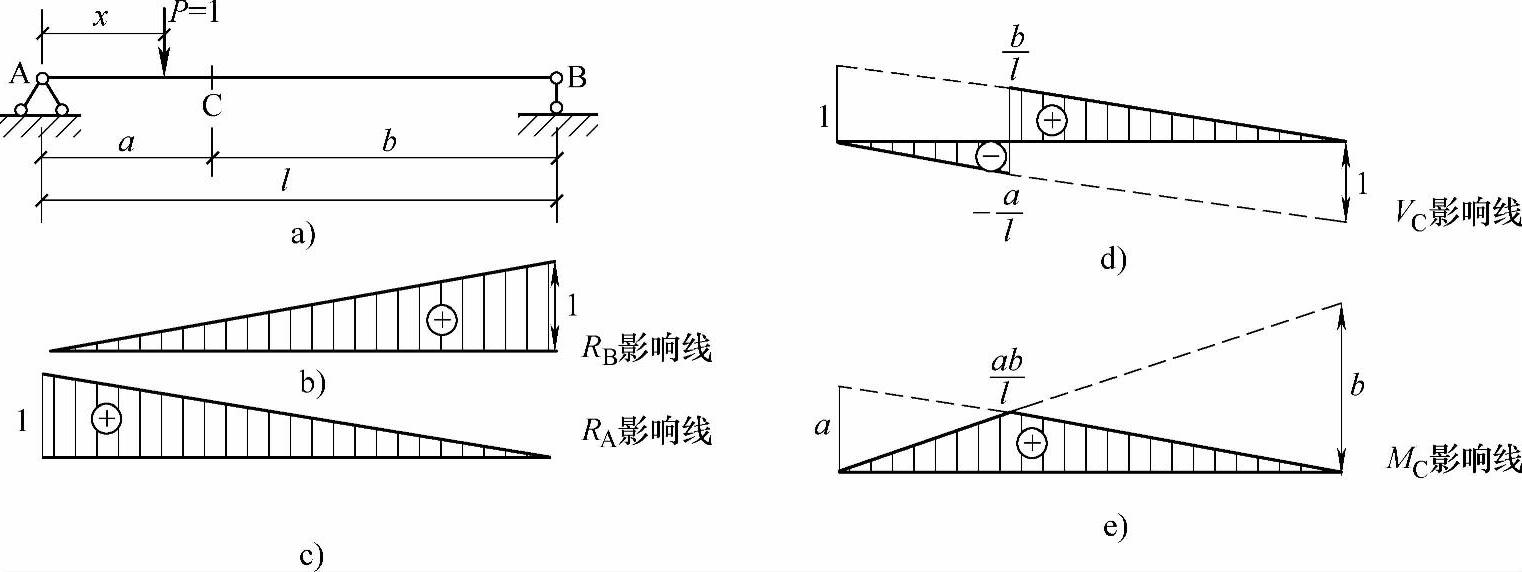
图 9.2.1

（二）剪力影响线

绘制指定截面C的剪力V_C的影响线。当P=1在截面C以左或以右移动时，剪力V_C的方程不同，故应以截面C为界分成左右两段考虑。

当P=1作用在AC段时，则取截面C的右边为隔离体，由∑Y=0，得

V_C=-R_B （P=1在AC段）

在AC段内，V_C的影响线与R_B的影响线相同，但正负号相反。因此，可先把R_B的影响线画在基线下面，保留AC段。C点的纵距按比例关系求得为。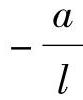

当P=1作用在CB段时，我们取截面C的左边为隔离体，由∑Y=0，得

V_C=R_A （P=1在CB段）

由此看出，在CB段内，V_C的影响线与R_A的影响线相同。因此，可先作R_A的影响线，然后保留其中的CB段（AC段舍弃不用）。C点的纵距可按比例关系求得为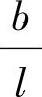。V_C影响线如图9.2.1d所示。(www.daowen.com)

由上可知，V_C的影响线由两段相互平行的直线组成，纵距在C点有一个突变，其值为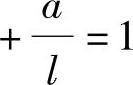。当P=1作用在AC段任一点时，截面C为负号剪力。当P=1作用在CB段任一点时，截面C为正号剪力。当P=1正好作用在C点时，V_C的影响值没有意义。

剪力影响线的纵距和反力的一样，也是无名数。

（三）弯矩影响线

绘制指定截面C的弯矩M_C的影响线，也要分成左右两段考虑。

当P=1作用在CB段时，取截面C的左边为隔离体，得

M_C=R_Aa （P=1在CB段）

由此看出，在CB段内，M_C的影响线纵距等于R_A的影响线纵距的a倍（a是截面C到支座A的距离）。因此，可以把R_A影响线的纵距乘以a，然后保留其中的CB段，就得到M_C在CB段的影响线。

当P=1作用在AC段时，取截面C的右边为隔离体，得

M_C=R_Bb （P=1在AC段）

因此，可先把R_B的影响线的纵距乘以b（b是截面C到支座B的距离），然后保留其中的AC段，就得到M_C在AC段的影响线。

由上可知，M_C的影响线分成AC和CB两段直线，形成一个三角形，如图9.2.1e所示。这里C点的纵距应为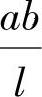，M_C的影响线纵距都是正的。

弯矩影响线纵距的单位为长度单位。

学习时，应注意影响线与内力图是两个完全不同的概念，千万不要混淆。

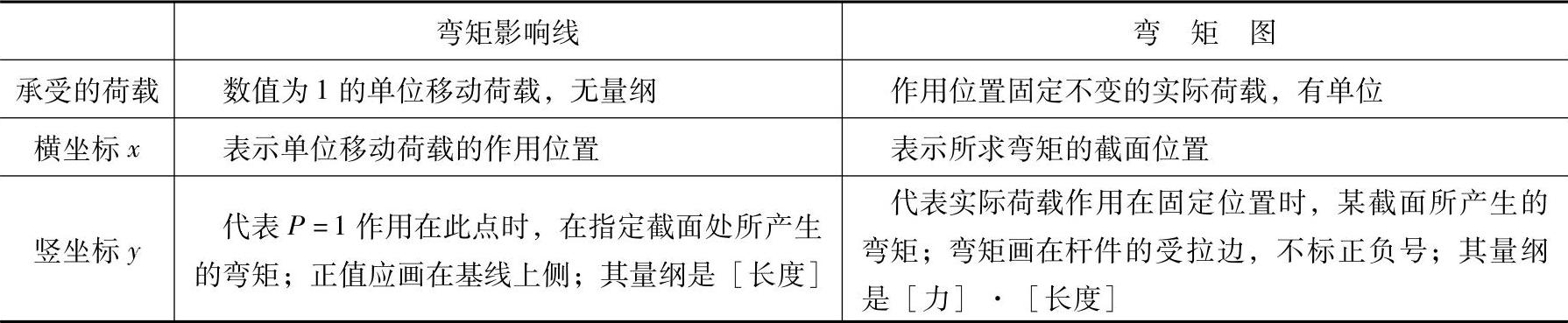
图9.2.2a、b分别是简支梁AB的弯矩影响线和弯矩图，这两个图形的形状虽然相似，但其概念却完全不同。表9.2.1把两个图形的主要区别加以比较，以便更好地掌握影响线的概念。

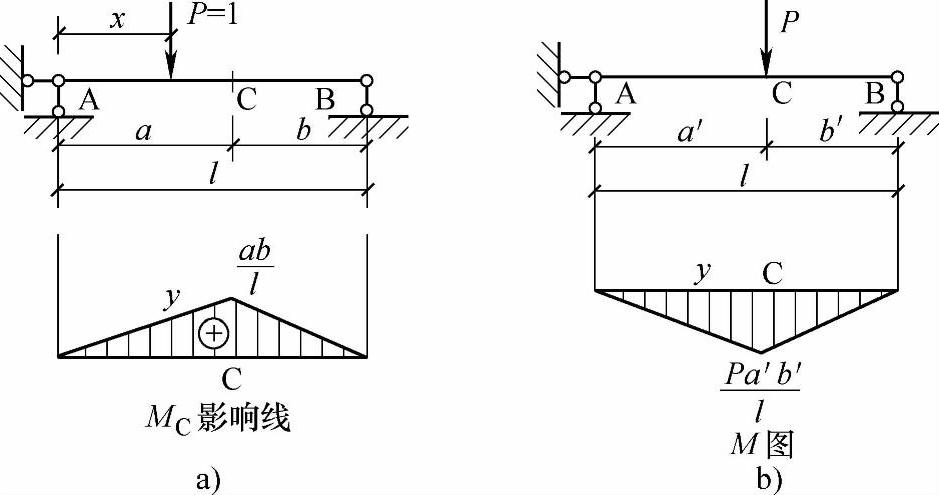
图 9.2.2

表 9.2.1