
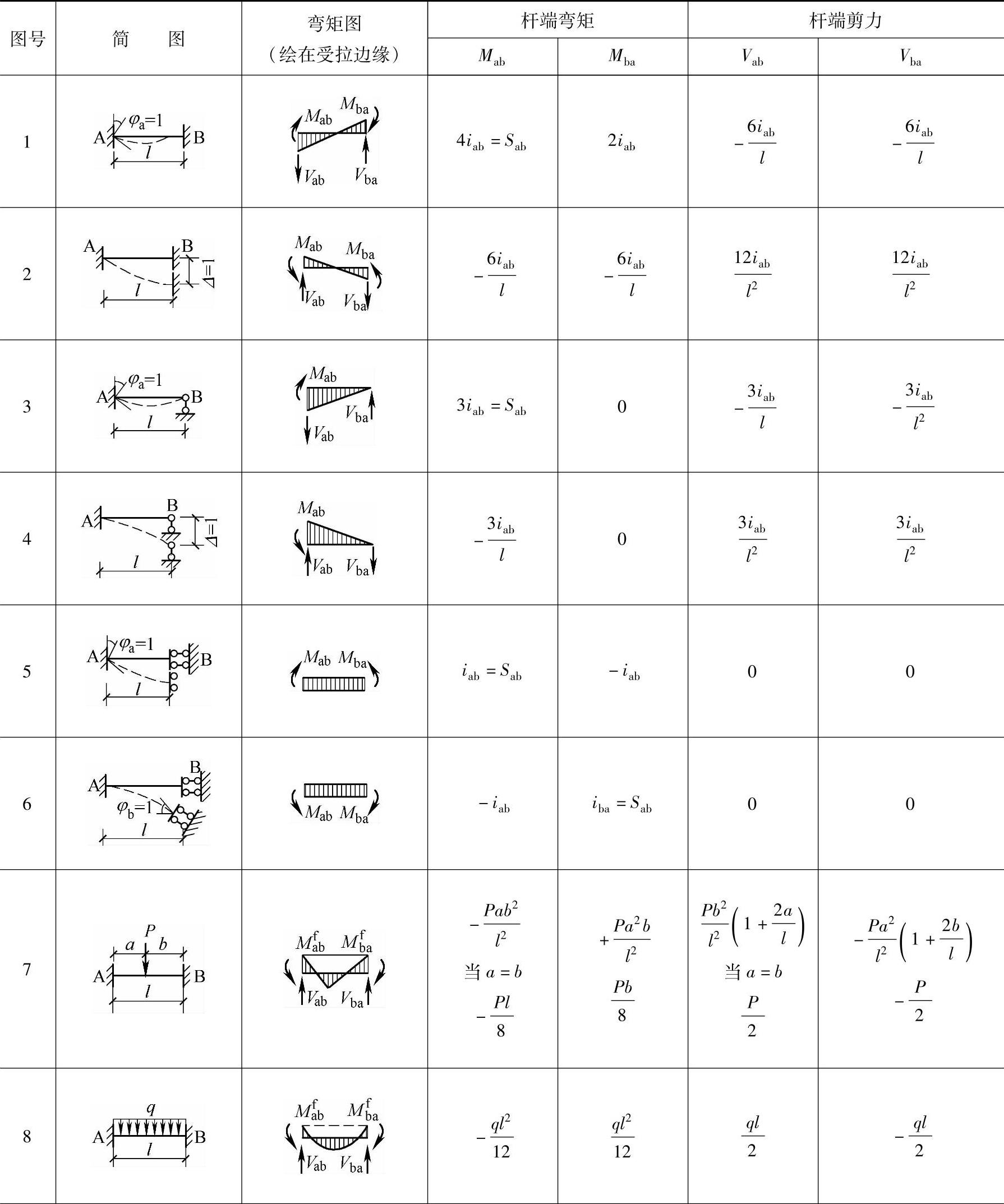
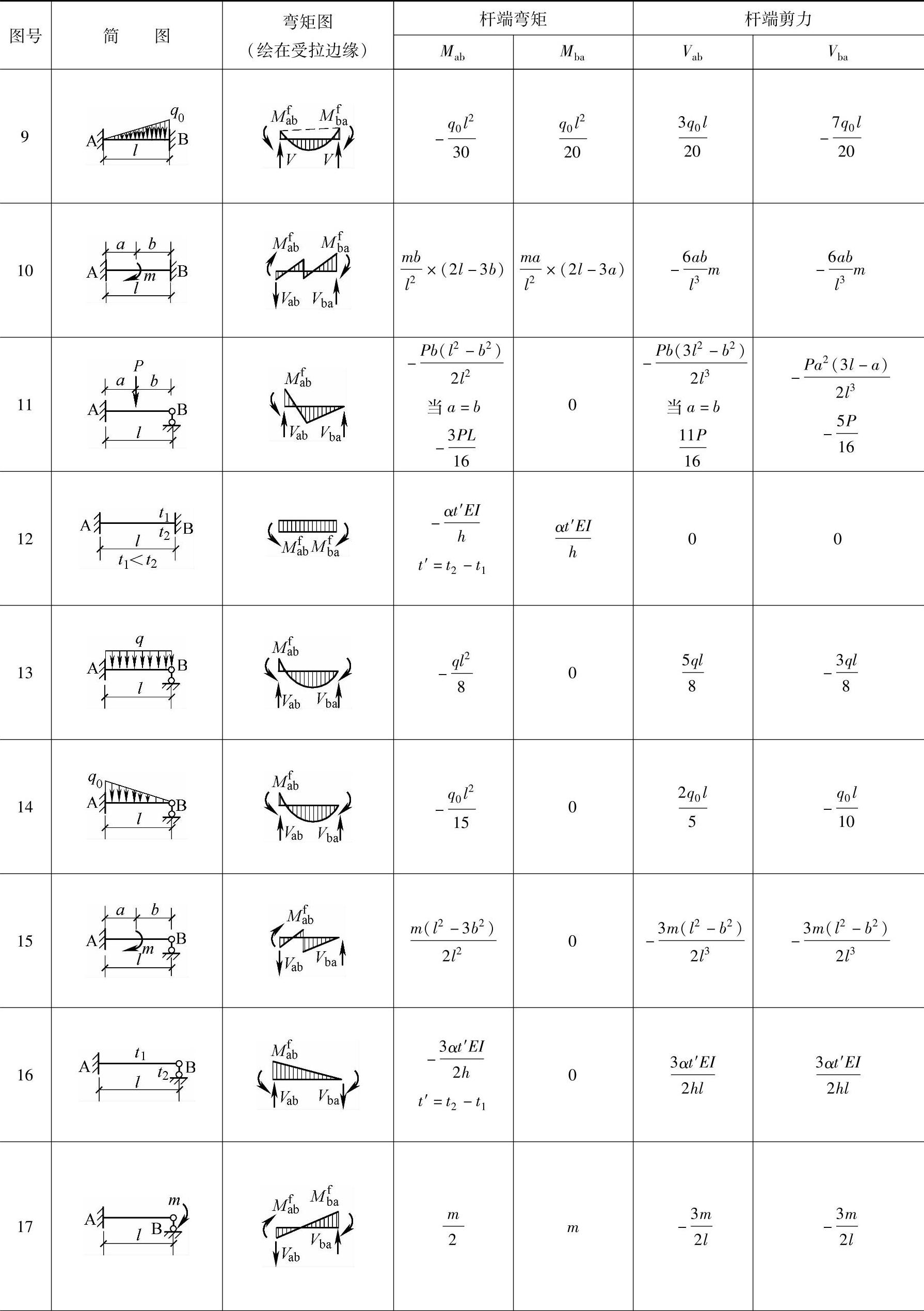
由杆端位移及各种荷载情况引起的等截面单跨超静定梁的固端弯矩和剪力可以从表7.2.1中查到。
表7.2.1 等截面单跨超静定梁杆端形常数、载常数表iab=EI/lab
(续)
(续)
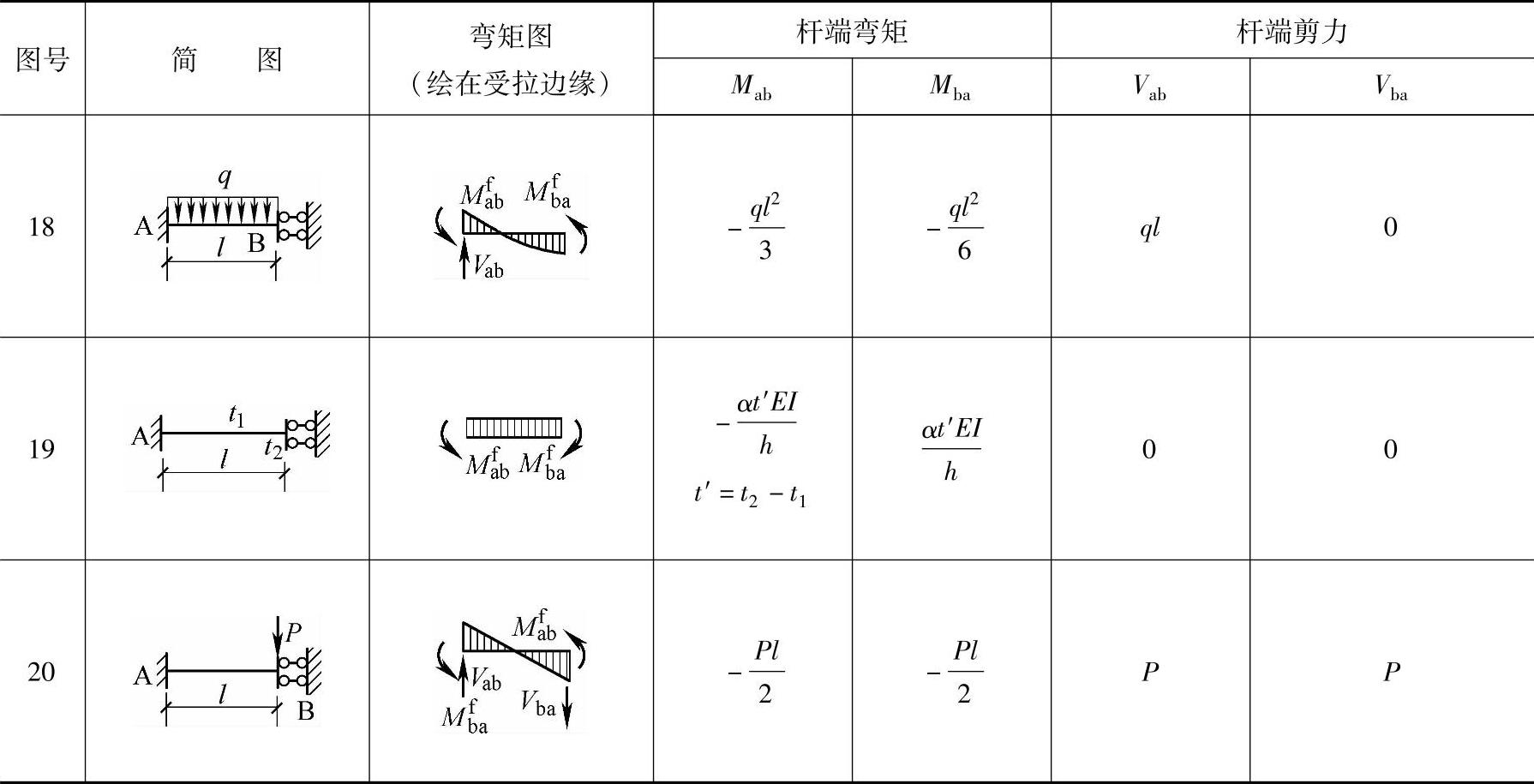
注:杆端弯矩栏中的符号是根据以顺时针为正的规定而加上去的;剪力符号规定同前。
查表时注意以下三点:
1)杆端转角以顺时针为正,杆端相对线位移以使其弦转角顺时针为正,反之为负。当杆端位移为负时相应的杆端弯矩也要改变符号。
2)杆端弯矩以顺时针为正,剪力以使其所在截面顺时针转为正。
3)求载常数时,当杆端支座情况与表上所示A、B端支承情况互调时,则A、B端的固端内力值相互调换并且还须改变一个符号。
【7.2.1】 二跨连续梁的内力计算
条件:如图7.2.3a所示连续梁。
要求:利用力矩分配法求解各杆的弯矩并绘弯矩图。
【解答】 (1)先在节点B加一附加刚臂如图7.2.3b所示,使节点B不能转动,即锁住。此时各杆端产生的固端弯矩由表7.2.1求得:
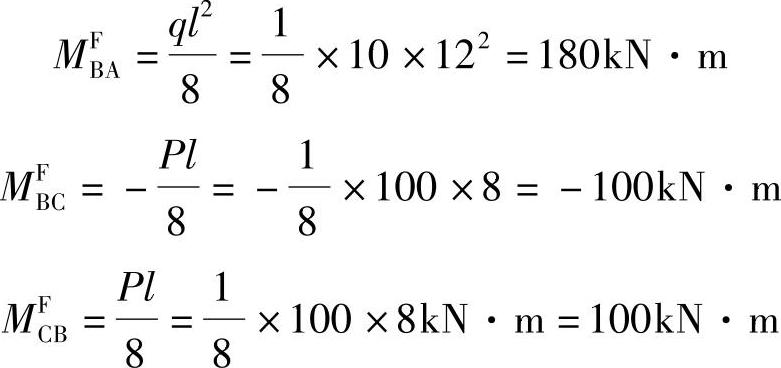
由节点B的平衡条件∑MB=0求得约束力矩
MFB=MFBA+MFBC=(180-100)kN·m=80kN·m
(2)为了消除约束力矩MB,应在节点B处加入一个与它大小相等方向相反的力矩-MB(图7.2.3c各杆端进行分配和传递),在-MB作用下节点B转动到无附加约束时的自然位置,即“放松节点”。将图7.2.3b和图7.2.3c相叠加就得到图7.2.3e中的结果。对于图7.2.3c,我们可用上述力矩分配法的基本运算求出各杆端的分配与传递弯矩。
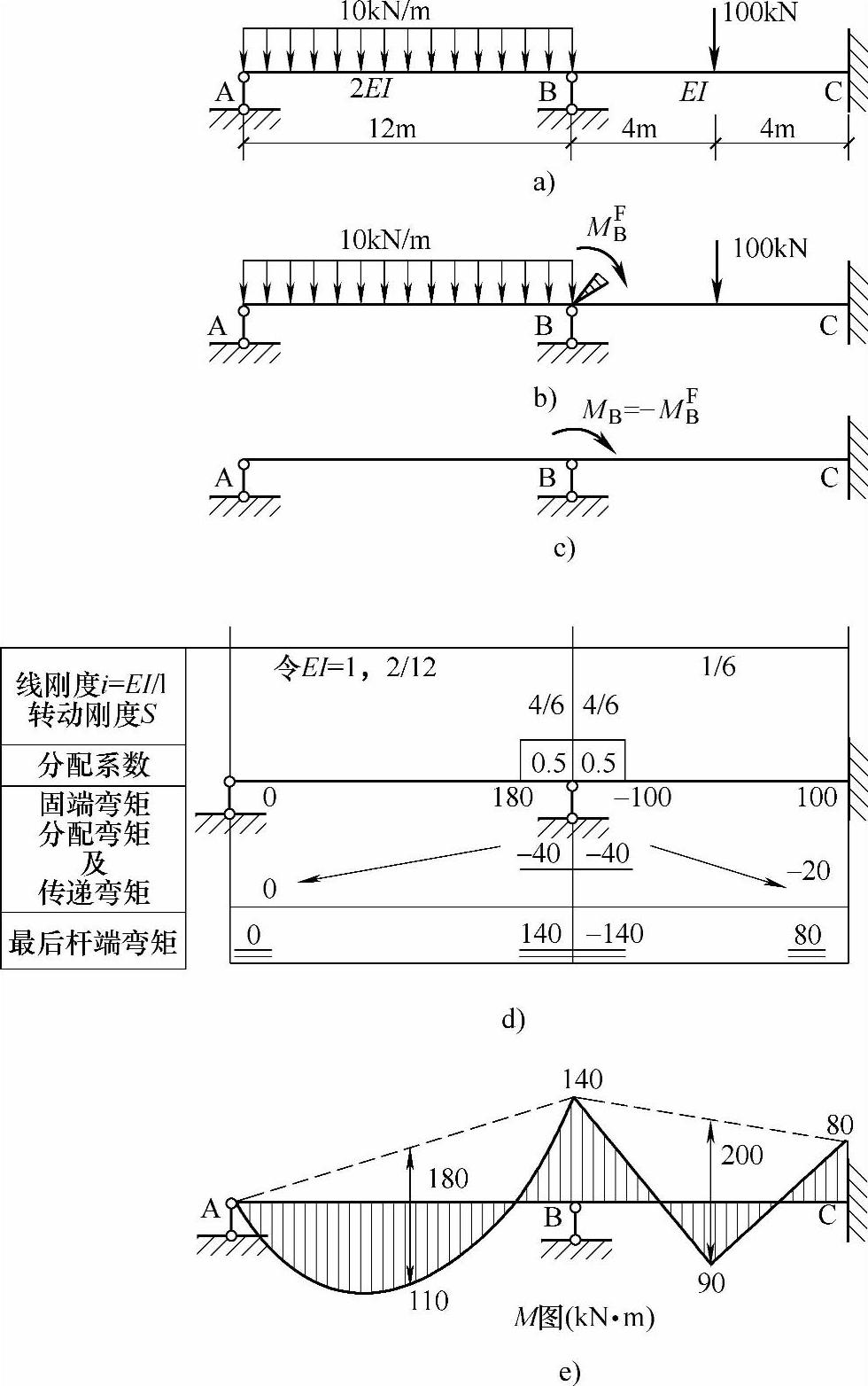
图 7.2.3
为此,先按式(7.2.2)算出各杆端分配系数
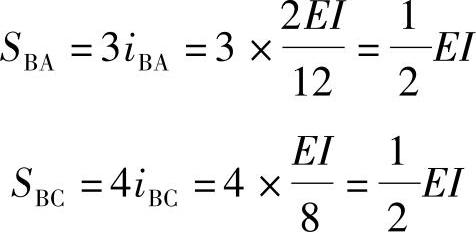
则
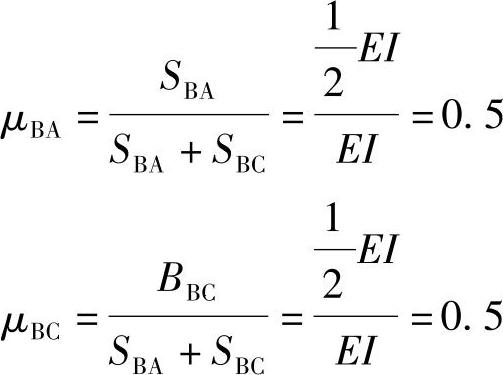
利用公式∑μ1k=1进行校核:∑μBk=μBA+μBC=0.5+0.5=1
所以分配系数计算正确。
根据公式(7.2.1)计算各杆近端的分配弯矩
MμBA=μBAMB=0.5×(-80)kN·m
=-40kN·m
MμBC=μBCMB=0.5×(-80)kN·m
=-40kN·m
然后计算各杆远端的传递弯矩
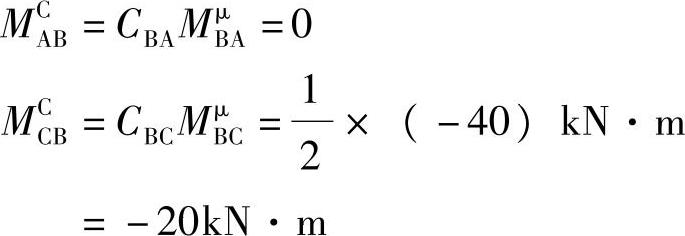
(3)最后将各杆端的固端弯矩(图7.2.3b)与分配弯矩、传递弯矩(图7.2.3c)相加,即得各杆端的最后弯矩值
MAB=MFAB+MCAB=0
MBA=MFBA+MμAB=(180-40)kN·m=140kN·m
MBC=MFBC+MμBC=(-100-40)kN·m=-140kN·m
MCB=MFCB+MCCB=(100-20)kN·m=80kN·m
为了计算方便,实际计算时,可以将线刚度、转动刚度及分配系数和固端弯矩的计算,以及分配弯矩、传递弯矩和最后杆端弯矩的计算用图7.2.3d的形式表示。表中各杆端弯矩的正负号以对杆端顺时针转动方向为正,表中弯矩的单位为kN·m。表中分配弯矩下面画一横线,表示该节点已经平衡。箭头表示弯矩的传递方向。杆端弯矩的最后结果下面画双横线。
用区段叠加法画出弯矩图如图7.2.3e所示。注意弯矩竖标画在受拉一侧。
真题 【7.2.2】 (1999年一级考题)
有一等截面的钢筋混凝土梁,受某种工况荷载(设计值)的作用,如图7.2.4所示。该梁矩形截面b×h(mm2)、钢筋及混凝土材料已定,按单筋梁配置。试问B支座的配筋量As应为下列何项所示?
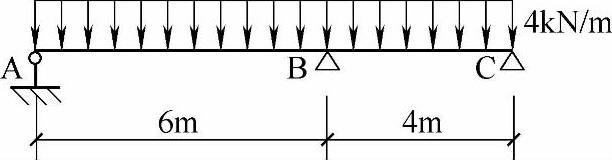
图 7.2.4
(式中γs为内力臂系数)(www.daowen.com)

【答案】 (B)
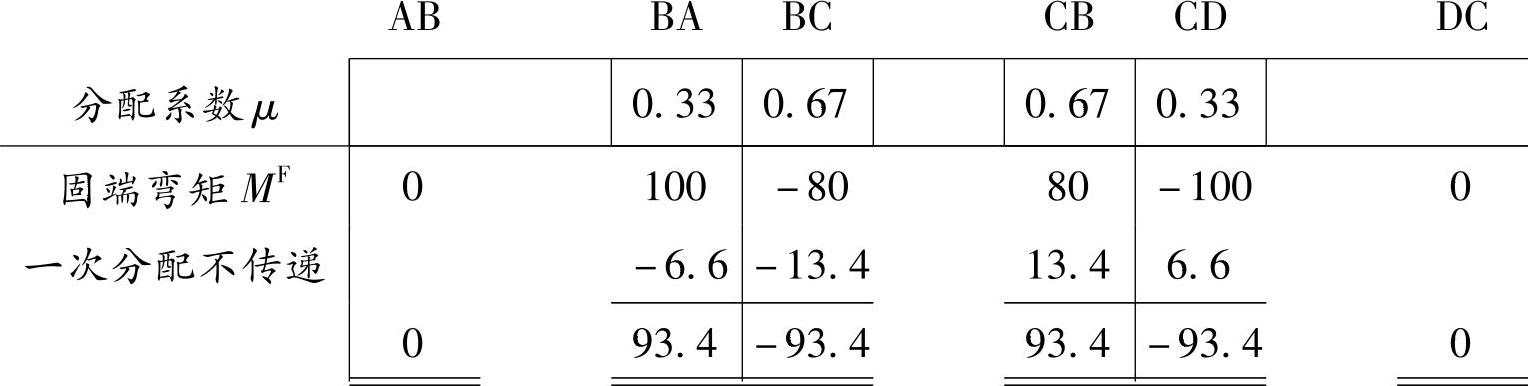
【解答】 选项的分子为支座B处的弯矩值,用力矩分配法求解:
因为超静定结构的内力只与杆件刚度的相对值有关,因此可以令EI=1。
固端弯矩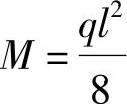 ,
,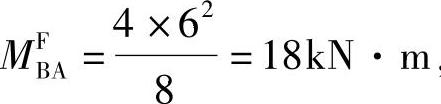 ,
,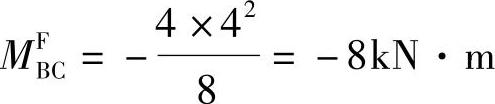

真题 【7.2.3】 (2002一级考题,原题为连锁题中的一道子题,现改写成一道独立题)
根据如图7.2.5所示的地沟计算简图及给出的B、C点的固端弯矩,并取1m长的地沟进行计算。假定侧壁固端弯矩MBA=-MCD=100kN·m(设计值)。底板固端弯矩-MBC=MCB=80kN·m(设计值),又已知侧壁和底板的弯矩分配系数μBA=μCD=0.33,μBC=μCB=0.67,试问一次弯矩分配后,MBC和MCB(绝对值)与下列何项数值相近?
(A)|MCB|=|MBC|=86.7kN·m
(B)|MCB|=|MBC|=93.4kN·m
(C)|MCB|=|MBC|=90kN·m
(D)|MCB|=|MBC|=66.6kN·m
【答案】 (B)
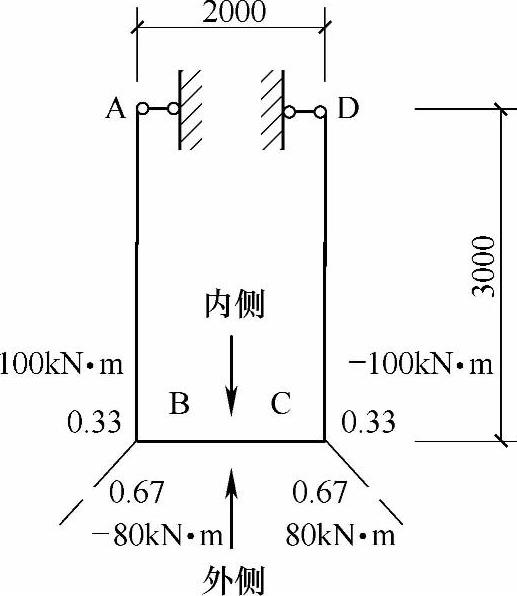
图 7.2.5
【解答】 一次分配,只需要计算一个杆端的分配力矩再加上固端弯矩即可
即MCB=MFCB+μCB[-(MFCB+MFCD)]=80+0.67×[-(80-100)]=93.4kN·m
【详解】
真题 【7.2.4】~【7.2.5】 (2001年考题,原题为一组大型连锁题中的两道子题,现经改写,已成一组小型连锁题)
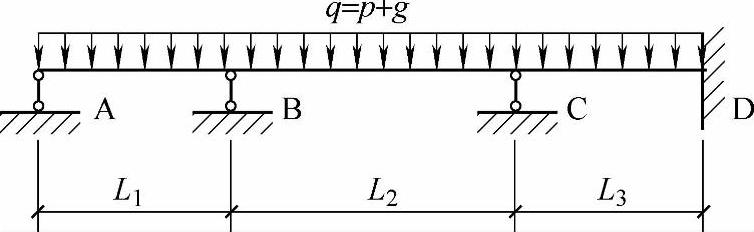
图 7.2.6
三跨钢筋混凝土等截面连续梁,q=p+g=30kN/m(设计值),如图7.2.6所示。梁截面b×h=200mm×550mm
真题 【7.2.4】 (2001年考题)
假定当L1=5m,L2=8m,L3=5m时,该梁弯矩分配系数μBA及B支座的不平衡弯矩ΔM应与下列何组数据相近?
(A)0.55,66.25kN·m (B)0.45,93.75kN·m
(C)0.385,253.75kN·m (D)0.625,253.75kN·m
【答案】 (A)
【解答】EI相等
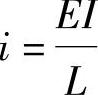 ,令EI=1,
,令EI=1,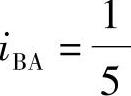 ,
,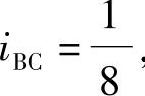
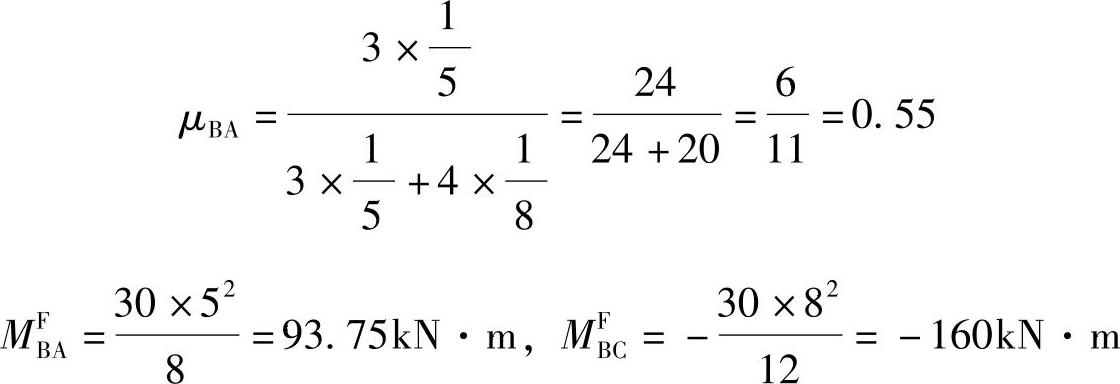
ΔM=93.75-160=-66.25kN·m
【详解】 等截面连续梁,EI相等
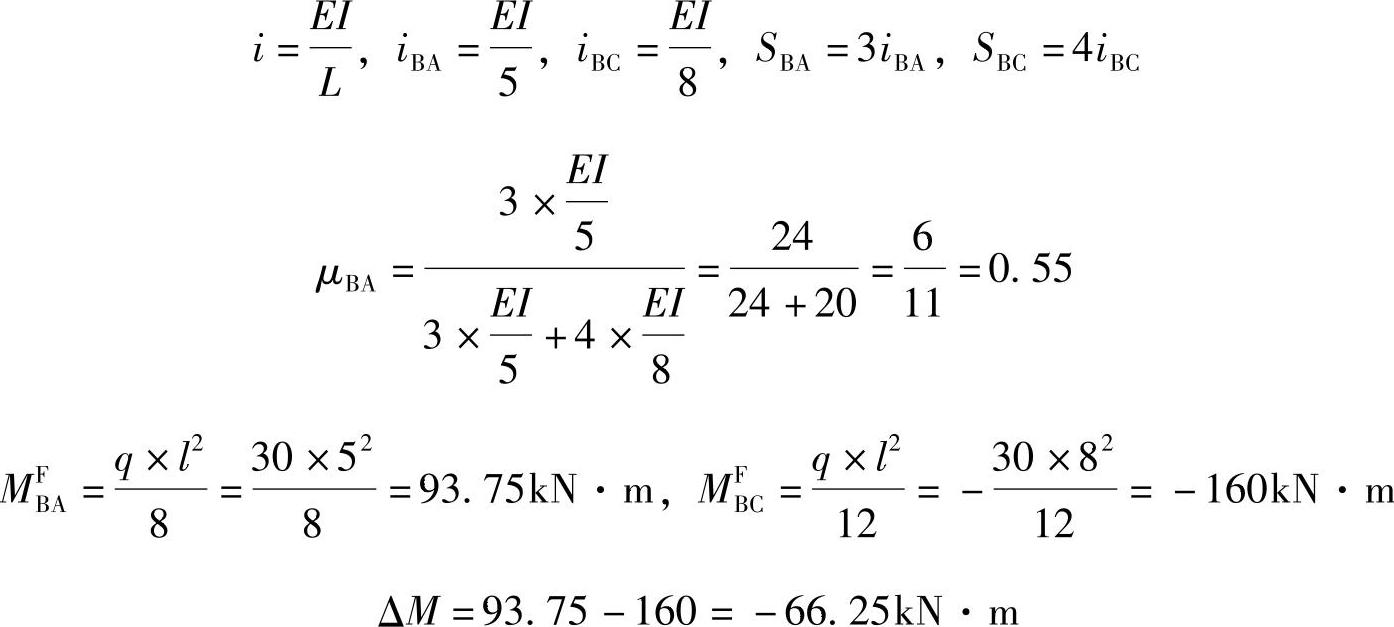
真题 【7.2.5】 (2001年考题)
假定调整L1,L2,L3跨度后的分配系数及各固端弯矩(设计值)如图7.2.7所示,试问该梁进行二次弯矩分配后,B、D支座的弯矩接近下列何组数据?
(A)MB=113.12kN·m,MD=129kN·m
(B)MB=153.12kN·m,MD=151kN·m
(C)MB=113.12kN·m,MD=140kN·m
(D)MB=153.12kN·m,MD=125kN·m
【答案】 (D)
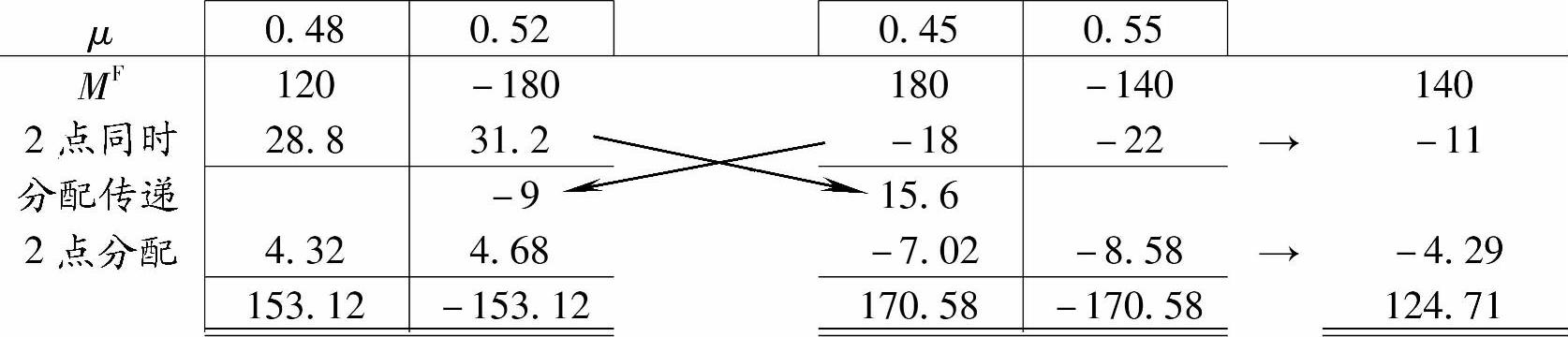
【解答】
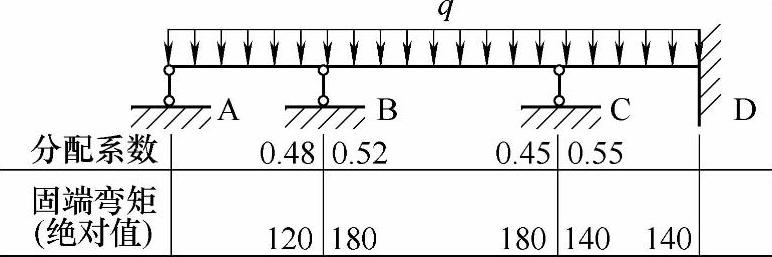
图 7.2.7
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







