设有如图7.2.1a所示的单节点刚架，其上各杆件均为等截面直杆。在一般忽略杆件轴向变形的情形下，该节点不发生线位移而只能有角位移。设在该节点1作用一集中力矩M，有三杆相交于点1。三杆的远端分别为铰接、固接和滑动支座。规定杆端弯矩与节点力矩（外力矩）均以顺时针为正，正号杆端弯矩反作用在节点隔离体，为逆时针方向。

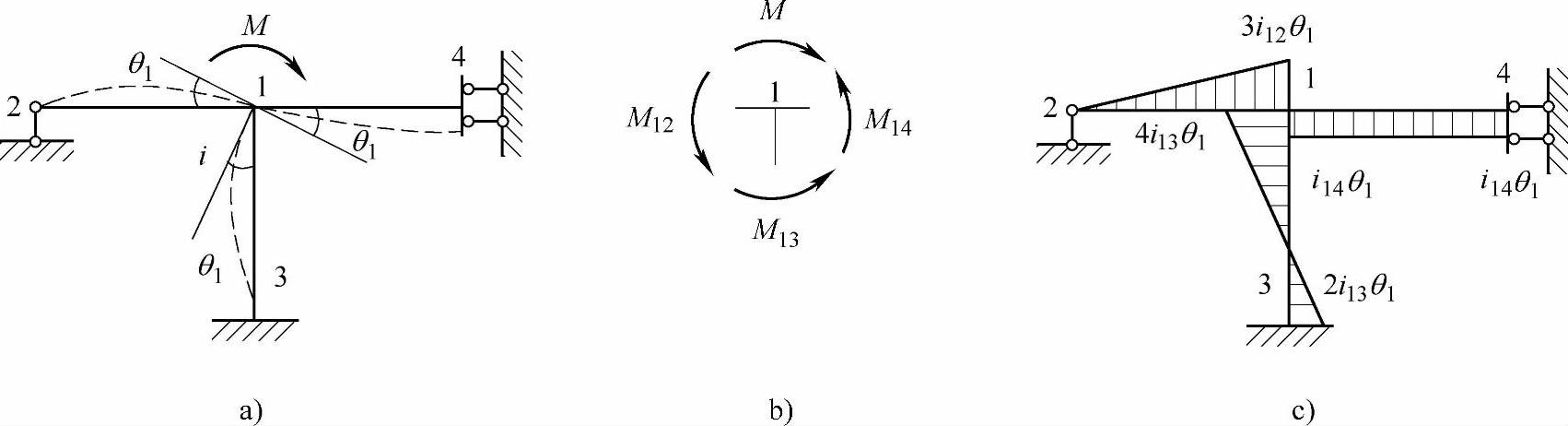
图 7.2.1

（一）转动刚度S

1.杆端的转动刚度S_1k

1k杆1端的转动刚度表示在1k杆的1端产生一单位转角时，在该杆端所需作用的弯矩。它反映了杆件杆端抵抗转动的能力。它的值取决于杆件的线刚度i和杆件另一端的支承情况。例如，12杆的远端是铰支端，S₁₂=3i；13杆的远端是固定端，S₁₃=4i；14杆的远端是定向支座，S₁₄=i。

2.节点的转动刚度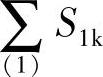

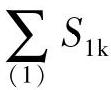表示汇交于节点1所有杆件在1端的转动刚度之和，称为节点转动刚度。其含义是使节点发生一单位转角θ=1所需的总力矩。

（二）分配系数μ

在M作用下，节点1产生转角位移θ₁。由上节所述的杆端转动刚度的定义可以写出各杆端弯矩（θ₁尚为未知）。

和节点1相交的各杆端弯矩，称近端弯矩，查表7.1.1知：

式（b）说明：汇交于刚节点1的各杆杆端弯矩之和等于刚节点上的外力矩M；或者说，刚节点1的外力矩M由汇交于该刚节点的各杆杆端“承担”。将式（a）代入式（b）。解得

将θ₁代回式（a）和式（b），即可求出各杆的杆端弯矩值如下：

近端弯矩

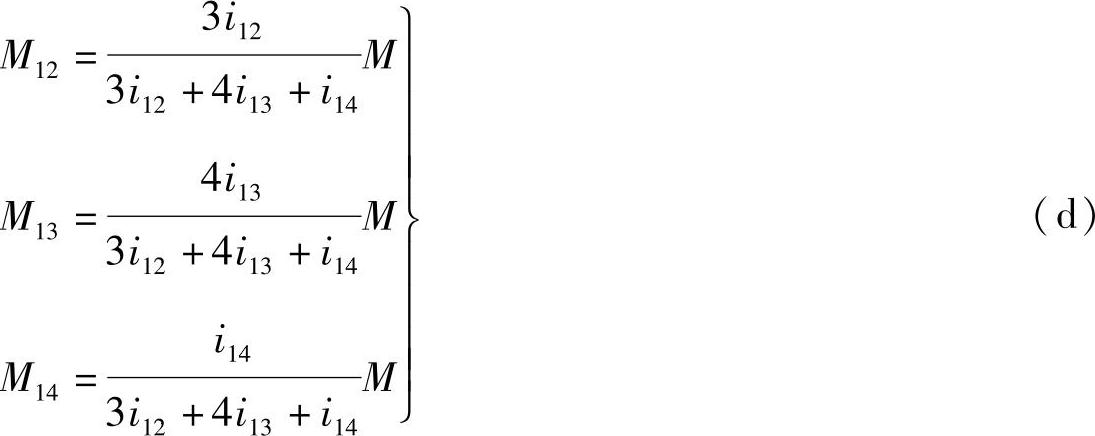
式（d）中的各杆近端弯矩可统一写成(www.daowen.com)

μ_1k称为力矩分配系数。是汇交于节点1的1k杆1端的分配系数，等于该杆1端的转动刚度S_1k与该节点的转动刚度∑S_1k之比值。而∑μ_1k=1，即汇交于同一节点各杆的分配系数之和应等于1，体现了节点的平衡条件。

（三）传递系数C

在M作用下，节点1产生转角位移θ₁后。

远离节点1的各杆另端的弯矩，称远端弯矩，查表7.1.1知：

M₂₁=0

M₃₁=2i₁₃θ₁

M₄₁=-i₁₄θ₁

将θ₁代入上式得远端弯矩

式（e）中的各杆远端弯矩可统一写成

M_k1=C_1kM_1k （f）

式中 C_1k——1k杆1端向k端的传递系数。

传递系数即表示当杆件近端（与节点相交端）发生转角时，远端（远离节点的杆件另一端）弯矩与近端弯矩的比值。对于不同的远端支承情况，相应的传递系数也不同。数值如下：

远端为固定支座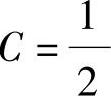

远端为滑动支座 C=-1

远端为铰支座 C=0