【摘要】:图7.1.9a、b所示为一组平行柱,各柱的一端为固定,另一端由刚性横梁连在一起,这种连接方式称为并联。显然,并联特点是各杆侧移相等。设在顶点作用有水平力P,则各柱剪力都等于P。图7.1.11b所示的柱B′D′与D′G′彼此串联,串联后可用图7.1.12所示的柱B″G″表示,其侧移刚度可按串联公式求得:。柱AF、B″G′按并联公式计算,刚架总侧移刚度为
图7.1.9a、b所示为一组平行柱,各柱的一端为固定,另一端由刚性横梁连在一起,这种连接方式称为并联。显然,并联特点是各杆侧移相等。并联各柱的总侧移刚度为各柱侧移刚度之和,d并=∑di
图7.1.10a、b所示为一组柱彼此串联的情况,各柱两端转角均设为零。设在顶点作用有水平力P,则各柱剪力都等于P。串联的特点是各杆受力相同,串联各柱的总侧移为各柱侧移之和(di为各杆侧移刚度)
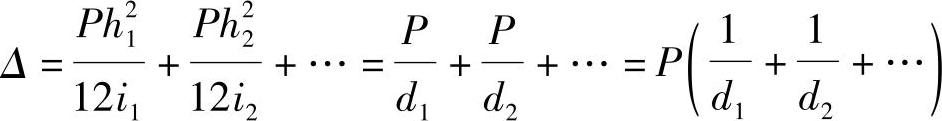
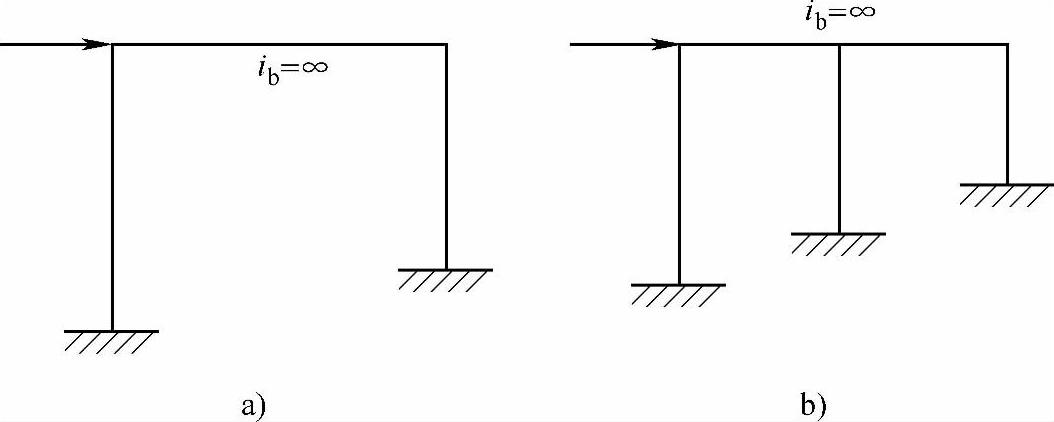
图 7.1.9
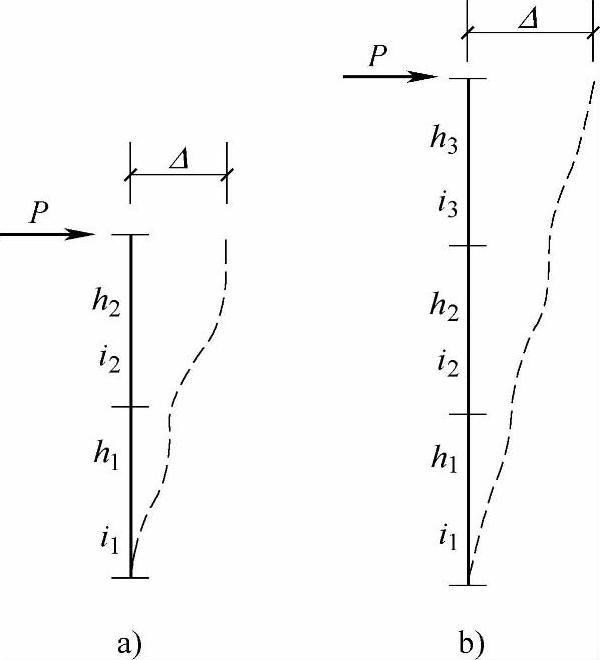
图 7.1.10
即 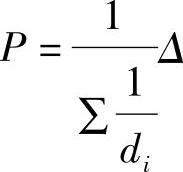
故串联各柱的总侧移刚度为
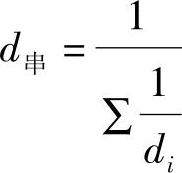
【7.1.1】 复式刚架的构件刚度
要求:计算如图7.1.11a所示复式刚架的总侧移刚度。图中柱侧所示为柱线刚度相对值。(https://www.daowen.com)
【解答】 图7.1.11a所示的柱BD与CE彼此并联,并联后可用图7.1.11b所示的柱B′D′表示,柱B′D′的侧移刚度等于柱BD与CE并联后的总刚度,即
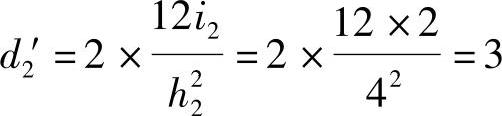
同样,图7.1.11a所示的柱DG与EH并联后可用图7.1.11b所示的柱D′G′表示,其侧移刚度为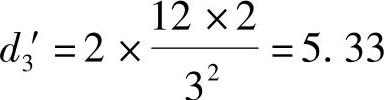 。
。
图7.1.11b所示的柱B′D′与D′G′彼此串联,串联后可用图7.1.12所示的柱B″G″表示,其侧移刚度可按串联公式求得: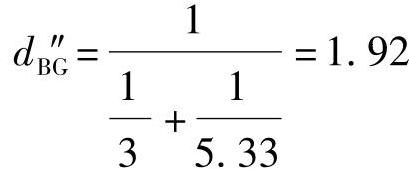 。
。
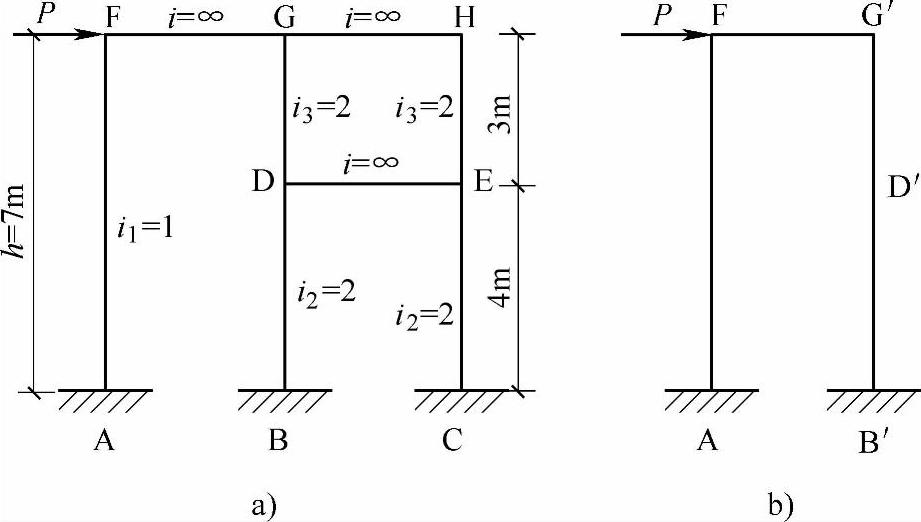
图 7.1.11
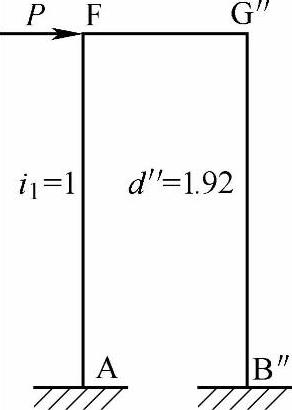
图 7.1.12
以上经过并联和串联,图7.1.11a所示的复式刚架已经转化为图7.1.12所示的等效简单刚架。柱AF、B″G′按并联公式计算,刚架总侧移刚度为
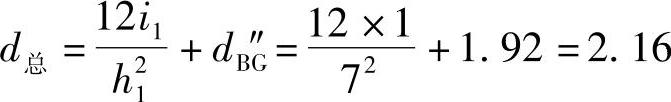
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






