在结构分析中，力和位移起着关键的作用。力和位移之间相互的关系是：力是位移的起因，位移表明力的存在，二者有着互为因果的关系。

例如，图7.1.1a所示的悬臂梁受到P力作用，在作用点处，沿着力的方向，梁产生了Δ的线位移。如果结构是线弹性体系，位移与荷载成正比增加，则荷载和位移之间的关系曲线是一条直线，如图7.1.1c所示，直线的斜率K作为刚度，得出其计算式为

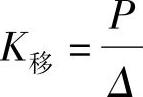
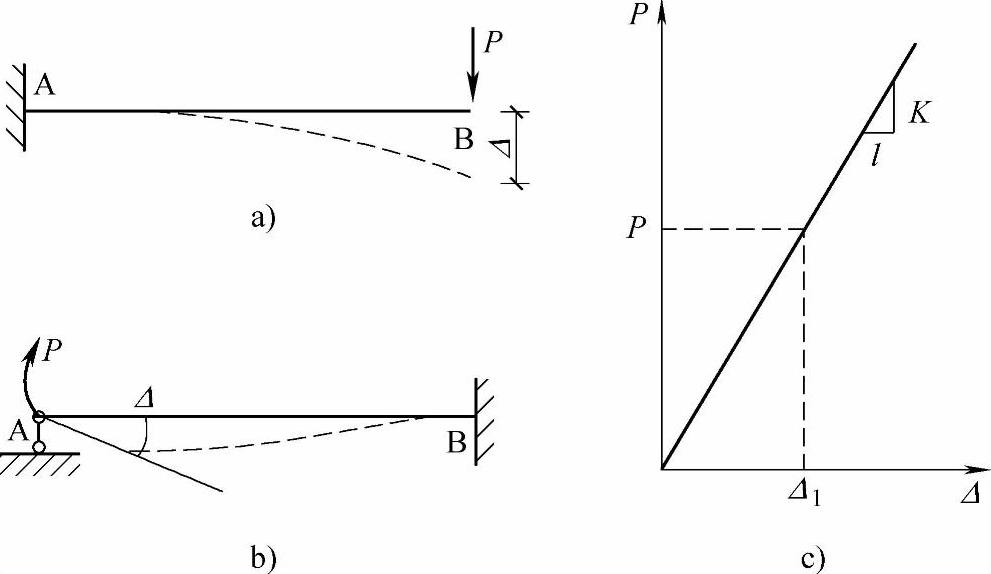
图 7.1.1

图7.1.1b所示单跨超静定梁，A截面在力矩P作用下转动了角位移Δ，位移曲线如图中虚线所示，则该梁A截面的转动刚度为

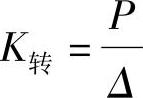
结构或构件刚度的一般表达式可写为

式中，P、Δ、K都是广义的，当P为力时，Δ即为沿力的方向产生的线位移，K即为沿该方向的移动刚度。当P为力偶时，Δ即为沿力矩方向的转动角度，K即为该方向的转动刚度。

式（7.1.1）既为结构或构件刚度的定义式，又是结构或构件刚度的计算式。它表明结构或构件对应某位移的刚度K，等于该处、该方向所作用的力与所产生的对应位移的比值。显然，在线弹性范围内，由于位移Δ与力P成正比，故刚度为常数。如图7.1.1c所示曲线的斜率即为刚度K。在非弹性范围内，刚度则为变量。(www.daowen.com)

刚度给出了与一组给定位移相联系的力的一种度量。对杆件结构来说刚度最基本的定义是杆件（结构）在力所作用的点产生单位变形位移时所需的作用力。反映的是杆件抵抗变形的能力。

工程上也常用到柔度δ的概念。柔度与刚度相反，定义为在单位力作用下杆件产生的变形（或位移），柔度与刚度互为倒数

一旦刚度被确定之后，则式（7.1.1）可写成下面的形式

P=KΔ （7.1.3）

式（7.1.3）说明，对刚度较大的物体使之产生相同位移需要使用较大的力。或者给出另一种表达形式为

式（7.1.4）说明，当外力一定时，物体的位移与它的刚度成反比。

刚度这个概念将贯穿结构分析的整个过程。无论是对结构进行定性分析，还是对结构进行精确的定量分析，都将经常用到刚度这个概念。下面就分别对结构设计中常用到的截面刚度、构件刚度、结构刚度等概念作些说明。