（1）静定结构反力、内力求解的基本方法是截面法：

1）用截面分开，取一部分为隔离体。

2）对隔离体进行受力分析，画出受力图。

3）根据受力图列平衡方程，求出未知力。

画隔离体受力图时，需注意所有约束都切断，以相应的约束力代替，即约束力要符合约束性质；所有受到的力要画全，包括内力、支座反力和荷载；已知力按实际方向画，未知力应按正方向假设，结果为代数值，其值的正负即为未知力的符号。

平衡方程三种基本形式：ΣX=0；ΣY=0；ΣM=0。

在平衡方程的建立和计算方面，要注意尽量避免解联立方程，最好使一个平衡方程只包含一个未知量，以方便计算，减少错误。

（2）静定单跨梁在工程中有着广泛的应用，常见的有简支梁、悬臂梁两种基本形式，以及伸臂梁（外伸梁）可以视为两种基本形式组合而成，如图6.1.1a、b、c所示。

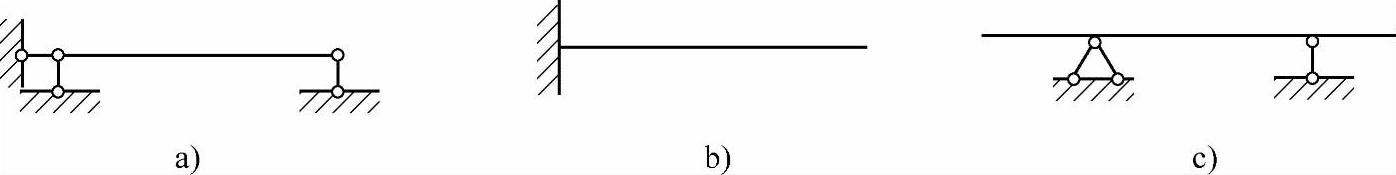
图 6.1.1

（3）平面结构杆件截面内力及符号规定，如图6.1.2所示。

1）轴力N，以拉为正。

2）剪力V，以绕杆端顺时针为正。

3）弯矩M，以下侧受拉为正（工程中的习惯，仅适用于梁）。

（4）作弯矩图和剪力图，如图6.1.3所示。

1）区段叠加法作弯矩图。确定区段两端弯矩后，叠加区段间相应简支梁的弯矩图。步骤是：

a）求控制截面的弯矩，即确定相应的控制点标距。

b）无荷载段：将控制点标距之间连接直线。

c）有荷载段：将控制点标距之间连接虚线，以虚线为基线叠加相应简支梁在荷载作用下的弯矩图。(www.daowen.com)

所得实线即为所求弯矩图，如图6.1.3b所示。

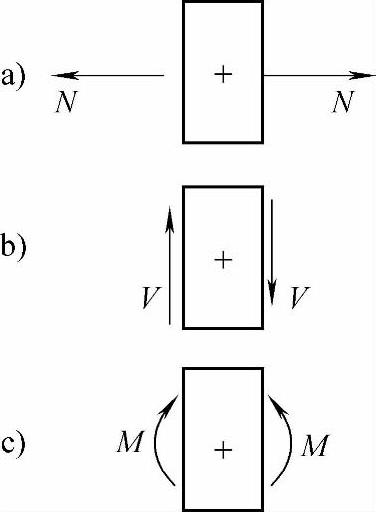
图 6.1.2

注意，叠加是指各截面弯矩值（弯矩坐标）的叠加，而不是弯矩图形的简单拼合。

2）滚小球作剪力图（口诀）。

力推小球同向走，力尽小球平行走，

反推小球回到零，上正下负剪力图。

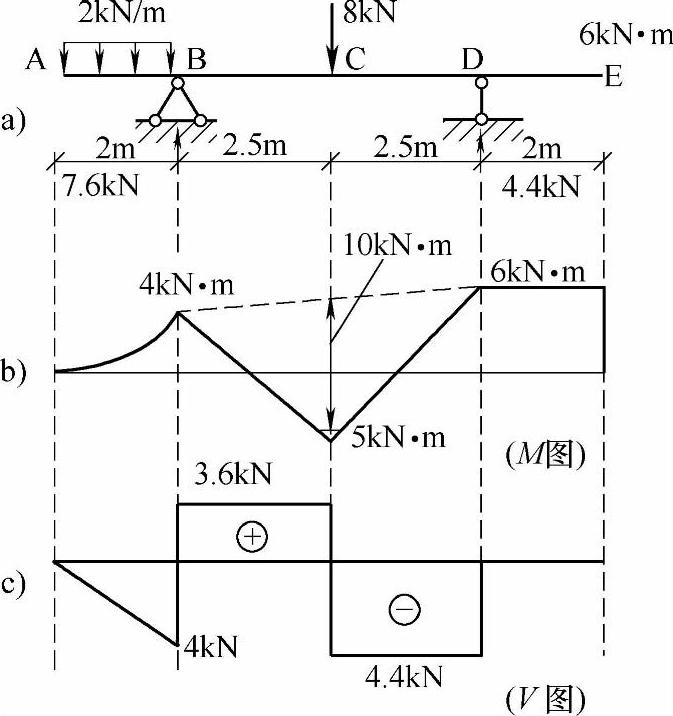
图 6.1.3

以图6.1.3为例说明上述做法。

弯矩图（可以不求反力），如图6.1.3a、b所示，两端外伸部分为悬臂梁，求出支座处弯矩M_B、M_D，虚线连接标距M_B、M_D，在此基线上叠加简支梁相应荷载的弯矩图，本例为中点叠加Pl/4=10kN·m。所得实线即为最后弯矩图。

具体如图6.1.3b所示（单位kN·m）：控制点为M_A=0、M_B=4、M_D=M_E=6；AB间为悬臂梁均布荷载弯矩图；DE间连接直线；BD间有荷载，连接虚线；在BD段中点，求出中点值为5，叠加简支梁受中点集中力的中点值Pl/4=10，得中点C的值为5（下侧受拉），连接B、C；C、D的竖标。则实线即为所求弯矩图。

剪力图，如图6.1.3a、c所示，（首先应求解反力，当所有外力均已知后）从左向右，只计竖向力，由杆端开始，按力大小滚动一段距离，然后平行滚动；遇到均布荷载则斜方向滚，均布荷载两端的差值即此段荷载的合力。其轨迹即为剪力图。最后一定回到零，这也是校核剪力图正确的标志。如果遇到集中力矩和中间铰均无影响。

如图6.1.3c所示，作剪力图（单位kN）具体的步骤：从左向右，连续画出的标距：从A（剪力等于零）开始遇到均布荷载则按均布荷载的合力确定两端的差值q×2=4得到C点标距为-4，连斜直线；力尽平行走，遇到Y_B，按力的方向，以力的值为长度从-4开始画标距7.6，得-4+7.6=3.6，力尽平行画，遇到C点集中力（竖向8），向下画到3.6-8=-4.4，力尽平行画，遇到Y_D=4.4向上画4.4到0，力尽应平行画，最后图形回到零（E点），得到剪力图正确。

（5）两种基本形式的简单荷载作用下的弯矩图和剪力图如图6.1.4所示。

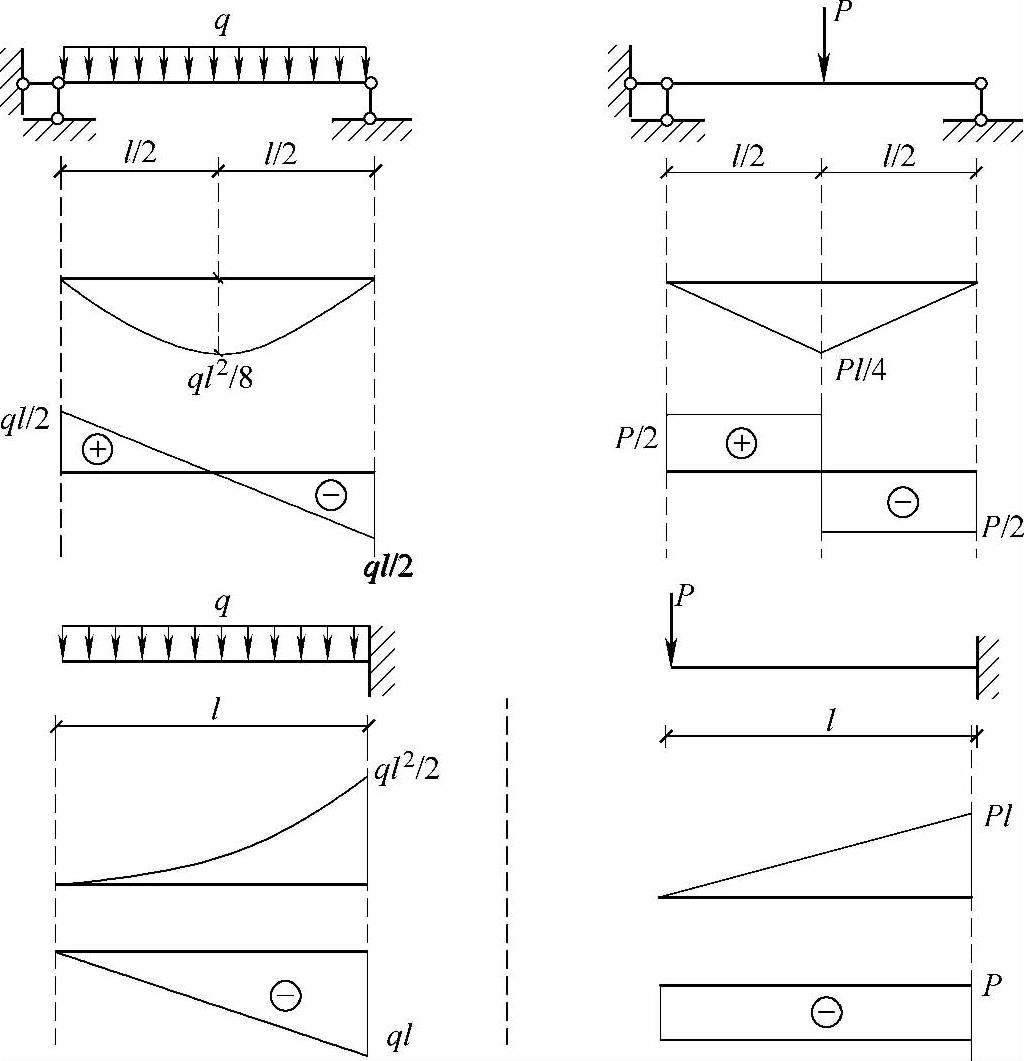
图 6.1.4