岩质边坡变形破坏的主要形式是滑坡与崩塌。边坡失稳常常是沿着顺层软弱结构面滑移。

边坡的稳定计算，主要是滑动破坏（即滑坡）的计算。目前有规范安全系数法、折线滑动法、毕肖普等圆弧滑动法、有限单元法等四大类。这些方法一般按照库伦定律或由此引申的准则进行。计算时，将滑体视为均质刚性体，不考虑滑体本身的变形，然后对边界条件加以简化以便于计算。如：将滑动面简化为平面、折面或弧面等，并将立体课题简化为平面课题，将均布力简化为集中力等来计算抗滑安全系数。但不论用哪种方法计算，都必须与工程地质分析结合起来，这样才能较正确地确定边界条件和计算参数，才能使计算成果具有实际意义。

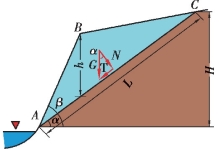
图5.17　边坡稳定计算剖面图

1）滑动面为一平面时的规范安全系数法

滑动面为一平面时，是最简单的情况，在由软弱面控制的顺层滑坡中常可见到。假定只考虑岩体自重，不考虑侧向切割面的摩擦阻力，垂直于滑动方向取一个单位宽度计算。沿滑动方向的剖面如图5.17所示。

抗滑稳定安全系数（K）可按下式计算：

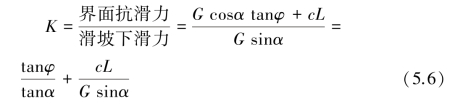
式中　Gsinα——滑坡下滑力；

　　　Gcosαtanφ+cL——界面抗滑力；

　　　L——斜坡滑动面长度；

　　　φ——界面内摩擦角；

　　　c——黏聚力。

假定滑体断面ABC为三角形，则滑体重力，代入式（5.7）简化后得：

式中　h——滑坡体高度；

　　　γ——岩石容重；

　　　K——安全系数，一般取1.2以上。

从式（5.7）可以看出，边坡的稳定安全系数是随着岩层滑动面倾角α角、滑体高度h的增加而降低，随着界面内摩擦角φ、黏聚力c值的增加而增大。

大多数边坡发生破坏时，均是在有水渗入岩体后发生。因此，计算时一般应考虑水压力的作用。此外，尚应考虑其他作用在斜坡上的动荷载以及地震力等。

2）滑动面为折线时的计算

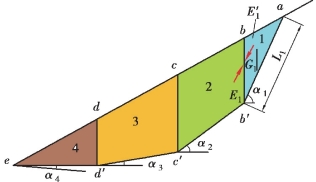
岩体中发生滑坡时，滑动面有时是由几组软弱结构面组成。此种情况下，取一沿滑动方向的剖面来看，其滑动面为一折线（见图5.18），此时可按推力计算法来计算其稳定性，即按折线的形状将滑坡体分成若干段，自上而下逐段计算，下滑力也逐段向下传递，算至末段即可判断其整体的稳定性。计算步骤如下：

取垂直于剖面方向为一个单位的宽度，按滑动面形状分为4段，每段的滑动面均为直线，并假定向上为正值。其他符号同前。

第一段滑体abb′的静力平衡计算（见图5.19a）：

式中　E1——第二段滑体bcc′b′对第一段滑体的推力，见图5.19（a），作用方向平行于ab′滑动面。

(www.daowen.com)

图5.18　滑动面为折线的滑坡剖面图

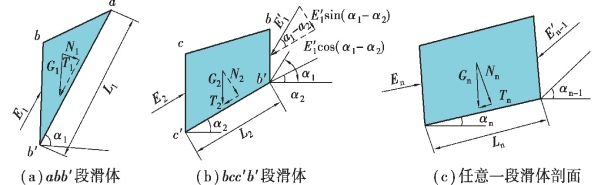
图5.19　滑体分段计算示意图

第二段滑体bcc′b′的静力平衡计算，见图5.19（b）：在计算第二段滑体时，除滑体bcc′b′本身重力产生的下滑力和抗滑力外，还有第一段滑体传递过来的推力E′1，它与上式中的E1大小相等方向相反，也可称为第一段的剩余下滑力，此外还有第三块滑体对第二块滑体的推力E2，它平行于滑动面b′c′，假定向上为正值（若计算结果为负值即为向下）。

式中　E2——第三块滑体对第二块滑体的推力。

同理，可列出任何一段（第i段）的平衡式（图5.31c）：

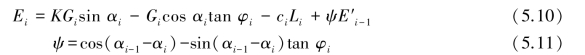
其中，

式中　ψ——力的传递系数；

其他参数同上。

按上述步骤依次计算至最后一段推力，m段的推力记作Em。若Em≤0，即m段没有推力，斜坡是稳定的；若Em>0，说明m段还有推力，所以斜坡是不稳定的。通过计算可知推力Ei在各段分布的情况，但在计算中，如果Ei出现负值时，表示滑坡推力不再向下一段传递，亦即滑坡岩体已经稳定，所以这时是安全的。

在实际工程中，可以通过先假定最后一段，代入式（5.11），求得再依次向前一段回推，最终求得安全系数K，若K>1（一般取1.2以上），滑坡体是安全的。

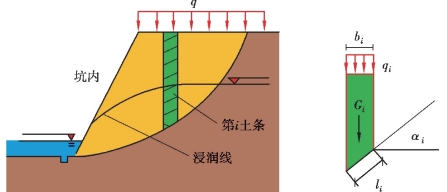
图5.20　圆弧滑动条分法计算简图

3）圆弧滑动条分法的计算

圆弧滑动面上的整体稳定性抗力分项系数可用条分法计算，如图5.20，按式（5.12）确定：

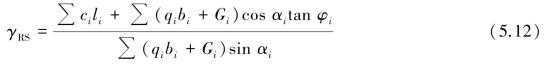
式中　γRS——整体稳定性抗力分项系数，γRS≥1.1～1.2；

　　　ci——第i土条滑动面上土的固结快剪抗剪强度指标标准值，kPa；

　　　φi——第i块土条的摩擦角，（°）；

　　　li——第i土条弧长，m；

　　　qi——第i土条顶面的地面均布荷载，kPa；

　　　bi——第i土条宽度，m；

　　　αi——第i土条弧线中点切线与水平线夹角，（°）；

　　　Gi——第i土条重量，kN/m。

在无渗流作用时，地下水位以上用土的天然重度（容重）计算，地下水位以下用土的有效重度计算；当有渗流作用时，对坑内外水位差之间的土，在计算滑动力矩时用饱和重度，计算抗滑力矩时用有效重度。