在任一典型图形中，总是有一条边的高差真值是已知的，解题时，首先是求其对边的真值，然后再求其余4个(伴随)观测值的真值，如果对边真值判断或计算有误，就将影响到后续的所有计算结果，因此这一步是极为重要而关键的，必须保证它的计算结果正确无误，下面将介绍利用误差距进行检验的一种方法。

在任一典型图形中，总是可以列出4个单环条件，条件的具体形式则与图形的结构有关。以图形D为例，它的4个单环条件为:

下面先推导ε1和ε6的“伴随误差距组合”的具体表达式。

将以上各式均乘以-0.5即可得到相应的再生真误差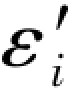(i＝2，4，3，5)，同时根据误差距的定义Δεi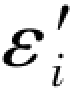＝-εi，则可写出以下各误差距表达式:

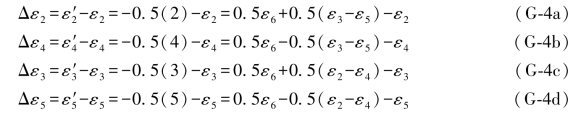
已知无1、6双环条件为(ε2-ε4)-(ε3-ε5)＝-10.2，若由上式分别求出Δε2-Δε3和Δε4-Δε5，即可得到ε1的两个伴随误差距组合，即

因此，在搜索对边6的过程中，这两个误差距组合的数值将始终保持10.4和-10.0不变，关键是(G-5b)式中ε6的两个“伴随误差距组合”，因为这两个组合中都含有搜索值的真误差，当搜索值越来越接近于真值时，其真误差ε6也就越来越小，直到等于零。

利用上式即可求得ε1的两个“伴随误差距组合”为:

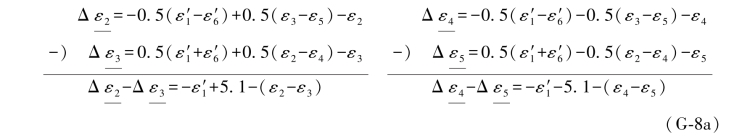
同样，可以求得ε6的两个“伴随误差距组合”为:

代入(G-8b)式，则有

则“辅助搜索值”为:

依次类推，很显然，“辅助搜索值”的真误差应为:

上式中ε6是代表原观测值L6＝58.9406的真误差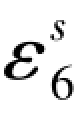，是各个搜索值的真误差，为避免混淆，将搜索值的真误差加了上标“s”(搜索)。例如，已经搜索到了58.9376，则利用该值替换一真向量(6-36a)式中的58.9406，于是有

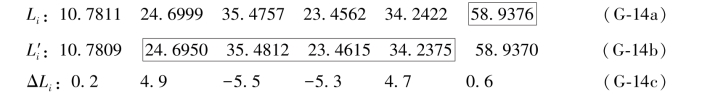
利用(G-14c)式中的误差距即可得到ε1的两个“伴随误差距组合”为:

又可以求得ε6的两个“伴随误差距组合”为:

以上相减结果均等于0.6，实际上它就是搜索值58.9376与再生观测值58.9370的差数，也就是它们所产生的误差距，往后将用符号(Δεi)1表示搜索值的误差距，(i＝1，2，…，6)，而用符号(Δεi)2表示辅助搜索值的误差距。(Δε6)1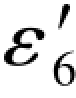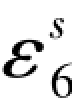＝-＝0.6这一数值在(G-14c)式就已经有了，这里之所以还要由(G-14a)式求出它的再生向量(G-14b)式，并求出误差距向量Δεi，主要是通过实得的数据验证前面理论推导过程和结果的正确性。搜索值58.9376的辅助搜索值是58.9391，为了进一步验证前面理论推导过程和结果的正确性，再次用58.9391替换(6-36a)式中的58.9406，于是有

利用(G-18c)式中的误差距可以求得ε1的两个“伴随误差距组合”为:

上述结果仍与(G-6)式中的结果相等。此外，又可得到ε6的两个“伴随误差距组合”为:

将(G-10a)与(G-10b)两式与以上两式对应相减得:

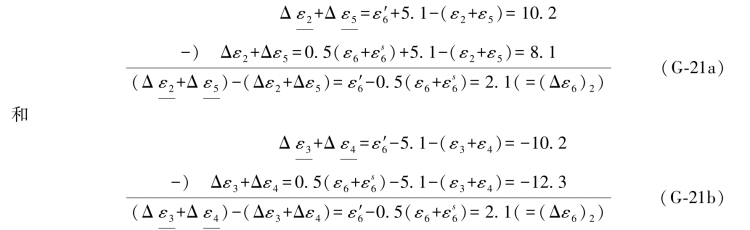
上述结果2.1实际上就是辅助搜索值与再生观测值的差数，也就是它们之间的误差距(Δε6)2，于是有

当某个搜索值正好等于真值时，则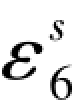等于零，于是由上式得到满足于真值时的公式:

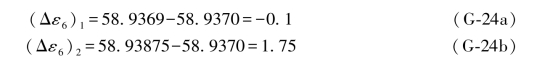
而且

当ε6等于零，则4个(伴随)综合误差公式应为:

相应地，4个误差距为:

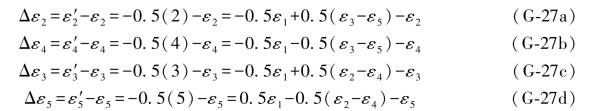
由此，可导出ε1的两个“伴随误差距组合”为:

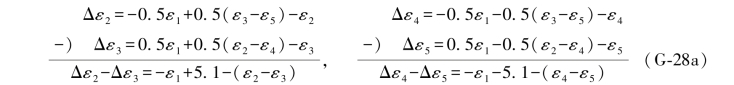
ε6的两个“伴随误差距组合”应为:

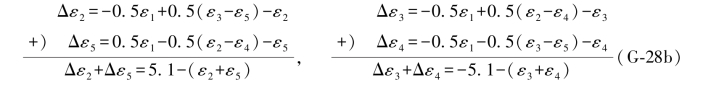
由(G-25)知，上式中ε2+ε5＝-5.2，ε3+ε4＝5.0，代入后得，

由上式中的误差距得:

以上(G-32a)和(G-32b)两式所得的结果，实际上就是搜索值10.7808与再生观测值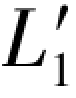＝10.7809所产生的负误差距-Δε1，如果用辅助搜索值10.78035，同样可以得到一个误差距。由于辅助搜索值的真误差应为:

式中，ε1是原观测值10.7799的真误差，εs1则是搜索值的真误差，它是不断改变的。由辅助搜索值所得到的误差距应为:

(G-33a)式是L1辅助搜索值的真误差，而(G-33c)式则是其辅助搜索值的误差距，它是由一固定的常数与搜索值误差距两式合成，故可写出L1搜索值的误差距和其辅助搜索值的误差距分别为:

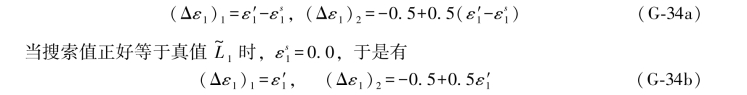
例如，当搜索值为10.7811时，它的辅助搜索值为10.7805，于是有

前面已经详细地介绍了有关理论，这里将只作必要的解释，并直接写出相关公式。

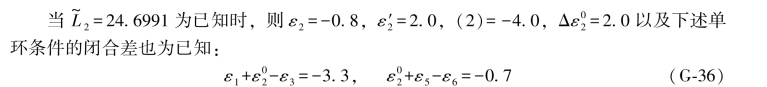
根据表6.7　即可写出ε2＝0.0时的4个(伴随)综合误差公式为:

根据Δεi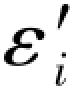＝-εi＝-0.5(i)-εi(i＝1，6，3，5)，即可写出4个(伴随)误差距表达式为:

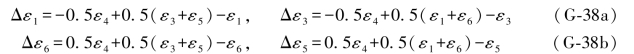
已知无2、4双环条件为(ε1+ε6)-(ε3+ε5)＝-2.6，于是可以得到ε2的“两个伴随误差距组合”为:

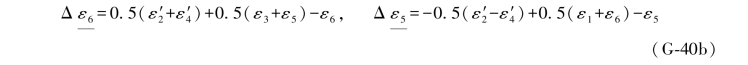
由上式即可写出ε2的两个“伴随误差距组合”为:

同样，可以写出ε4的两个“伴随误差距组合”为:

在(3-45c)式中就已经给出(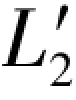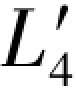，)混合向量的误差距，于是由(G-41a)和(G-41b)两式即可写出以下各式:

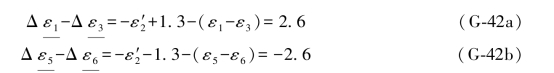
以及

由上述误差距可以求得ε2的两个“伴随误差距组合”为:

上述结果与(G-39c)式给出的结果完全相等，表明前面推导过程和结果的正确性，此外，又可求得ε4的两个组合为:

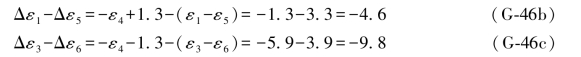
在以上两个结果中都包含有搜索值23.4564的真误差ε4。将以上两式分别与(G-43a)式和(G-43b)式对应相减得:

例如，当搜索到23.4567时，它的辅助搜索值为23.45645，于是有:

此时，4个(伴随)综合误差(i)(i＝1，6，3，5)公式中的ε4等于零，于是有:

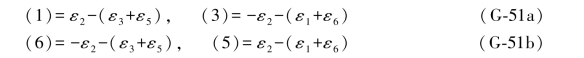
按照前面所讲的同样方法，即可得到它们的误差距表达式为:

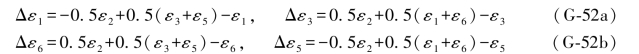
利用上式即可得到ε2的两个“伴随误差距组合”为:

又可得到ε4的两个“伴随误差距组合”为:

此时，在ε2的两个误差距组合中包含有L2搜索值的真误差ε2，它是随着搜索值的改变而改变，而由(G-50)式知，在ε4的两个误差距组合中，(ε1-ε3)＝5.6，(ε3-ε6)＝8.2，故有

由(G-55c)式中的误差距得出ε4的两个误差距组合为:

上述结果与(G-53c)式中的结果完全相等，而ε2的两个组合则应为:

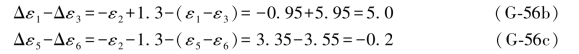
将(G-42a)和(G-42b)两式分别与以上两式对应相减得:

式中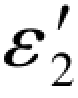，(-ε2)实际上就是L2的原观测值24.6999与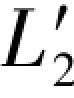所产生的误差距，它的数值在表1.1中就已给出，即Δε2＝2.8，因此上式也可写成:

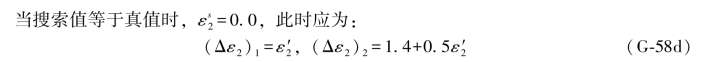
例如，当搜索到24.6991时，它的辅助搜索值为24.6995，于是有:

4个(伴随)误差距为:

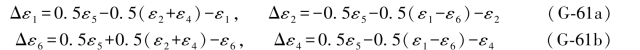
已知无3、5双环条件为(ε1-ε6)+(ε2+ε4)＝4.6，由此即可写出ε3的两个“伴随误差距组合”为:

ε5的两个“伴随误差距组合”为:

顾及(G-60)式，则有

由(G-64c)式中的误差距得:

上述结果与(G-62c)式中所给出的结果完全相等。

此外，还可导出与(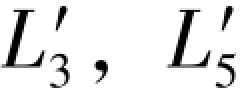)混合向量的4个误差距表达式为:

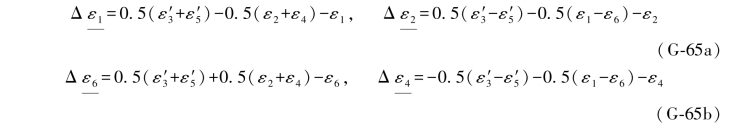
由此即可分别得到ε3与ε5的两个误差距组合，同时顾及(3-52c)式中的误差距数值，即可得到以下结果:

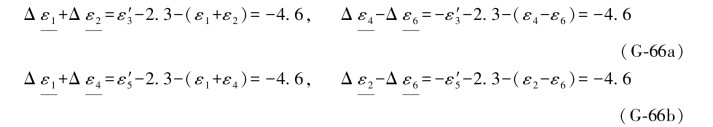
将(G-64c)式中的误差距代入(G-62b)式，即可得到ε5的两个误差距组合为:

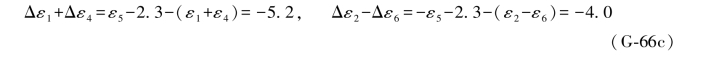
将(G-66b)式与(G-66c)式中的两式对应相减，即可得到

式中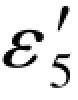，(-ε5)实际上就是L5最初始的误差距，由表1.1知Δε5＝3.8，因此上式也可写成:

此时4个(伴随)误差距表达式应为:

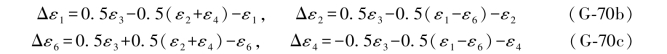
于是可以写出ε3的两个误差距组合为:

以及ε5的两个误差距组合为:

顾及(G-70a)式，上式中的(ε1+ε4)＝1.7，(ε2-ε6)＝2.9，故有

假设在对L3进行搜索时，采用了下述一系列搜索值以及相应的辅助搜索值:

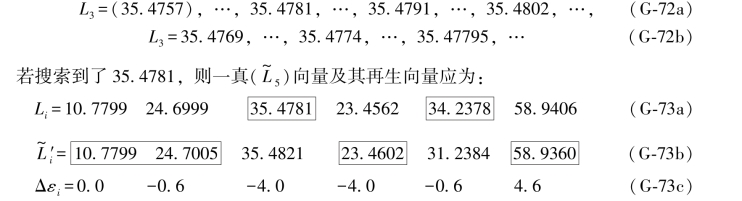
由(G-73c)式中误差距可求得:

将上述结果与(G-71c)式比较知，两者完全相等，而(G-71a)式应为:

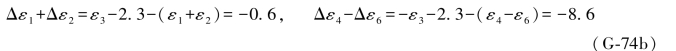
显然上式中的ε3是搜索值35.4781的真误差，将(G-66a)中的两式与(G-74b)中的两式对应相减得:

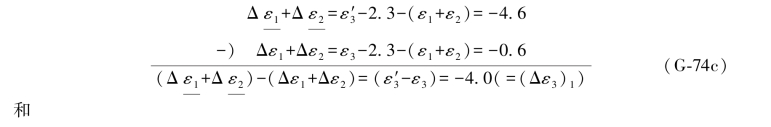
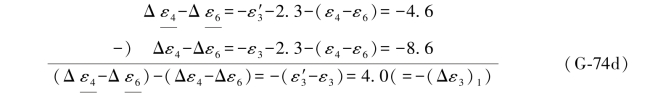
以上两式求得的都是搜索值35.4781的误差距，即

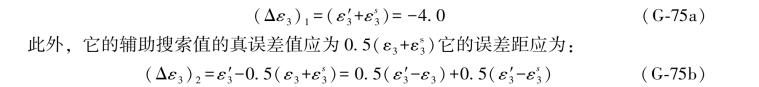
上式中(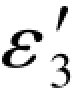-ε3)实际上就是L3原观测值的误差距，在表1.1中就已给出，即Δε3＝-6.4，因此，上式也可写成:

(Δε3)2的具体数值可按下式求得:

如果将(G-75a)式中的(Δε3)1＝-4.0代入(G-76a)式中，则有

而且由(G-76a)式可求得:

(G-78b)与(G-78c)两式求得的结果相等，故35.4802应为真值。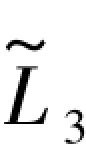

4.在求对边真值时，利用误差距进行检验的理论分析

前面讨论了图形D三组互为对边在求对边真值时利用误差距组合进行检验的具体方法，以下内容将具体分析它的理论依据。

对于图形D而言，最初始的误差距向量为(表1.1):

由此得出ε1的“伴随误差距组合”为(为了简便起见，以下均简称为“误差距组合”):

根据前面(1)中的推导方法，即可得到以下结果:

ε1的误差距组合为:

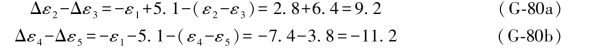
ε6的误差距组合为:

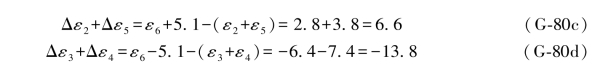
同样，参照(2)中的推导，即可得到以下结果:

ε2的误差距组合为:

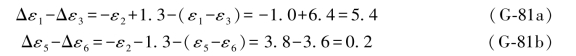
ε4的误差距组合为:

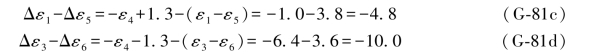
又参照(3)中的推导，即可得到下述结果:

ε3的误差距组合为:

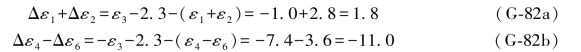
ε5的误差距组合为:

由上述举例可以看出，求解的实质也就是通过搜索找到对边误差距组合的应有数值。对于图形D而言，也就是由(G-79)、(G-80)、(G-81)诸式中最初始的误差距组合的数值改变成双真向量情况下所应有的数值，即

此外，由(G-6b)式和(G-28c)式知，还可以满足以下条件:

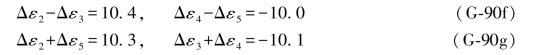
若满足(G-48d)或(G-58d)两式中的条件，则一定同时满足以下各条件:

以及

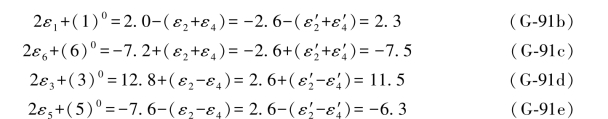
此外，由(G-46a)式和(G-56a)式知，还可以满足以下条件:

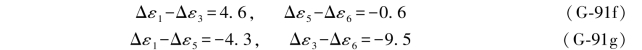
若满足(G-68c)或(G-77)两式中的条件，则一定同时满足以下各条件:

以及

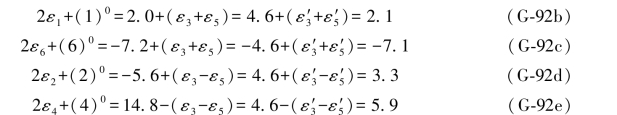
此外，由(G-62c)式和(G-71c)式知，还可以满足以下条件:

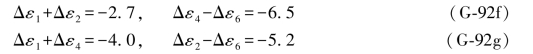
满足了上述条件之后，还可以应用附录F中给出的各种方法予以确认和复核。

5.关于搜索对边真值问题的进一步研究与讨论

在本书前面部分已经定义“真值”就是其真误差等于零的观测值，但是还可以从另一个角度来理解“真值”的含义。对任何一个“量”(例如，距离、角度、高差，等等)进行观测所产生的“真误差”都是相对于该“量”的“真值”而言的。“真值”是客观存在的，任何一个“量”，既不可能没有它的“真值”，也不可能同时存在两个或两个以上的“真值”。在进行观测之前，是无法预计会产生什么样的“真误差”，其数值是大还是小，是正还是负。但是一旦观测完成之后，它相对于该“量”所产生的“真值差”就已经是一个确定不变的具体数值了。以图形D为例，相对于6个(模拟的)高差真值而言，其“真误差”分别是(见表1.1):

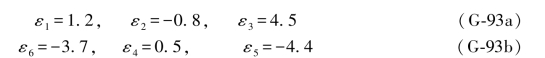
对于水准网而言，必须要有1个高精度测定的高差作为起算高差，因此，在“求真法”中认为在每个典型图形中一定有1边的高差真值是已知的，该真值可能是经过高精度直接测定的，大多数则是由其相邻图形传递过来的。

在图形D中有了6个高差观测值之后，就可以列出不同形式的条件方程。例如可以列出4个单环条件为:

还可以列出3个双环条件，即

但是在1个典型图形中，只有1个高差真值是已知的，其余都是未知的。在此情况下，如何保证准确无误地求出所有的真值，这正是本书前面所有理论阐述和导出的公式所要达到的目的。从以上讨论可以看出:首先，任何1个“量”，不但真值是客观存在的，而且是唯一存在的。其次，所谓“真值”既可以理解为“真误差等于零的观测值”，也可以理解为“它对其余真误差不产生任何干扰的数值”。

由于真值和真误差都是未知的，只能通过搜索找出，而如何保证搜索不会发生误判，这正是“求真法”中1个极其重要而关键的问题。

②双环条件的“统一符号表达式”。

在搜索真值时，采用双环条件比单环条件更为简便有利。在1个典型图形中，随着已知边所在位置的不同，总是可以归纳成3种情况，即以ε1、ε6，ε2、ε4，或ε3、ε5为主的3种情况。对于图形D而言，这3种情况已经在表6.4中给出。其中第1组的头两个条件是以(ε1+ε6)和(ε1-ε6)为主项的条件，它的副项分别为-(ε3+ε5)和(ε2+ε4)，第3个条件则是无1、6的条件，因其中不包含ε1和ε6，所以在搜索过程中，它的闭合差始终为-10.2。在以(ε2+ε4)和(ε2-ε4)为主项的第2组中，它的副项分别是(ε1-ε6)和-(ε3-ε5)，而第3个条件则是与ε2、ε4无关的条件，因此它的闭合差始终等于-2.6。类似地，在以(ε3+ε5)和(ε3-ε5)为主项的第3组中，它的副项分别是-(ε1+ε6)和-(ε2-ε4)，其中第3个条件与ε3、ε5无关，因此，它的闭合差等于4.6不变。为了讨论和书写简便起见，现在就用下述统一的符号来表达，即

于是表6.4中所列的3种情况就可写成如下形式:

第1组:

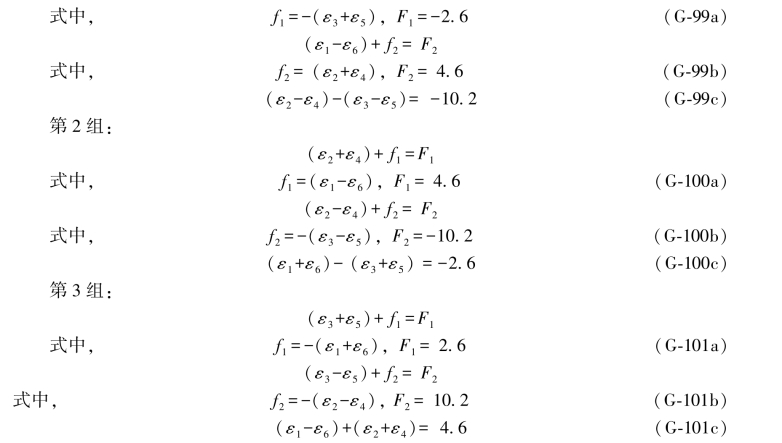
对于第1组而言，将(G-98a)和(G-98b)两式相加并相减，即可分别得到第1、6两个双差和方程，即

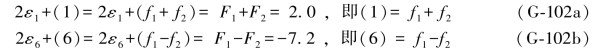
对于第2组而言，由(G-100a)和(G-100b)两式相加并相减，即可得到第2、4两个双差和方程，即

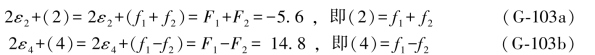
同样对于第3组，由(G-101a)和(G-101b)两式相加并相减，即可得到第3、5两个双差和方程，即

在实际工作中，随着已知边所在位置的不同，只可能涉及上述3种情况中的一种，采用统一符号的优点是，不仅书写方便，而且具有明显的规律，即两个副项之和(f1+f2)是主边(指1、2、3三边)的综合误差(1)、(2)、(3)，而两个副项之差(f1-f2)则是其对边(指6、4、5三边)的综合误差(6)、(4)、(5)。在两个副项中，只包含4个(伴随)观测值的真误差，所以在搜索过程中，它们的数值保持不变，因此每一组中的副项都是不变的常数。此外，两个闭合差之和(F1+F2)是3个主边双差和方程的常数项，两个闭合差之差(F1-F2)则是3个对边双差和方程的常数项。闭合差F1和F2是随着搜索值而改变的，所以双差和方程的常数项是在不断改变的。由于上述原因，采用了统一的符号，就可以看到了什么符号，就知道它代表了什么数值。

③从再生真误差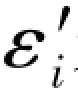来理解“解的存在”和“解的唯一性”。

在前面的①中通过图形D的模拟数据阐述了如何理解“真值”的含义，而“真值”既可以理解为其真误差等于零的观测值，也可以理解为它对其余真误差不会引起任何干扰的数值。现在再通过再生真误差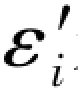来理解“解的存在”和“解的唯一性”。

由以上两式可以写出:

由以上两式可以写出以下两式:

由以上两式即可写出如下两式:

由此可以得到以下两式:

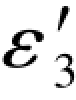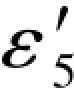两个副项(ε1+ε6)和(ε2-ε4)中的真误差是4个(伴随)观测值的真误差，只要这4个观测值未变，则两个副项都是确定不变的常数。因此，和不仅是存在的，而且是唯一的，不可能有另一种解答。

以上通过再生真误差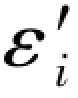进一步说明了，任何1个典型图形都是有解的，而且是唯一的。实际上，以上导出的结果就是图形的等值关系式，在表7.4中就已经列出了图形D的等值关系式。不同的图形都有一套不同的等值关系式。

④F1、F2几种函数式的推导。

由该向量列出的双环条件应为:

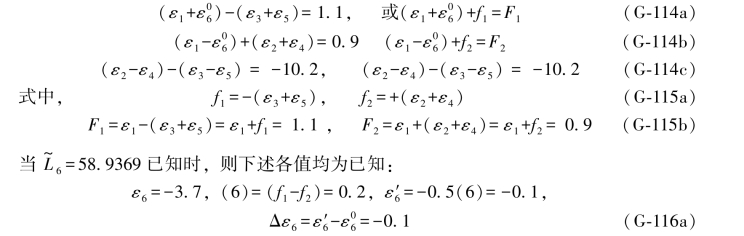
于是有

由(G-117a)式可以列出6个双差和方程为:

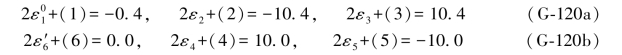
根据(G-119a)式中的真误差，并对照表6.7中图形D的综合误差公式，即可写出以下各式:

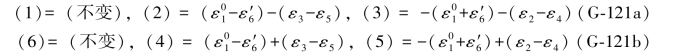
于是(G-120)式可以写成如下形式:

还有第3个条件没有写出。由(G-118a)式可以列出6个双差和方程为:

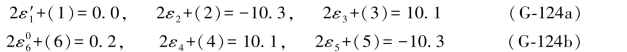
同样，根据(G-123a)式中的真误差向量，并对照表6.7中的综合误差公式，即可写出下述双差和方程的综合误差表达式如下:

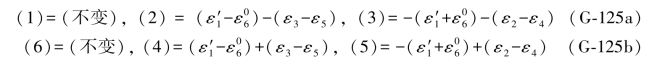
于是(G-124)各式可以写成下述形式:

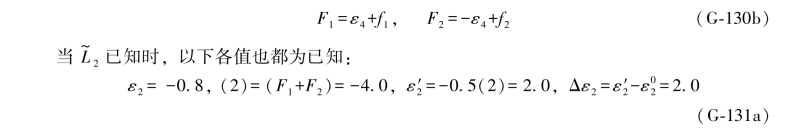
于是有

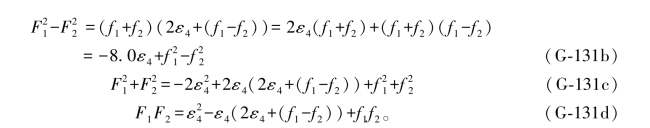
式中，(2ε4+(f1-f2))＝2ε4+(4)，实际上就是第4双差和方程。

由此列出的双环条件为:(www.daowen.com)

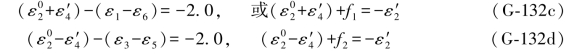
第3个条件未写出。由(G-132a)式可列出6个双差和方程为:

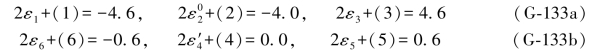
根据(G-132b)式对照表6.7中综合误差公式即可写出下式:

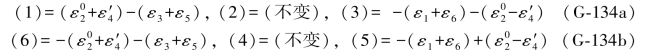
于是(G-133)式即可写成如下形式:

其真误差向量应为:

由该向量列出的双环条件为:

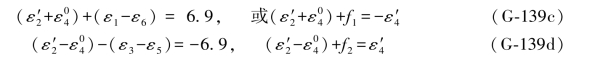
由(G-139a)式可列出6个双差和方程为:

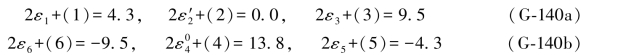
顾及(G-138b)式，即可写出各综合误差式如下:

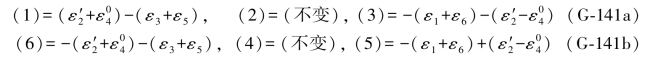
于是(G-139)各式可写成以下表达式:

于是可以写出以下各式:

它的真误差向量应为:

由其列出的双环条件为:

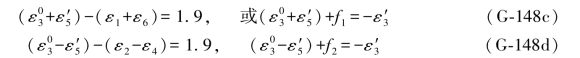
第3个条件未写出。由(G-148a)式可列出6个双差和方程为:

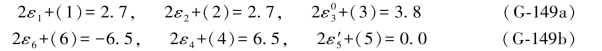
根据(G-148b)式并对照表6.7中的公式，即可写出各综合误差表达式:

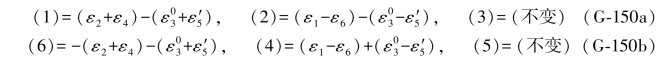
于是可以写出(G-149)式中各双差和方程的具体形式为:

于是可以写出以下各式:

其真误差向量应为:

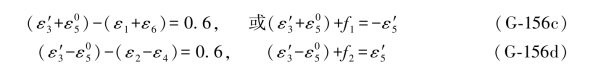
并可列出6个双差和方程为:

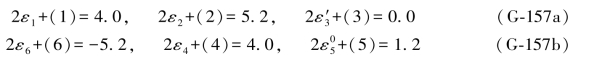
顾及(G-156b)式即可写出上式中各综合误差的表达式为:

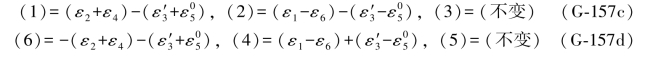
于是有:

(G-167a)式中的左右两式就是(G-119b)和(G-119c)式。(G-167b)式中的左右两式就是由(G-117b)式列出的再生条件。由(G-117b)减去(G-117a)式，即得(G-167c)式中的误差距条件。

有关(G-167)各式数值之间的关系和规律，在6.4节中已经作了初步的阐述，可以参阅，这里不再重复。这里特别提醒的是，第1和第4数值点上的数值总是数值相等正负相反，而第2和第3数值点上的数值也是一样，数值相等正负相反。因此，在(G-167b)左边的公式中，其中-(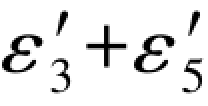)一定与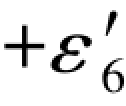数值相等正负相反，而在右边公式中，其中+(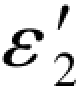+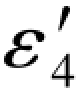)一定是与-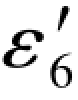数值相等正负相反。于是(G-167)各式即可改写成如下形式:

根据以上闭合差即可计算出F1、F2的各种函数值，结果列在附表2中。

附表2　图形D 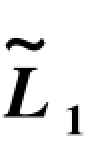已知时F2的不同函数值

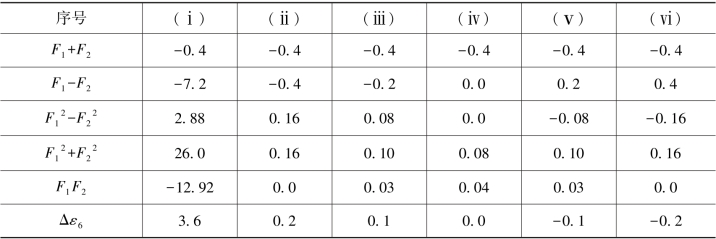
为了便于实际应用，再将(G-113c)、(G-113e)三式作进一步的简化。由(G-127b)、(G-127c)、(G-127d)式知:

将以上各式分别代入(G-113c)、(G-113d)、(G-113e)三式，则有

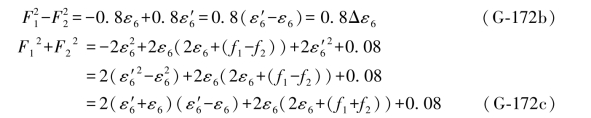
考虑到上式中的第6双差和方程应等于其误差距Δε6的-2倍(2-27式)，于是上式应为

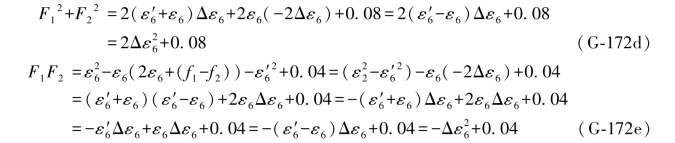
为了应用方便起见，现将上述结果以及(G-127)各式一并抄录于下:

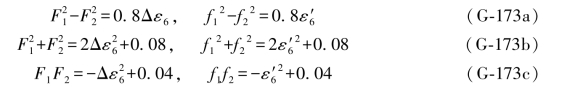
从以上公式可以看出，条件闭合差F1、F2的函数值只与对边6的误差距Δε6有关，它是随搜索值不断改变。而副项f1、f2的函数值只与对边6的再生真误差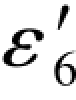有关，f1、f2都是确定的常数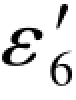，是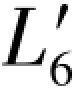＝58.9370的真误差，它也是确定的数值。因此，求其对边6的真误差或真值，关键也就在于如何正确解出。

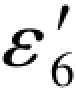根据上述闭合差F1、F2即可算出附表3中的数值。

附表3　图形D 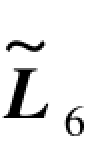已知时F1、F2的不同函数值

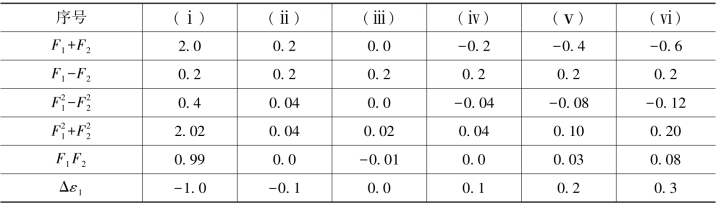
为了方便起见，也和前面一样，须将(G-116c)、(G-116d)、(G-116e)各式利用(G-128b)、(G-128c)、(G-128d)予以简化。由于其方法和前面的(G-118)各式完全相同，为了节省篇幅不再作具体推导，只将结果写在下面，即

为了后面查阅方便起见，现将有关2边、4边以及3边、5边的公式集中写在下面。

分别由(G-138b)、(G-138c)、(G-138d)式以及由(G-131b)、(G-131c)、(G-131d)式化简并分别由(G-144b)、(G-144c)、(G-144d)以及由(G-143b)、(G-143c)、(G-143d)式，即可得到以下两组公式:

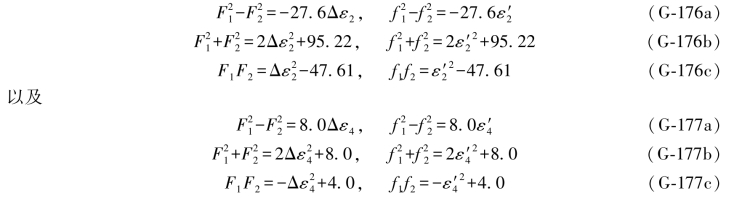
同样地，分别由(G-155b)、(G-155c)、(G-155d)以及由(G-147b)、(G-147c)、(G-147d)式化简，并分别由(G-160a)、(G-160b)、(G-160c)以及由(G-152a)、(G-152b)、(G-152c)式，即可得到以下两组公式:

6.求对边真值时的数值规律及其具体算法

在上节(5)中，为了便于书写与简单明了，对双环条件的副项采用了统一的符号，并进而导出了不同情况下用于检核的公式。下面将说明寻找对边真值时所呈现出的数值规律，从而提出判定真值的条件。

仍然先以图形D的1边和6边为例。假设已知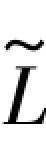1＝10.7811，则以下各值均为已知，即

为了能够利用已知的误差距，故除了列出上述条件之外，还须由表3.1中的再生向量列出相应的再生双环条件。为了能够利用误差距条件，要将有关条件按下述方式分成两组:

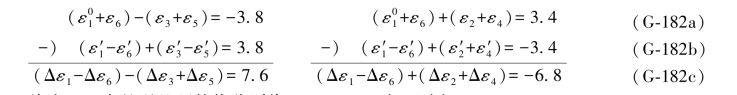
将表3.1中的误差距数值分别代入(G-182c)式，则有

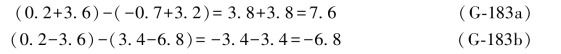
由上述结果可以看出，每个误差距条件中的两项总是数值相等的，且等于闭合差的二分之一。这一性质在搜索过程中也不会改变。为了叙述简便起见，以后就简称这种性质为“两项相等性质”。例如，在(G-183a)式中，(Δε1-Δε6)＝-(Δε3+Δε5)＝3.8，在(G-183b)式中，(Δε1-Δε6)＝(Δε2+Δε4)＝-3.4。此外，要提出的是，(G-182c)式中的误差距条件是由(G-182b)式减去(G-182a)式而得，而不是相反。

根据表3.1中的数据，可以算出以下各值:

将以上数据分别代入(G-182a)和(G-182b)的两组条件中，则有

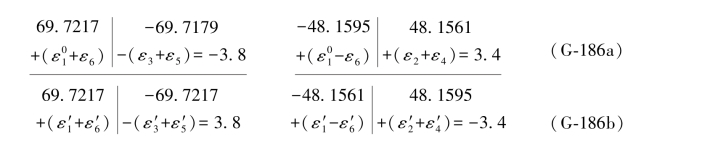
根据的(2-27)式知，若将误差距乘以-2.0，即可得到它们的双差和方程如下:

现在假设已经搜索到了58.9371，则有

根据“两项相等性质”，由(G-190c)式知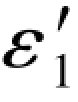，＝0.2、Δε6＝0.1，故有

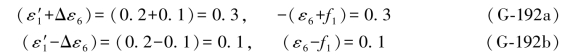
顾及Δε6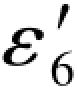＝-ε6，则(G-191c)又可写成如下形式:

上式中的2ε6是搜索值58.9371的真误差，而在(G-188)式中的ε6则是原观测值58.9406的真误差。

在(G-189b)式中给出了不同L6数值相应的双差和方程，现在利用这些双差和方程消去(G-188)和(G-192c)式中的2ε6，则有

根据“两项相等规律”，则有

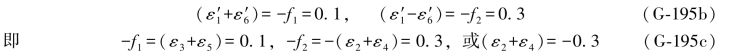
将上述结果代回(G-193c)式得:

为了进一步检核上述结果是否正确，还可以利用(G-173)各式。例如，由(G-173a)式得:

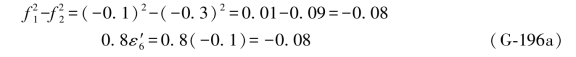
由(G-173b)式得:

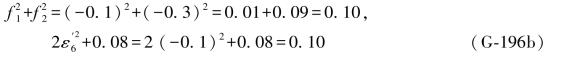
又由(G-173c)式得:

而由(7-7b)式可以查到:

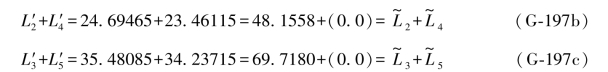
由原观测值可以算出:

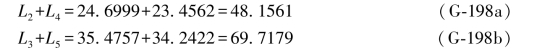
于是有:

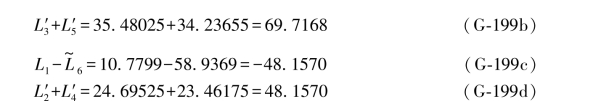
其余数据，例如L3+L5＝69.7179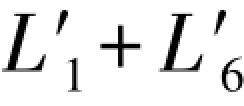，＝69.7179，L2+L4＝48.1561，以及L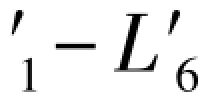＝-48.1561等，因数值没有改变，已在(G-184)、(G-185)各式中给出。类似于(G-186)式，可以写出以下两组条件方程:

(G-201c)式是误差距条件。由表3.6知，Δε1＝-1.0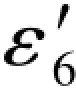，＝-0.1，根据“两项相等性质”应为:

将以上各值均乘以-2.0，即可得到各值的双差和方程，即

在以上各式中，f1，f2仍然是以(ε1+ε6)和(ε1-ε6)为主项的两个双环条件的副项。即

在(G-201c)式中的误差距条件中，若顾及Δε1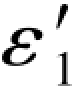＝(+ε1)，则(G-201c)式即可写成如下形式:

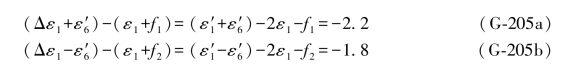
搜索对边真值的过程，实质上就是要使(G-206a)和(G-206b)两式变成

因为第3数值点上的(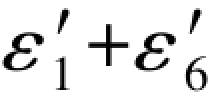)总是与第2数值点上的第1副项f1数值相等正负相反。因此

代入(G-208c)，得

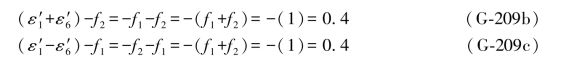
从以上推导可以看出，通过L6原观测值的双差和方程，可以消去(G-188)式中的2ε6，从而得到的结果均等于第1综合误差(1)的负值。如果是L6的搜索值，只要用该搜索值的双差和方程，照上述相同的做法，最后结果仍然是“0.4”，即仍然是-(1)。

根据“两项相等性质”，由(G-214c)式知:

在此情况下，对照(G-188b)和(G-188c)两式可以写出以下两式:

实际上，以上左、右两式就是误差距条件(G-214c)式中的左、右两式，除了58.9369之外，其他所有的搜索值都不可能使(G-215)式中的2ε6＝0.0，这是真值与非真值之间的一个原则性的区别。

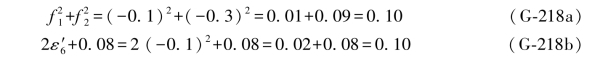
由(G-173c)式，得

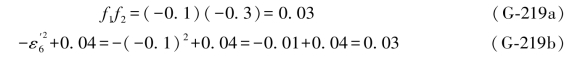
在实际计算中，以上3项检核，也可以只选用其中1项即可，不一定要全部算出。

由(7-7a)式知，

于是有:

(ⅲ)由表6.7知:

上面列举了不同的检核方法，其目的就是为了避免误判或发生计算上的错误，一定要保证结果的正确性。

于是由(G-175a)式得:

由(G-175b)式，得:

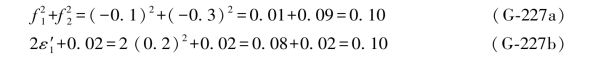
由(G-175c)式，得:

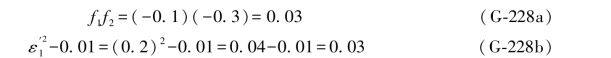
在实际计算工作中，可以只选用其中1项即可。其余检核项目均与前面所讲的相同，不再重复。

下面阐述有关2边、4边以及3边、5边的问题。因为主要思路都和1边、6边的相同，所以不再详细解释。

上述数值表明，每组中的4个数值点上的数值仍然符合前述的规律。在搜索过程中，第2、第3数值点上的数值一直保持不变。

如果(G-230)式写出真误差的表达式，则为

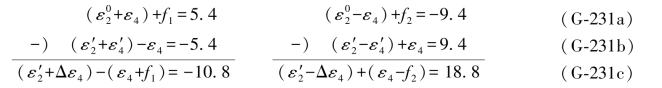
上式中，

从表3.2可以查到Δε4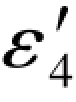＝-ε4＝-7.4，代入误差距条件(G-231c)式知，

于是根据“两项相等性质”知:

式中，ε4是L4原观测值23.4562的真误差。但必须注意，写成上述形式之后，它已经不再具有“两项相等性质”了，即

上述各值减去再生观测值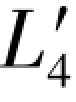＝23.4636，即可得到相应的误差距Δε4为:

将上述各值均乘以-2.0，即得相应的双差和方程常数项，即

若L4用原观测值的双差和方程消去(G-233a)和(G-233b)中的2ε4，则有

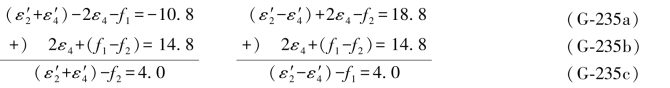
由(G-231a)和(G-231b)可以看出(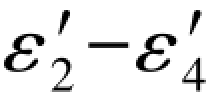)和(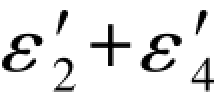)应分别于第2数值点上的f1、f2数值相等正负相反。因此，由

误差距条件(G-237c)式仍然符合“两项相等性质”，即

从表3.4中可以查到Δε2＝2.8，故(Δε2+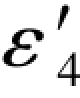)＝(2.8-6.9)＝-4.1，(Δε2-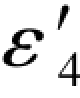)＝(2.8+6.9)＝9.7，因此，(G-239c)式中的该误差距条件仍然符合“两项相等性质”的规律，即

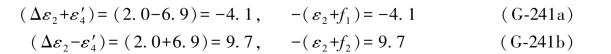
如果顾及Δε2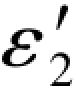＝-ε2，代入(G-239c)式，则可写出以下两式

上述各值与再生观测值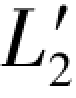＝24.6971相减即得误差距Δε2，

上述各值均乘以-2.0，即得双差和方程为:

于是可以进行以下各项检核:

(ⅰ)由(G-177a)式得:

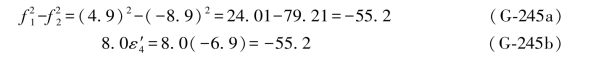
由(G-177b)式得:

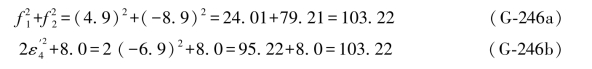
又由(G-177c)式得:

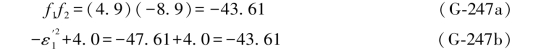
上述检核可以只选用一项即可。

由(F-49b)式知:

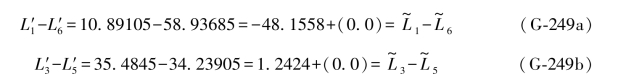
由原观测值还可以算出以下结果:

于是有:

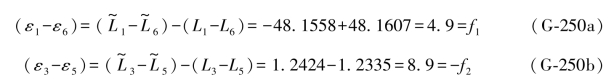
而由表1.1知，原始的观测误差距向量为:

两式相减得:

上式中第2、第4个数值实际上就是ε2＝-0.8和ε4＝0.5，而第1、第6个数值则分别是:

第3、第5个数值则分别是

若须进行前面所讲的第(ⅰ)项检核，则须应用(G-176)各式。例如，由(G-176a)式得:

由表3.3知，Δε3＝3.8，代入(G-156c)的误差距条件，则有

故有

上式表明，误差距条件一定满足“两项相等性质”这一规律。考虑到Δε5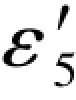＝-ε5，则(G-256c)式可以写成如下形式:

将以上各值与再生观测值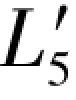＝34.2384相减，即得相应的误差距Δε5，即

再将误差距乘以-2.0，即可得各观测值的双差和方程为:

根据“两项相等性质”，由上述误差距条件(G-260c)式可得:

实际上，(G-160)式也可写成如下形式:

上式中的副项f1和f2仍然未变，即如(G-256d)式所示。

从表3.5中可以查到Δε3＝-6.4，于是由误差距条件(G-264c)式知:

于是有

上式表明，误差距条件(G-264c)式仍然满足“两项相等性质”。

顾及Δε3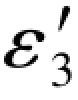＝-ε3，代入(G-264c)式，则可得到以下两式:

上述各值与再生观测值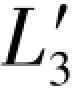＝35.4821之差即为其误差距Δε3，即

以上各值均乘以-2.0，则为其双差和方程，即

由(F-53b)式知:

由原观测值知:

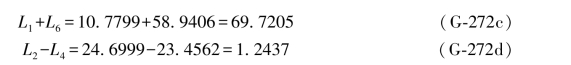
于是有:

(ⅲ)由表6.7知:

第2、第4个数分别为:

以上就1、6，2、4以及3、5三种互为对边的情况，推导了它们由一真向量转变成双真向量时数值的变化规律。必须说明的是，所有推导的数值结果都是针对图形D以及表1.1中所列出的6个原观测值而导出的，因此，如果不是图形D，或者即使是同一个图形，但6个原观测值改变了，那么，所有结果也都随之改变。下面将就针对这一特定条件，来讨论搜索3对边真值时应该满足的条件。

顾及(G-194c)式，误差距条件(G-278c)式仍具有“两项相等性质”，即

与此同时，(G-188b)和(G-188c)式已经变成如下形式:

以上两式是双环条件中第1、第2两个副项f1、f2的函数。因为只有在双真向量情况下，双环条件闭合差F1、F2就分别等于f1、f2，所以(G-281a)式也可写成:

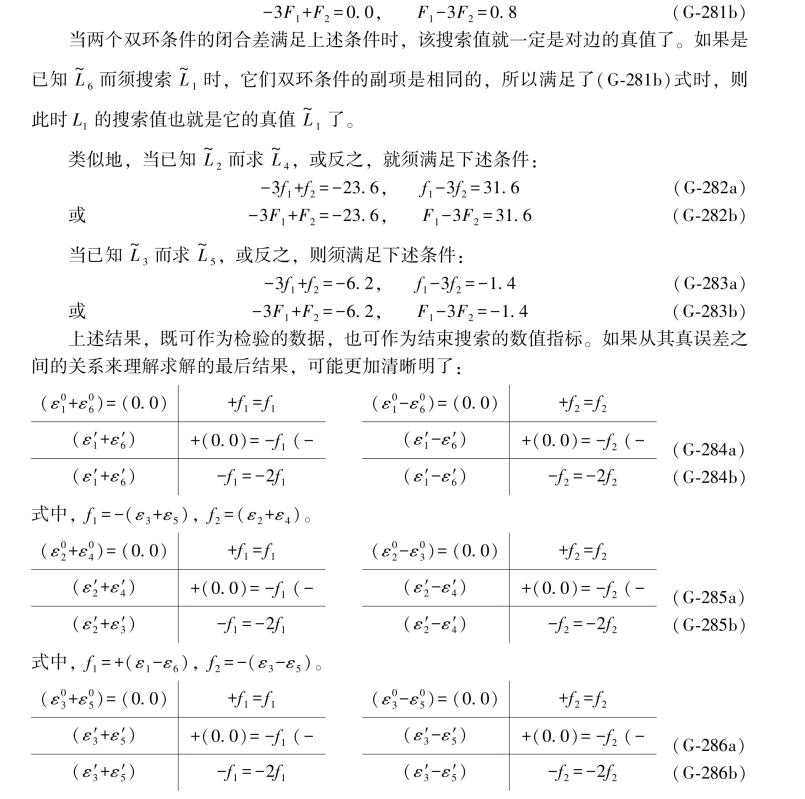
式中f1＝-(ε1+ε6)，f2＝-(ε2+ε4)。

以上所有各组条件中，其中第2、第3数值点上的数值自始至终完全没有变动过，而最后的解就反映在误差距条件中。如果最后解得结果不满足以上误差距条件的3个式子，那就是错误的解。实际上，以上3组式子在前面也都已经出现过，但是考虑到，它们的误差距条件对于理解什么才是真解有着重要的意义，因此，再次集中地写在上面，以便于对照和比较。

当对边真值确定之后，双环条件的两个副项f1和f2也都随之确定，然后就可以按照附录D中所介绍的“同步改化与同步观测值”，进而求出其余4个(伴随)观测值的真值。