(E-1b)式是(E-1a)式的再生向量。(E-1a)式的真误差向量应为:

由此列出的6个双差和方程为:

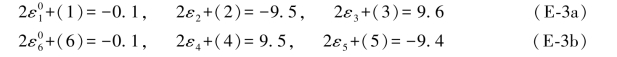
根据(E-1d)式并对照表6.7中的综合误差公式，即可写出上述双差和方程中各个综合误差的具体表达式为:

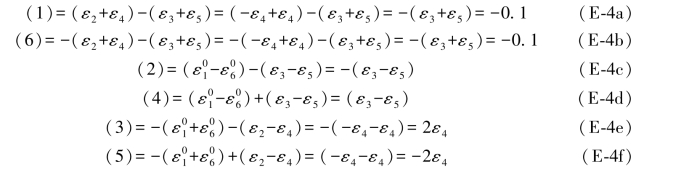
将以上各综合误差均乘以-0.5，即得相应的再生真误差为:

由以上推导可以得到如下结论:

由上式列出的6个双差和方程为:

①对于图形D而言，由其原观测值列出的4个(伴随)双差和方程为(表1.1):

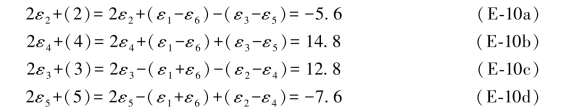
在(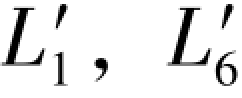)混合向量情况下，这4个(伴随)双差和方程应为(见(7-35a)式和(7-35b)式):

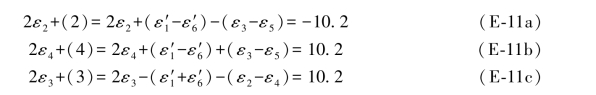
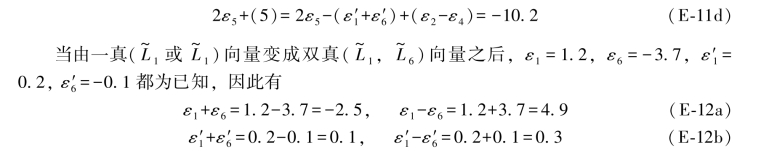
将上述数值代入(E-10)和(E-11)各式，即可得到以下结果:

因而，双差和方程应为:

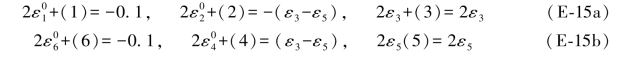
与此相对应的观测向量的真误差矩阵表达式应为:

(E-2)各式中所给出的数值是相当于用(24.6994，23.4564)这一对同步观测值时所得到的结果，不难看出，3个条件的闭合差依次为-0.1，0.0，-9.5。6个双差和方程则如(E-3a)式和(E-3b)式所示。为了检验这一对同步观测值是否就是真值，要利用(E-13a)和(E-13b)两式作为参考值。

下面分析相减的结果是代表着什么数值。例如，第2个双差和方程和参考值是2ε2+(2)＝2ε2-(ε3-ε5)＝-10.5，而由同步观测值求得的结果则依次与(E-16)式中的数值相同，前者与后者相减得:

同样地，用(E-13)式中的参考值对应相减得:

(www.daowen.com)

这里需要强调的是，仅仅通过搜索而要将双差和方程正确地分解成2εi和(i)之和，显然是无法得到唯一解，因为由(E-17)式可以看出，其中-1.6-8.9＝-10.5，事实上，其余所有上下对应的两个数同样满足这一要求，例如，-1.4-9.1＝-10.5，-1.2-9.3＝-10.5，依次类推。真正需要的解是在两个同步观测值的真误差必须同时等于零时的解，而不是其他任意的一个解。为此，就要提出“异号组合”的概念。在表6.4中列出了图形D分别以(ε1、ε6)、(ε2、ε4)和(ε3、ε5)为主要误差对的三种情况，在第1组中，是以(ε1+ε6)和(ε1-ε6)为主项的3个双环条件，-(ε3+ε5)是(ε1+ε6)的副项，(ε2+ε4)是(ε1-ε6)的副项，而在第3个双环条件中，(ε2-ε4)是(ε2+ε4)的“异号组合”，因为它们中的ε2为同号，均为正，但ε4则为一正一负，因此，称(ε2-ε4)是(ε2+ε4)的“异号组合”。同样地，(ε3-ε5)是(ε3+ε5)的异号组合。表6.4中第2组是以(ε2+ε4)和(ε2-ε4)为主项，(ε1-ε6)和(ε3-ε5)是两个副项，而在第3个条件中，(ε1+ε6)是(ε1-ε6)的异号组合，(ε3+ε5)则是(ε3-ε5)的异号组合。表中的第3组同样如此，(ε3+ε5)和(ε3-ε5)为主项，(ε1+ε6)和(ε2-ε4)为副项，而第3个条件中的(ε1-ε6)是(ε1+ε6)的异号组合，(ε2+ε4)是(ε2-ε4)的异号组合。

在上式中，ε2＝-0.8保持不变，ε4则由0.5逐渐改变到-0.5，于是得到一系列和数，(E-23)式中的首项为(ε2+ε4)＝-0.3，末项即为(ε2-ε4)＝-1.3，首项与末项相加或相减，即得:

由此列出的6个双差和方程为:

(E-24a)式的真误差向量应为:

式中，ε3已换成-ε5(见(D-5a)式)。对照表6.7即可写出(E-26)式中各双差和方程中综合误差的具体表达式为:

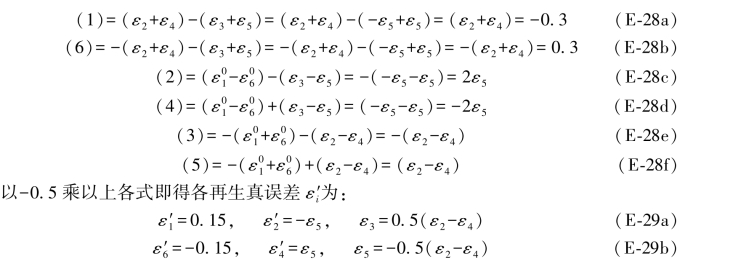
从以上结果可以看出，(1)与(6)为已知的常数0.3或-0.3，(2)与(4)只与ε5有关，(3)与(5)是一确定的常数(ε2-ε4)，或正或负。

除了第1、6两个双差和方程常数项仍保持不变之外，第2、4两个双差和方程的常数项分别等于2ε2和2ε4，即等于ε2与ε4的两倍，而第3、5两个双差和方程的常数项等于(ε2-ε4)，或正或负。

对于L3、L5的同步观测值而言，(ε3+ε5)＝(-ε5+ε5)＝0.0，即(ε3+ε5)恒为零，但它的异号组合(ε3-ε5)在尚未搜索到真值之前，ε3与ε5均不等于零，故其异号组合(ε3-ε5)＝(-ε5-ε5)＝-2ε5≠0.0。但随着同步观测值的变化，它们的真误差将如(D-8)式所示，由最初的(4.4，-4.4)逐个在缩小，直到(0.0，0.0)为止。例如，在(E-24a)式中用的是第一组同步观测值(35.4758，34.2422)，它的真误差为(4.4，-4.4)，所以(ε3+ε5)＝0.0，但(ε3-ε5)＝-2ε5＝8.8，代入(E-25c)式，得:

这里需要指出的是，虽然从理论上说，无论是用L2、L4还是用L3、L5的同步观测值进行搜索，其最后结果，都能同时得到4个(伴随)观测值的真值，但搜索的过程显然是L2、L4比较快速，这一点在实际计算时还是应该予以考虑的。

④由上述讨论可以知道，将互为对边的观测值进行同步改化的目的就是要使真误差不等的两个观测值改化成真误差数值相等的观测值，这样就可以同时对一对观测值进行搜索。例如，(L2，L4)的同步观测值真误差为(ε2，ε4)＝(-0.5，0.5)(见(D-11)式)(L3，L5)的同步观测值真误差为(ε3，ε5)＝(4.4，-4.4)(见(D-8)式)。这些数值则是通过模拟的真值求得的，事实上，这些真值都是未知的，因此，通过同步改化之后只知道真误差一定数值相等，但具体数值大小，实际上是未知的。这正是实际搜索中的困难所在，那就是一对搜索值正好是真值时，搜索应到此停止，不再往下搜索。在(E-4a)到(E-4f)诸式中，给出了尚未搜索到真值时的综合误差公式，其中(1)和(6)是一确定不变的常数-0.1，不必考虑，问题是4个(伴随)综合误差的公式，由这些公式即可写出(E-3a)式和(E-3b)式中6个双差和方程。由于在(E-1a)式中所用的同步观测值(24.6994，23.4564)还不是真值，所以在第2、4两个双差和方程中的2ε2≠0.0，2ε4≠0.0，而在第3、5两个双差和方程中，综合误差(3)和(5)中都还包含有2ε4或-2ε4，它们也不等于零。随着搜索的不断进行，每更换一次同步观测值，则ε4减小0.1，但2ε4则减小0.2，直到2ε4等于零时，即表示已经找到了真值。因此，也可以将搜索描述成在逐步减小ε4的数值直到等于零时为止。于是可以将4个(伴随)双差和方程写成:

这样，每一个双差和方程就成为两个单环条件的不同组合，例如，第2个双差和方程是由第4单环条件与第2单环条件组合而成，第3个双差和方程是由第3单环条件与第2单环条件组合而成，等等。而且在每个单环条件中只包含一个数值改变的真误差，即ε2或ε4，另一个则是数值始终不变的真误差，即ε3或ε5。因为在搜索时，是采用同步观测值，此时ε2＝-ε4，于是(E-34)中各式又可写成如下形式:

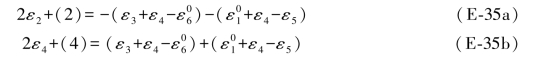
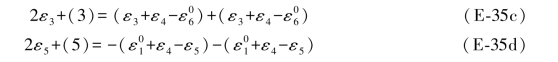
每替换一次同步观测值，就列出与上述有关单环条件，举例来说，在(E-1a)式中是用同步观测值(24.6994，23.4564)构成的向量，由该式可列出单环条件为:

代入(E-35)各式可得:

代入(E-35)各式得:

由上式又可列出6个双差和方程为:

至此，图形D的真值向量为: