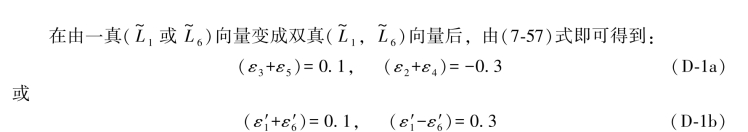
根据表7.3中(7-46b)式可以求得L3与L5以及L2与L4的真值之和为:

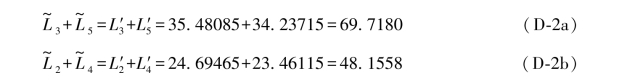
尽管ε3+ε5＝0.1已知，但究竟ε3和ε5真正的数值等于多少还是未知的。由于已知ε3为正，ε5为负，所以(ε3，ε5)一定是下述一系列数组中的一个，即

同样，由于ε2+ε4＝-0.3，且已知ε2为负，ε4为正，所以(ε2，ε4)一定是下面所给出的数组中之一，即

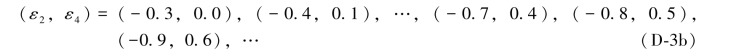
如果利用(D-3a)式中各数组分别对原观测值L3和L5进行改正，例如，35.4757+(0.1)＝35.4758，34.2422+(0.0)＝34.2422，又例如35.4757+(0.2)＝35.4759，34.2422+(-0.1)＝34.2421，…，依次类推，于是就得到了一系列不同的数值组合，即

由以上推导可知，经过改正后的观测值，不仅仅它们之和一定等于相应真值之和，而且它们的真误差一定是数值相等而正负相反。

其余依次类推。

由以上结果可以看出，经过改正后的观测值具有两大特点:第一，改正后的互为对边观测值之和一定等于其真值之和；第二，互为对边的观测值，其真误差一定是数值相等而正负相反。因此，在搜索其真值时，就不必一个个地搜索，而是可以一对对地搜索。随着搜索的进行，其真误差也在不断地减小，直到两个真误差同时等于零时为止。对于(L3，L5)而言，其真误差的变化应该是如(D-8)式所示:

由上述推导可见，经过改正后的观测值，其真误差相等，正负相反，因此称之为“同步观测值”，(D-4a)式、(D-4b)式中的观测值都已经是“同步观测值”。而将原真误差不相等的两个原观测值进行改正从而得到“同步观测值”，则称之为“同步改化”。

这里需要指出的是，在求同步观测值的真误差时，是引用了模拟的真值。但实际情况是，真值是客观存在的，但在未求解出来之前还是未知的，这里之所以引用模拟真值，只是为了说明同步观测值的性质和特点。

顺便提出，对于每个观测值都有两个特殊值，而且互为对边的两个观测值，它们特殊值的真误差也是很有规律的。从表7.5可以看出，L1和L6的特殊值10.7810和58.9368的真误差都等于(ε3+ε5)(或为(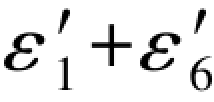))，而另一个特殊值10.7808和58.9372的真误差则是分别等于-(ε2+ε4)(或为(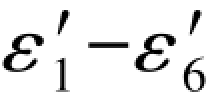))和等于(ε2+ε4)(或为-(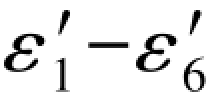))，也就是说这两个特殊值的真误差数值相等而正负相反，于是可以写出该数组及其真误差数组应如下式所示:

(D-15)各式是等值双环条件，其闭合差与(D-14)各式均相等。由以上各式知:

虽然ε1-ε6＝4.9和ε3-ε5＝8.9都是已知的，但ε1和ε6以及ε3和ε5究竟等于多少还是未知的，因为ε1-ε6＝4.9，故有ε6＝ε1-4.9，已知ε1为正，ε6为负，于是ε1与ε6一定是下列数组中的一个，即(www.daowen.com)

已知L1的原观测值为10.7799，L6的原观测值为58.9406，利用(D-21)中各数组进行同步改化，于是有

又例如，

依次类推，于是可以得到下述一系列的数值组合:

同样地，因已知ε3-ε5＝8.9，故有ε5＝ε3-8.9，且已知ε3为正，ε5为负，由此即可得到下面一系列有关(ε3，ε5)的数组，即

已知原观测值L3＝35.4757，L5＝34.2422，用上述数组分别进行同步改化，即可得到下列同步观测值数组:

又由第2组得:

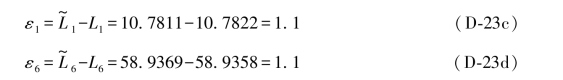
其余依次类推，于是各对同步观测值的真误差应为:

同样，可以求得(D-22b)式中各对同步观测值的真误差:

对于第2组，则为:

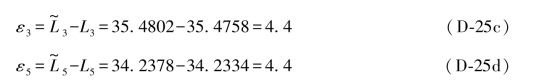
依次进行计算，即可得到各对同步观测值的真误差为:

由(D-24)和(D-26)两式可以看出，各对同步观测值的真误差不仅数值相等，而且正负同号。这是因为这里两个副项(ε1-ε6)和-(ε3-ε5)都是两个真误差之差，而在(D-1a)和(D-1b)两式中，两个副项(ε3+ε5)和(ε2+ε4)都是两个真误差之和，所以每对同步观测值的真误差都是数值相等，但正负相反。

经过以上讨论的两种情况，可以得到一个普遍的规律，即副项是两个真误差之和，其同步观测值的真误差就应数值相等，正负相反；若副项是两个真误差之差，则其同步观测值的真误差就应是数值相等，正负相同。