3(或5)边已知，求对边与其他边的高差真值

图7.11　L5特殊值矩形图

图7.12　L5特殊值矩形图坐标轴示意图

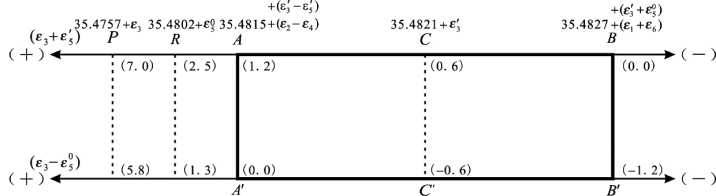
图7.13　L3特殊值矩形图

图7.14　L3特殊值矩形坐标轴示意图

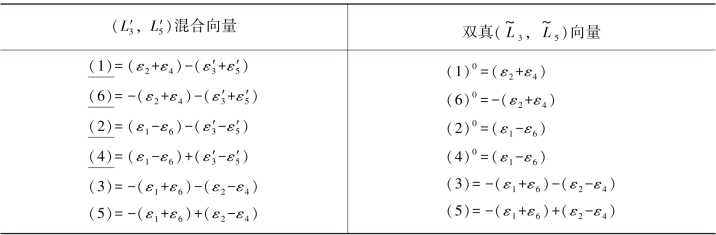
表7.9　图形D双真(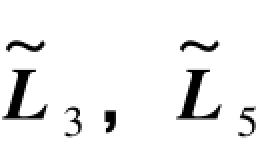)向量情况下公式汇编

在表7.9中以不同“基数”表达的4个(伴随)双差和方程，是指由原观测向量列出的双差和方程(见表1.1)，另一个是指由(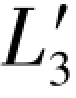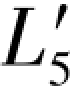，)混合向量所列出的双差和方程(见附录(C-6a)与(C-6b)式)。

表7.10　图形D不同情况下的综合误差公式

由(7-93a)式列出的双差和方程为:

在搜索的过程中，必须进行以下多种检验，以确定该搜索值是否就是对边的真值:

因此，(7-94c)式就可以写成如下形式:(Δε3)1和(Δε3)2分别是由35.4827和35.4815求得的误差距，它们等于已知的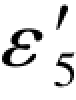，一正一负。

将(7-102b)式和(7-102d)式中的(ε1+ε6)＝-2.5和(ε2-ε4)＝-1.3代入以上各式，即可求得:

通过上述双差和方程的检验得到同样的结果。(https://www.daowen.com)

根据附录D中所介绍的同步改化法，对(L1，L6)和(L2，L4)进行改化。因为由误差距可以判断ε1为正，ε6为负，ε2为负，ε4为正，所以对于(ε1+ε6)＝-2.5而言，(ε1，ε6)一定是下列各数组中之一，即

对于(ε2-ε4)＝-1.3而言，则(ε2，ε4)一定是下列各数组中之一，即

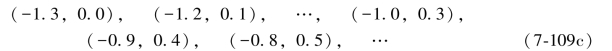
利用以上数组分别对原观测值(L1，L6)和(L2，L4)进行改正，于是得到以下同步观测值组合:

(7-111a)式的真误差向量应为:

其中，ε6＝-ε1，即同步观测值L1与L6的真误差数值相等，正负相反。

由(7-111a)式列出的双环条件为:

6个双差和方程为:

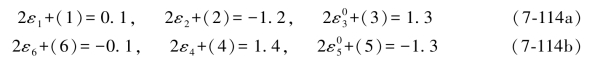
根据表6.7中的综合误差公式，并对照(7-112)式，即可写出上式中各综合误差的具体表达式如下:

由(7-122a)式列出的双环条件及双差和方程为:

(7-122a)式的真误差向量应为:

(7-125a)式中ε2＝ε4，即同步观测值L2的真误差与L4的真误差数值相等，正负同号。根据表6.7中的综合误差公式并对照(7-125a)式，即可写出(7-124)各式的综合误差的具体表达式为:

由(7-126a)式列出的双环条件和双差和方程分别为:

这种对两对同步观测值同时进行的搜索称为“双向搜索”。一般而言，只要进行“单向搜索”就可以了，但进行“双向搜索”当然可以起到相互检核的作用。