在7.2节中对已知1边或6边真值的情况下如何求解其余各边真值的问题作了详细的讨论和阐述，如果是2边或4边的高差真值为已知，而要求解其余各边的真值，所涉及的理论与方法应该是相同的，只是个别地方与7.2节不同，为此，本节将对不同之处予以提出，相似之处将不再重复叙述。

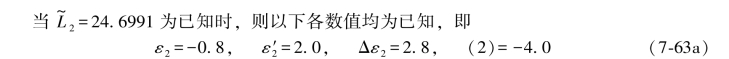
除此之外，以下数值也都是已知的，即

其中，23.4562是L4的原观测值，23.4616和23.4656是L4的两个特殊值，23.4636是L4的再生观测值。

首先要通过搜索求出对边L4的真值，因已知ε4为正，假设采用以下一系列搜索值:

在(7-65a)和(7-65b)两式中，所有上下对应的闭合差之和均等于-4.0，实际上就是L2的综合误差(2)，此外，对应于两个特殊值的闭合差分别是(0.0，-4.0)和(-4.0，0.0)，它们都是一个闭合差为零，另一个为非零，等于-4.0。(7-65c)式是第3个双环条件，因为该条件中不包含ε2与ε4，故其闭合差始终等于-2.6，它不因L2与L4的变动而受到影响。

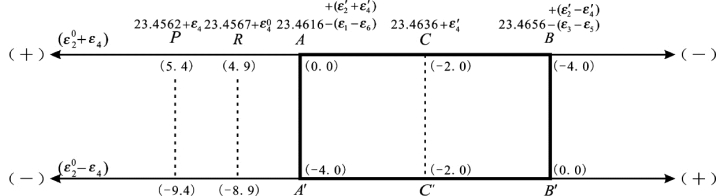
图7.7　L4特殊值矩形图

图7.8　L4特殊值矩形图3个坐标轴示意图

在(7-68a)和(7-68b)两式中，上下对应的闭合差之差均等于13.8，也就是等于L4的综合误差(4)，数组(0.0，-13.8)和(13.8，0.0)则是对应于两个特殊值所产生的闭合差，其中一个为零，另一个为非零，等于13.8或-13.8，(7-68c)式中的第3个双环条件，因其中不包含ε2与ε4，故其闭合差均等于-2.6，保持不变。

图7.9　L2特殊值矩形图

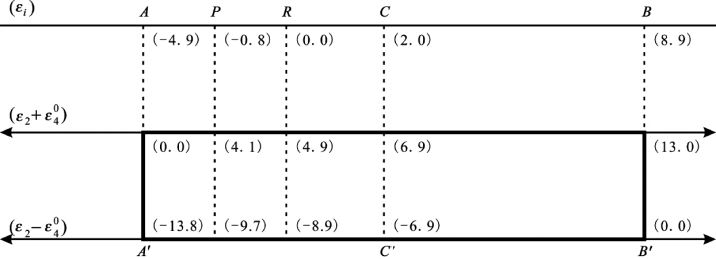
图7.10　L2特殊值矩形图坐标轴示意图

表7.7　图形D双真(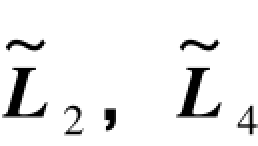)向量情况下公式汇编

续表

此外，还可列出6个双差和方程为:

表7.8　图形D在不同情况下的综合误差公式

于是，由(7-73d)和(7-73e)中各式得:(www.daowen.com)

于是，(7-72c)式变成:

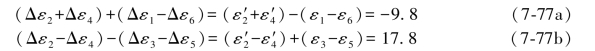
根据表7.4中的等值关系式，由上式可得:

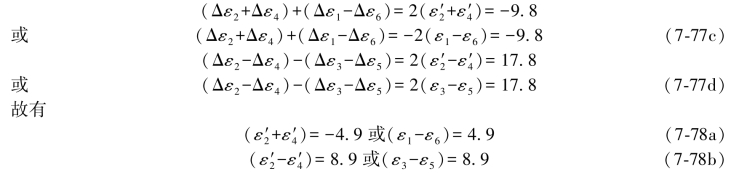
上述结果与(7-75a)和(7-75b)式中的结果相一致，所以说明当前所用的搜索值已经是真值。

其真误差向量为:

根据误差距定义式Δε4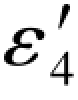＝-ε4可以分别求得:

(Δε4)1和(Δε4)2分别是由(7-79a)式和(7-79c)式求得的误差距，其结果均等于2边已知的再生真误差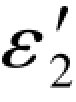，或正或负。

由此，求得的误差距分别为:

(Δε2)1和(Δε2)2是分别由(7-80a)和(7-80c)式求得的误差距，其结果均等于4边已知的再生真误差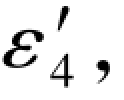或正或负。

有了同步观测值之后，即可进行搜索，既可以用(L1，L6)也可以用(L3，L5)的同步观测值，假设是用(L1，L6)的同步观测值，并假设已经搜索到(10.7810，58.9368)，则有

并可列出6个双差和方程为:

上式中，(2)、(4)、(1)、(6)均与(ε3，ε5)有关，而(ε3，ε5)都是原真误差，不受搜索的影响，所以这些都是固定不变的常数，而(3)与(5)则随同步搜索值的改变而改变。

由(7-88a)式列出双环条件为:

以及6个双差和方程为:

上述向量与表1.1中的模拟真值完全相等，对于实测的水准测量而言，这就是所施测的各地面点间的高差真值。