除此之外，下面几个数值也同样是已知的，即

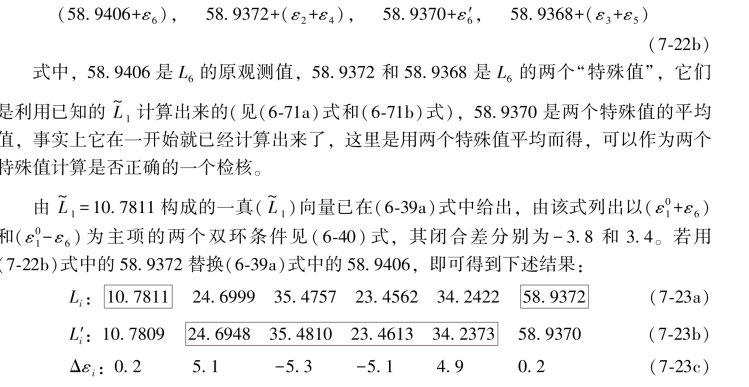
同样，将(7-22b)式中的58.9406替换成58.9368，所列出的两个双环条件，在(6-64d)中也已经给出，即

假设按(7-22b)式中的顺序，写出它们的双环条件的闭合差则为如下结果:

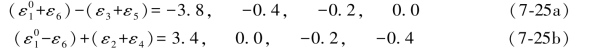
以上4个结果是求解6边真值时非常重要的参考值，其中一个是6边的原观测值，两个是6边的“特殊值”，另外两个是特殊值的平均值也就是6边的再生观测值。

为了能清晰便捷地看出它们之间变化的规律性，现将这些数值表示在图上(图7.1)。

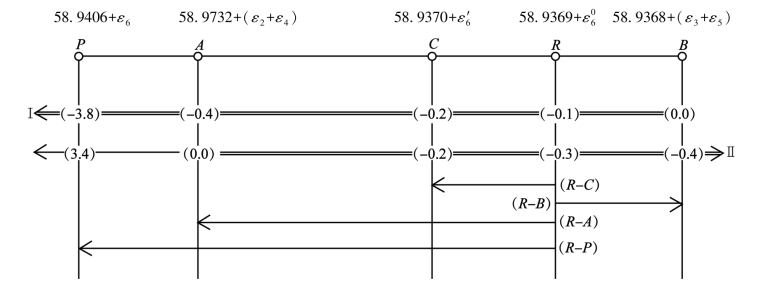
图7.1　与L6有关的重要数据示意图

在图7.1中，P点是6边的原观测值，A点和B点是L6的两个特殊值。C点是AB的中点，也是6边的再生观测值，R点是6边的真值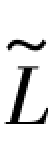6。

除了R点是后来求得的，其余的P、A、B、C4点都是已知的。在图中的(I)线上，从右方的(0.0)开始向左为(-0.2)、(-0.4)和(-3.8)，实际上，前者即为(7-25a)式中的各闭合差，后者则为(7-25b)式中的各闭合差，而且两条线上的数值均为负值。

由表6.7查到综合误差(1)和(6)的公式，并将上述有关数值代入得

若将(7-29a)式中的10.7808替换成10.7810，并由该式列出两个双环条件，即可得到以下结果:

为了清晰起见，将上述数值表示在图7.2中，图中所用英文字母符号仍与图7.1相同。

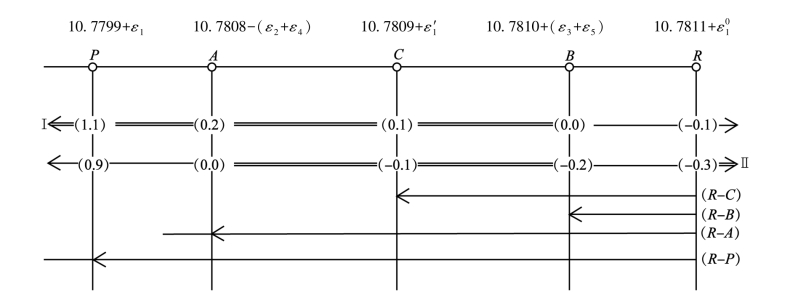
图7.2　与L1有关的重要数据示意图

(7-7b)式是(7-7a)式的再生向量，(7-7c)式是误差矩向量。

(7-7a)式和(7-7b)式以及它们的真误差矩阵表达式应为:

式中，综合误差表达式列在表6.7中，为了便于比较，现将它们转抄于表7.2内的第一列。

由(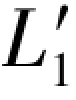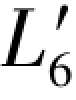，)混合向量列出的3个双环条件方程已在附录A中给出(见(A-5)各式)，并在(A-6a)、(A-6b)两式写出了它们的6个双差和方程，即

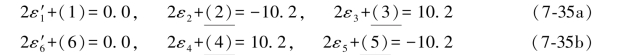
表7.2　图形D在不同情况下的综合误差公式

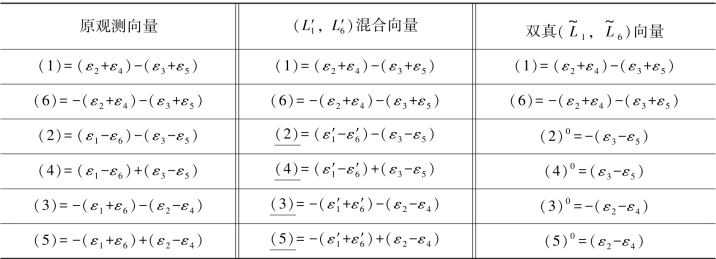
由以上各式即可写出相应的双差和方程，例如，由(7-38a)式可以写出:

按同样方法即可得到以下各式:

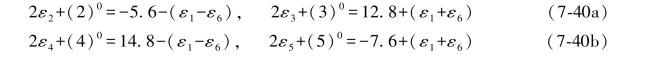
以及

除了上述一些条件之外，在此基础上还可以对综合误差公式以及误差距的和与差等公式作相应的改变，例如，综合误差(1)和(6)可写成:

顺便指出，(Δε2-Δε4)和(Δε3-Δε5)因与ε1、ε6无关，所以它们仍然等于10.2或-10.2，没有变化。

为了往后查阅和应用方便，现将以上导出的有关公式均汇集于表7.3内。

表7.3　图形D双真(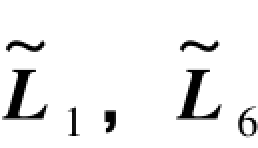)向量情况下公式汇编

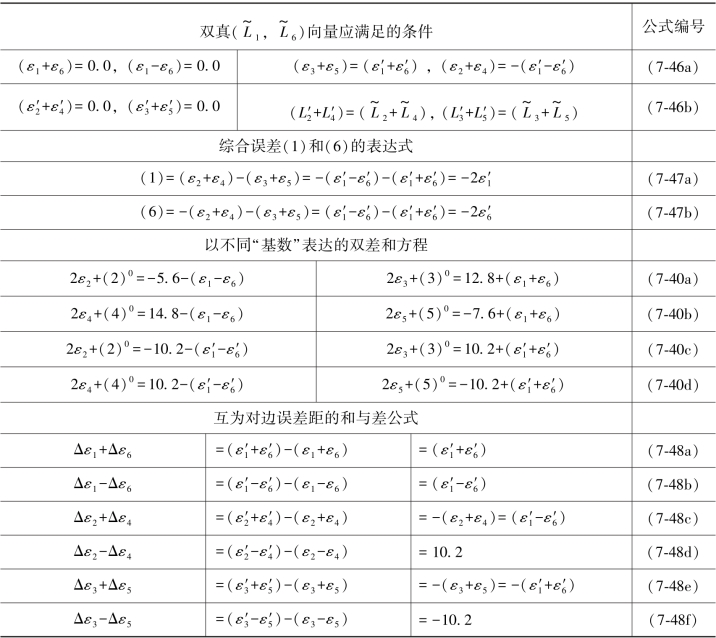
由(B-3a)和(B-3b)式得:

由(C-3a)和(C-3b)式得:

对于图形D而言，以上等式是一定成立的，是固定不变的，因此称以上各式为图形D的“等值关系式”。对于不同的典型图形，同样都有各自的“等值关系式”。利用这些关系式，就可以将原来的双环条件改变成另一种形式。例如，在表6.4中以(ε1+ε6)为主项的双环条件为(ε1+ε6)-(ε3+ε5)＝-2.6，其中-(ε3+ε5)是(ε1+ε6)的副项，利用等值关系式，就可写成:

(www.daowen.com)

同样的，以(ε1-ε6)为主项的双环条件，它的副项为+(ε2+ε4)，利用等值关系式，就可以写成:

为了便于区分，以后将(7-50a)式求和(7-50b)式中的双环条件称为以(ε1+ε6)和(ε1-ε6)为主项的“等值双环条件”。为了便于往后查阅，现将有关公式汇集于表7.4内。

表7.4　图形D等值关系式及等值条件式

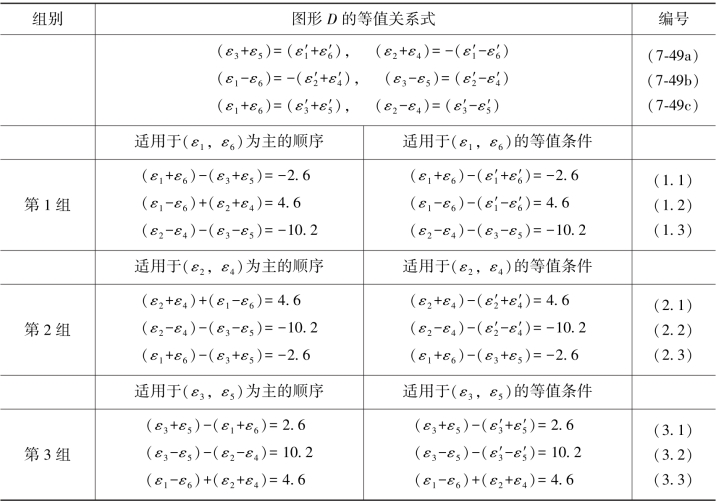
下面将提出与寻找真值有关的非常重要的几个概念性问题:

②真值的搜索方向与真误差的变化。原真误差εi的正负号是与其误差距Δεi的正负号相反，故当原真误差εi为正时，其搜索值则应比其原观测值大，反之亦然。但必须注意，当搜索值逐渐增大时，它的真误差εi则在逐渐减小，直到搜索值刚好等于真值时，真误差等于零。同理，若原真误差为负，则其搜索值应逐渐减小，此时搜索值的真误差的绝对值也在随之减小，直到搜索值正好等于真值时，真误差也正好等于零。由此可见，无论原真误差是正还是负，随着搜索值的改变，其真误差的绝对值都是越来越小，直到等于零为止。

④真值所处的位置。如果原观测值的真误差εi为正，它的再生真误差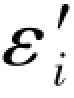也为正，那么在搜索过程中所有搜索值的真误差一定也为正，只不过是数值越来越小而已，在此情况下，只有当搜索值大于再生观测值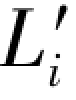时才有可能出现真值，因此，真值是在原观测值与再生观测值这一区间之外。同理，若原真误差为负，它的再生真误差也为负，那么搜索值的真误差的绝对值将越来越小，只有当搜索值小于其再生观测值时，才会出现其真值，在此情况下，真值同样是落在原观测值与再生观测值这一区间之外。如果原真误差为正，而其再生真误差为负；或者反之，那么搜索值的真误差必定是由正变负或反之，因此，在这种情况下，真值一定是落在原观测值与再生观测值这一区间之内。如果以图形D为例，6个双差和方程的数据如下所示:

(7-52b)式中ε6就是搜索值58.9376的真误差。现在利用(7-52b)中两式对该搜索值进行真误差置换，也就是要使58.9376的真误差置换成(ε6+0.8)和(ε6+0.4)。根据真误差置换法可得:

(7-53a)式和(7-53b)中58.9368和58.9372实际上就是L6的两个特殊值(表6.5)，而(ε6+0.8)和(ε6+0.4)分别是这两个特殊值的真误差，顾及(7-52b)式，则以上两式也可写成如下形式:

表7.5　各类结果汇总

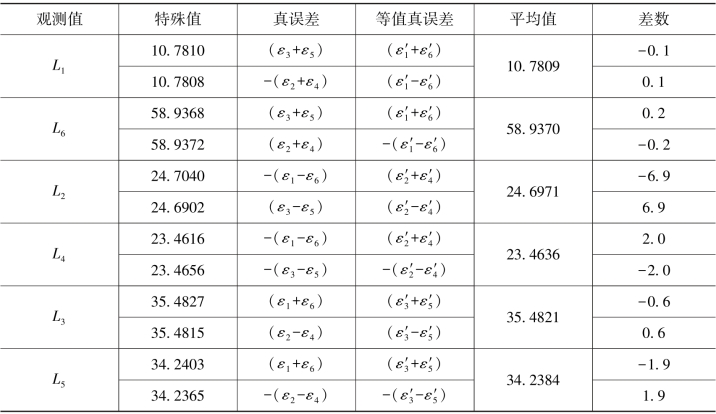
从以上两个例子可以看出，无论搜索值等于多大，通过双环条件闭合差和真误差置换都可以将它归化成它的两个特殊值，即58.9368和58.9372。因此，在搜索对边真值时，能够起到重要作用的是对边的原观测值和再生观测值以及该边的两个特殊值。

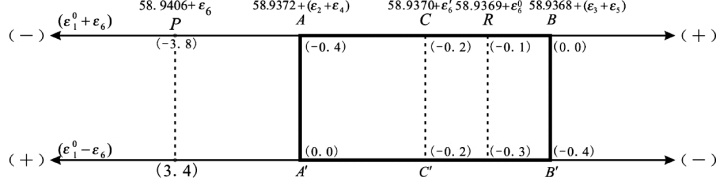
图7.3　L6特殊值矩形图

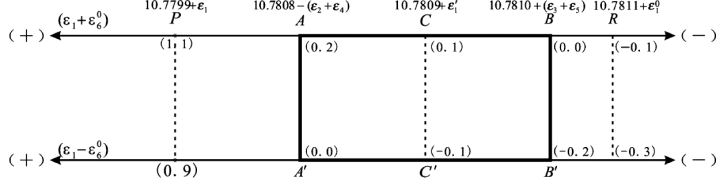
图7.4　L1特殊值矩形图

因此，当双环条件的闭合差正好等于-0.1和-0.3时，就表示L1和L6都已经是真值。

以上通过已知的模拟真误差值说明了互为对边的两个特殊值矩形图在P、A、C、B各个点上数值之间的关系。事实上，在真值求出之前，这些真误差值都还是未知的，因此，就要解决如何根据双环条件的闭合差来判别是否已经搜索到了对边的真值。

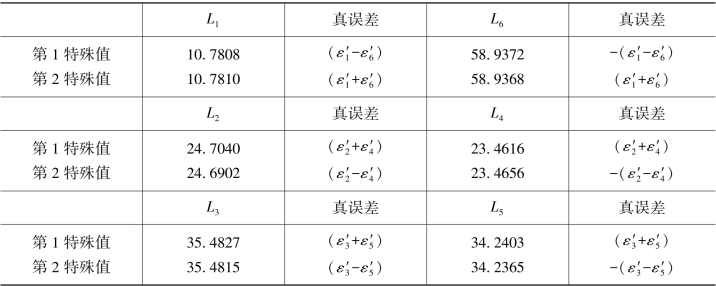
为了便于比较互为对边的两个特殊值真误差之间的关系，现将它们一并列在表7.6内。

表7.6　图形D各边特殊值及其真误差表达式

实际上，以上两式在表6.12中就已经给出(表6.12中的(7-47a)式和(7-47b)式)，以上两式也可以称为“等值综合误差公式”。

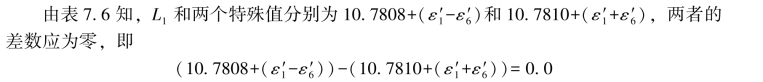
由上式并对照(7-60b)式即可得到:

由上式并顾及(7-60a)式，则有

由以上推导得到一个结论:即某一观测值的两个特殊值之差就等于其对边观测值的综合误差，换句话说，L1的两个特殊值之差就应等于其对边L6的综合误差(6)，反之，L6的两个特殊值之差就应等于其对边L1的综合误差(1)。

以上提出了一系列的概念性问题，都是真误差解析法中的一些基础理论，实际上，其中有些问题在前几章中就已陆续提出过，这里只是重复一下而已。

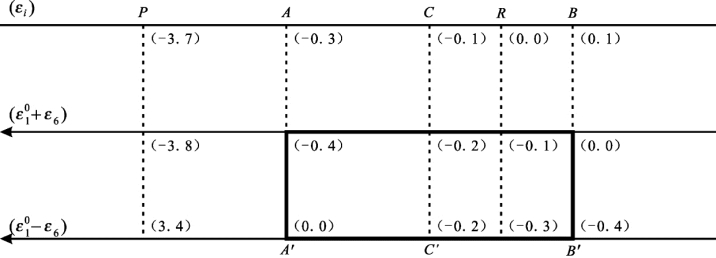
图7.5　L6特殊值矩形图坐标轴示意图

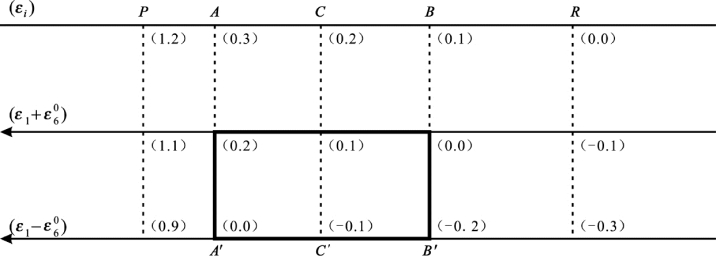
图7.6　L1特殊值矩形图坐标轴示意图

当对边真值求出以后，就可以根据附录D和E中所提出的同步改化法对互为对边的(伴随)观测值进行改化，并利用同步观测值进行搜索，从而得到所有(伴随)观测值的真值，有关具体做法已在附录中介绍，这里不再重复。