有关图形D的公式在前面几章中都已陆续给出，为了往后查阅更为方便，同时也是为了从中看出各种公式之间的关系，现将有关公式分别汇总于表6.6，表6.7，表6.8，表6.9中。

表6.6　图形D互为对边高差真值之和与差

表6.7　图形D互为对边综合误差公式

表6.8　图形D互为对边综合误差之和与差

表6.9　图形D互为对边双差和方程之和与差

又例如:

余类推，从表6.5中可以直接看出:(www.daowen.com)

又例如:

前者两个数值均为69.7205，后者两个数值均为48.1607，但正负相反，因此可以推论:

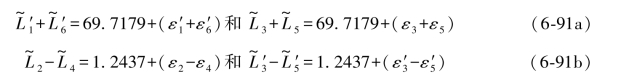
不再一一列举，而这些公式再次证明是和表3.9中的关系式是一致的，而表3.9中的公式，则是通过混合向量导出的。

表6.7中的综合误差公式实际上就是表1.2中的公式，但表6.7中是按对边分组的形式写出的。这样对于求两个综合误差的和与差就可以一目了然。

表6.8中的互为对边综合误差之和与差就是从表6.7中得到的，因为当某两个互为对边的高差真值均为已知时，例如，1边和6边的高差真值均为已知时，此时列出的双差和方程就应该是以下形式:

因此，求两个双差和方程之和或差，就相当于求其综合误差之和与差，这样就可以直接引用表中的结果。

从以上各表中可以看出，任何一个典型图形，它们的原观测向量与其再生向量之间形成了一个环环相扣的数据链。解题的最终目的就是要解开这一数据链。但是必须指出，因为有了上述各表中所表达的数据链，对于解题能够起到关键性的作用，同时也必须注意，由于是环环相扣，只要有一个数据链的数据被误判，例如，(ε3+ε5)＝0.1，而被误判成0.2，0.3，…，则由此就使整个数值的解产生连环性、系统性的误判，这一点正是解题中的一大难点。因此，为了求得正确解，就必须从不同角度予以分析和验证，才能保证得到正确解。