双环条件与再生双环条件数值关系解析

以图形D为例，该图形的原观测向量、再生观测向量及误差距向量为(表1.1):

由以上两式即可分别列出3个双环条件和再生双环条件。如果只列出其中包含有ε1和ε6的两个双环条件为例，则有

从以上两组等式很容易发现，即双环条件及其相应的再生双环条件的4个数值，处于对角线上的两个数值总是数值相等，但正负相反。例如，在第一组等式中，

在第二组等式中，

将上式与(6-38)式相对比，即可得到以下几点结论:

①双环条件方程及其再生双环条件方程所产生的4个数值，处于对角线两端的数值总是数值相等而正负相反。例如，在(6-38)式中，前者为(-2.5)与(2.5)，(0.1)与(-0.1)；后者为(4.9)与(-4.9)，(0.3)与(-0.3)，而在(6-42)式中，前者为(-3.7)与(3.7)，(0.1)与(-0.1)；后者为(3.7)与(-3.7)，(0.3)与(-0.3)

对照(1-20)式知，上式中的-(ε3+ε5)+(ε2+ε4)＝(1)，故有2ε1+(1)＝2.0。同样，如果将(6-37a)中的两式相减即可得到:

对照(1-20)式知，上式中的-(ε3+ε5)-(ε2+ε4)＝(6)，故有2ε6+(6)＝-7.2。

在上面已经讨论过(ε2+ε4)或(ε3+ε5)都是处于数值保持不变的对角线上，无论L1或L6怎样变化，也就是说不管ε1和ε6怎样改变，都不会影响到(ε2+ε4)或(ε3+ε5)，由此得出结论，任意一个观测值Li的改变只影响其本身真误差，但不会影响到它综合误差(i)的大小。

从表3.6中可以查到上述公式中的有关εi和，并代入上式，则有:

以及

将(6-40)中的两式相加，即可得双差和方程为:

两式相减即得:

(https://www.daowen.com)

如果将(6-41)中的两式相加和相减即可得到相应的再生双差和方程为:

以上通过1边和6边的双环条件和再生双环条件讨论了它们之间的数值关系。从(6-38)、(6-42)、(6-46)诸式可以看出，它们之间总是形成4个数值点和两个对角交叉线，其中一个对角线两端的数值是相等、正负相反，且是恒定不变的，另一个对角线的两端的数值也是相等正负相反，但其数值的大小是随ε1和ε6的取值不同而在改变。因此，可以用图6.1概括地表达它们之间的关系。

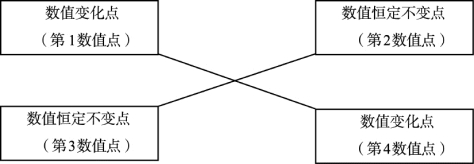
图6.1　双环条件及再生双环条件4个数值点之间的关系图

将表中有关的εi和数值代入(6-48a)式和(6-48b)式可得:

以及

以及

将表中有关的εi和数值代入上式可得:

以及

将表3.3中有关的εi和数值代入上式，则有

将表3.5中的有关εi和的数值代入上式，则有

以及

上述结论与表4.1中所列条件仍然一致。