在每个典型图形中都有3个双环条件，以图形D为例，它的3个双环条件为(见表1.1):

所有双环条件都具有这样一个特点，那就是在每个条件中都包含着两组互为对边的真误差。以上3个双环条件，如果按对边分组的形式书写，就可以写成如下形式:

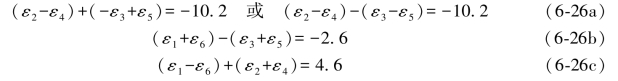
利用(6-26)式中的3个双环条件相加或相减就可以得到6个双差和方程。例如，取(6-26b)与(6-26c)两式相加或相减，即

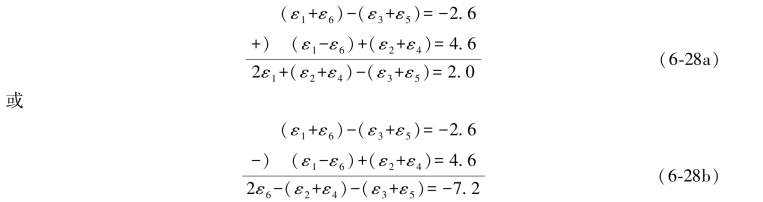
对照(1-20)式可知，(6-28a)式中的(ε2+ε4)-(ε3+ε5)＝(1)，(6-28b)式中的-(ε2+ε4)-(ε3+ε5)＝(6)，所以(6-28a)和(6-28b)两式就可以写成:

同样地，取(6-26c)和(6-26a)两式相加或相减，并将(6-26c)式中的(ε2+ε4)移到前面，则有

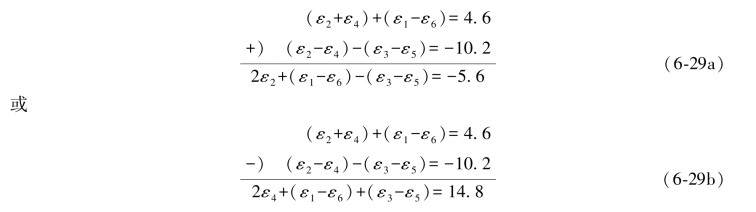
对照(1-20)式知，(6-29a)式中的(ε1-ε6)-(ε3-ε5)＝(2)，(6-29b)式中的(ε1-ε6)+(ε3-ε5)＝(4)，所以(6-29a)和(6-29b)两式可以写成:

(www.daowen.com)

类似地，取(6-26b)式和(6-26a)式相加或相减，为明显清晰起见，分别将两式中的(ε3+ε5)和(ε3-ε5)都移到式子的首项，并适当变动式中的正负号，于是有

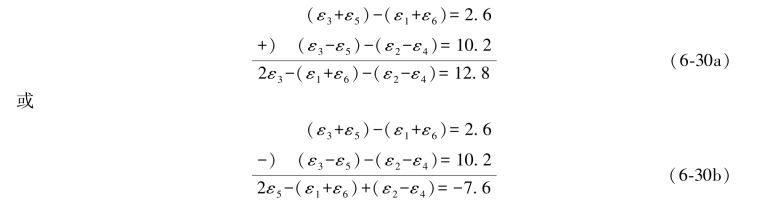
对照(1-20)式知，(6-30a)式中的-(ε1+ε6)-(ε2-ε4)＝(3)，(6-30b)式中的-(ε1+ε6)+(ε2-ε4)＝(5)，所以由(6-30a)式和(6-30b)式可以得到:

表6.4　图形D中3个双环条件的书写顺序

续表

从表3.6中可以查到，当ε6等于零时，则(6-26b)式和(6-26c)式变成如下形式: