对于地面任意两点之间的高差而言，必然有它的一个真值，因为任何一个高差，既不可能没有真值，也不可能同时存在两个或两个以上的真值，尽管真值是未知的，但它是客观存在的。

仍以图形D为例。在表1.1中已经给出了它的真值向量、原观测值向量、再生观测值向量以及它们的真误差向量等，即

从表1.1中还可以查到图形D的4个单环条件和再生条件方程分别为:

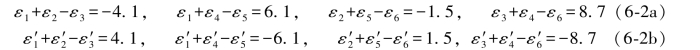
(6-1a)式中的真值虽然是未知的，但是却通过条件方程的闭合差真实而精确地反映了真值与各观测值之间的关系，例如:

为了便于往后查阅，现将上述结果汇集于表6.1中。

表6.1　图形D互为对边的伴随误差值及再生误差值

续表

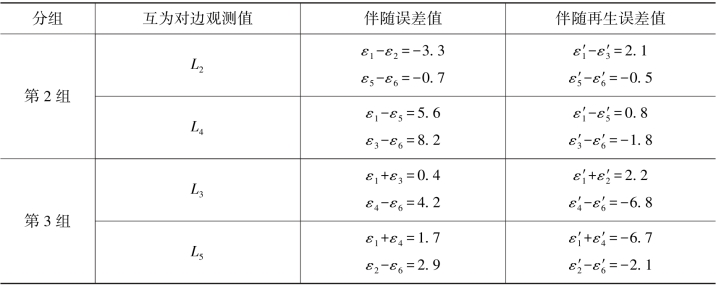
这里很自然会产生一个疑问，在上面求得各个观测值的伴随误差值和再生误差值时，是在各高差真值为已知的情况下求得的，而事实上，尽管高差真值是客观存在的，但是它的具体数值是未知的，因此表6.1中的数值在理论上是存在的，可是实际中是难以求出的，这一疑问将在下面的叙述中得到解决。

由(6-7a)式列出4个单环条件方程为:

对照(3-47d)式，则(6-8a)式的误差矩阵应为:

由(6-8a)式列出4个单环条件方程为:

(6-7a)式是由(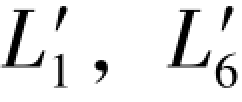)的“一次再生向量”改变而成的一个双真()向量，由该向量列出的条件方程，其闭合差依次是4.9，-5.3，5.0和-5.2(见(6-7c)式)，对照表6.1知，这4个数值正好就是L1和L6的伴随误差值，即

顾及(3-53d)式，则上述向量的误差矩阵应为:

由(6-12a)式列出其单环条件方程如下:

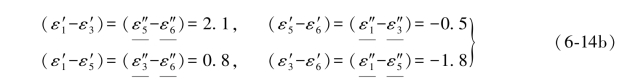
L3和L5的伴随误差值为:(www.daowen.com)

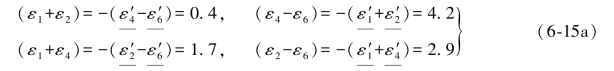
L3和L5的伴随再生误差值为:

通过以上的讨论和分析，可以得到以下几点结论:

①一个典型图形6条边上的高差都有各自的真值，真值是未知的，但是客观上是存在的，一个高差既不可能没有真值，也不可能同时存在两个或两个以上的真值。

②通过水准测量取得6个高差观测值，有了这6个原观测值，不仅可以计算出它的再生观测向量，而且还可以按互为对边的观测值分别组成混合向量或混合再生向量，并进而计算出它们的一次再生向量和二次再生向量，所有这些由原观测向量衍生出来的各种向量，只要原观测值不再修改和变动，所有不同向量中的每个数值也都固定不变了。

③通过条件方程的闭合差真实而精确地反映了所有观测向量与其真值向量之间的关系，特别是一次再生向量和二次再生向量，正如在(6-9)式、(6-14)式和(6-15)式中所显示的那样。它们的真误差精确地反映了每个高差观测值的伴随误差值和伴随再生误差值。这就表明，尽管高差真值是未知的，但它们是有解的，而且是唯一解，换句话说，不存在有多解的问题。

为了方便查阅，现将以上推导的结果汇列于表6.2中。

表6.2　图形D一次、二次再生误差与伴随误差的关系

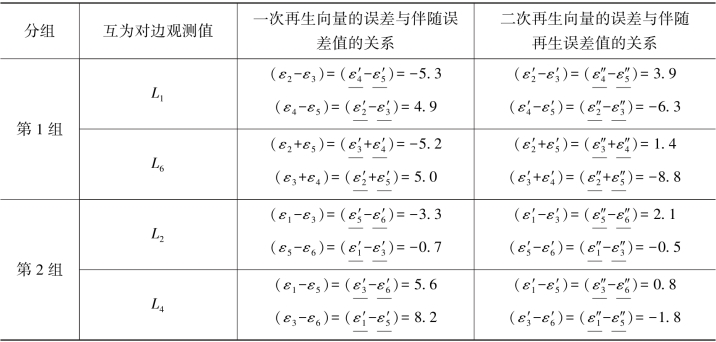
续表

在每个典型图形中，除了6个直接测得的原高差观测值Li之外，还可以计算出6个再生观测值；除此之外，为了构建观测值之间不同形式的函数关系，又提出了混合观测向量以及混合再生向量，并由此进一步得到了一次再生向量和二次再生向量，等等，所有这些就为求解高差真值提供了必要的数值依据。但是由于高差真值是未知的，所以各个观测值的真误差只能通过条件方程，包括单环条件、双环条件、混合单环条件、混合双环条件等条件方程闭合差来反映出真误差的数值大小，而这些都是真误差的函数值，并非是各个真误差的本身。为了弥补这一不足，现在再提出平均观测值的概念。以图形D为例，(3-29a)式和(3-29b)式分别是它的原观测向量和再生观测向量。如果将每个高差的原观测值和再生观测值取平均，则有如下平均观测向量:

因为原观测值Li和再生观测值都是固定不变的，所以(6-16)式中的平均值也是固定不变的。现在就将该平均值向量看成是图形D的真值向量，并称之为“名义真值”，很显然，名义真值与真实的真值之间的差数也如(6-17b)式所示。

由(6-16)式中的名义真值和(3-29a)式与(3-29b)式中的原观测值和再生观测值即可算出相应的真误差和再生真误差分别为:

这里需要说明的是，在以上两式中，仍旧沿用符号εi和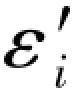分别代表原观测值以及再生观测值与名义真值之间的差数。这和它们与实际真值之间的差数所用的符号没有区分，这主要是因为只有与名义真值才能求出真误差的具体数值，而与实际真值之间的差数只能用符号εi或来表示，一般情况下，是不可能写出真误差的具体数值的。因此，以后只要是用具体数值写出的误差向量，肯定是针对名义真值而言的，而用符号写出的真误差向量，则是针对实际真值而言的。

顾及(6-17a)式，则有

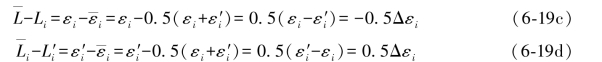
上式中Δεi即为图形D中各个观测值的误差距，由表1.1知，Δε1＝-1.0，Δε2＝2.8，…，Δε6＝3.6，代入(6-19c)式即可得到(6-17c)式中的数值，代入(6-19a)式即可得到(6-17d)式中的数值。不难看出，(6-17c)式中的各个误差值均等于相应误差距的二分之一且反号，而(6-17c)式中的各个再生误差值则等于相应误差距的二分之一且同号。

如果将(6-17b)中的平均真误差分别与(6-17d)中各对应的真误差相减，则有如下结果:

同样，分别与(6-17d)中各再生真误差相加，则有

对照表1.1即可看出，以上两组数值就是图形D中各观测值相对于实际真值之真误差与再生真误差。由此即可写出如下关系式:

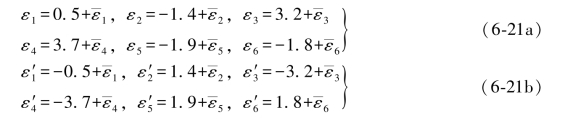
式中，εi和是各观测值相对于实际真值的真误差，而是各观测值相对于名义真值(即平均观测值)的真误差，这样就相当于将一个真误差分成两个误差之和，其中一个数值是已知的，另一个是未知的，但它们的条件方程闭合差(包括单环和双环条件)恒等于零。